EVEN GENERATION of PARETO SET in MULTIOBJECTIVE OPTIMIZATION
The
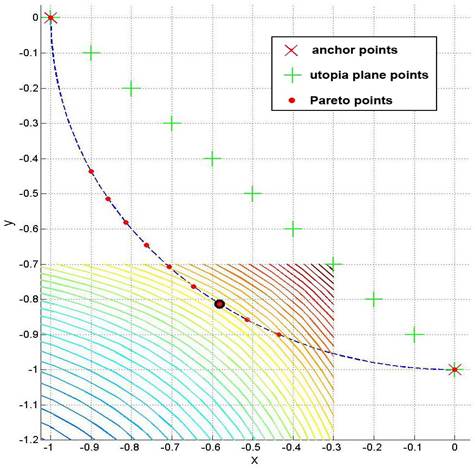
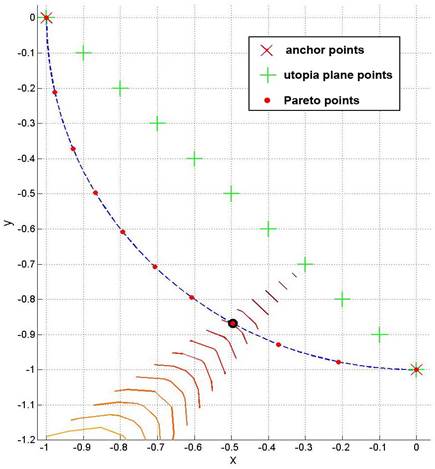
Directed Search Domain (DSD) approach has been developed to generate a well
distributed Pareto set. The method proved to be quite universal.
|
|
Physical
Programming Approach
|
DSD Method
|
1. Utyuzhnikov,
S.V., Guenov, M.D., and Fantini, P., “Numerical method for generating the entire
Pareto frontier in multiobjective optimization”,
Proceedings of EUROGEN 2005, Munich, September 12-14, 2005 (ISBN:
3-00-017534-2).
2. Guenov,
M.D., Utyuzhnikov, S.V., and Fantini, P., “Application of the modified physical
programming method to generating the entire Pareto frontier in multiobjective optimization”, Proceedings of EUROGEN 2005, Munich, September 12-14, 2005 (ISBN:
3-00-017534-2).
3. Utyuzhnikov,
S V, Fantini P, Guenov M.,
"A Method for Generating a Well-Distributed Pareto Set in Nonlinear Multiobjective Optimization", J. Computational and Applied Mathematics, 2009, 223 (2): 820-841.
4. Utyuzhnikov,
S.V., “Multi-Objective Optimization: Quasi-Even Generation of Pareto Frontier
and its Local Approximation”, in “Handbook of Optimization Theory: Decision
Analysis and Application”, Eds: Varela, J., Acuna,
S., Nova Science Publishers, NY, ISBN: 978-1-60876-500-3, 2010.
5. Erfani,
T., and Utyuzhnikov, S.V., “Directed Search Domain: a
method for even generation of Pareto frontier in Multiobjective
Optimization”, J. Engineering
Optimization, 2011, 43
(5): 467-484.
6.
Wang, K., Utyuzhnikov,
S.V., “An extension of the Directed Search Domain algorithm to bilevel optimization”, J.
Engineering Optimization, 2017, 49 (8): 1420-1440.
7. Wang, K., Utyuzhnikov, S.V., "A modified rotation strategy for
directed search domain algorithm in multiobjective
engineering optimization", J.
Structural and Multidisciplinary Optimization, 2018, 57 (2): 877-890.
Sensitivity Analysis is considered in
1. Utyuzhnikov, S.V., Maginot, J., and Guenov,
M.D., “Local Pareto
approximation for multi-objective optimization”, J. of Engineering
Optimization, 2008, 40 (9): 821-847.
For the first time, the linear and quadratic approximations of a
smooth enough Pareto surface have been obtained. It has been proven that the
linear approximation known in the literature is not applicable in the general n-dimensional case.
Robust design in MOO under uncertainties is considered in
1. Erfani,
T., and Utyuzhnikov, S.V., “Control of robust design in multiobjective optimization under uncertainties”, J. Structural and Multidisciplinary
Optimization, 2012,
45 (2): 247-256.
In this paper, trade-off between robustness and Pareto
optimality is addressed.
Ranking in MOO
1. Jaini, N.I., Utyuzhnikov, S.V., “Trade-off Ranking Method for
Multi-Criteria Decision Analysis”, J. Multi-Criteria Decision Analysis, 2017,
24 (3-4): 121-132.

