Why Zero is so Hard
The post on herd immunity on this blog discussed mitigation policies. Since then, the world has moved on somewhat, and many people are talking about long-term suppression of COVID-19, so how long might that take?
Suppose we have \(N\) current COVID infections, the reproduction number is \(R\), the duration of infection is \(T\) and we want to know the time \(t\) until the probability that there are zero cases is \(p\).
If we model this as a Markovian birth-death chain, then the analytical result for the time at which the given probability of extinction is reached is: \[t(p,N,R) = \frac{T}{R-1} \ln\left( \frac{p^{1/N} - 1}{R p^{1/N} - 1}\right) \; . \]
Results from this equation are shown in the Figure if we take 10 days from infection to recovery; unfortunately, we need years with the reproduction number less than one to get appreciable probabilities of of extinction. Of course, the Markovian birth-death chain is too simple to be a realistic model of COVID. In particular:
More infection happens several days after infection than in the initial days, introducing additional delays;
Some population subgroups may have an effective reproduction number above 1;
There will be imported cases from outside;
There is variability in individual susceptibility and infectiousness;
Contact patterns are complex and heterogeneous.
These will influence the time to zero cases in different ways; but the 'inconvenient truth' is that it takes an extremely long time to get to zero cases even if \(R\) can be kept below one indefinitely.
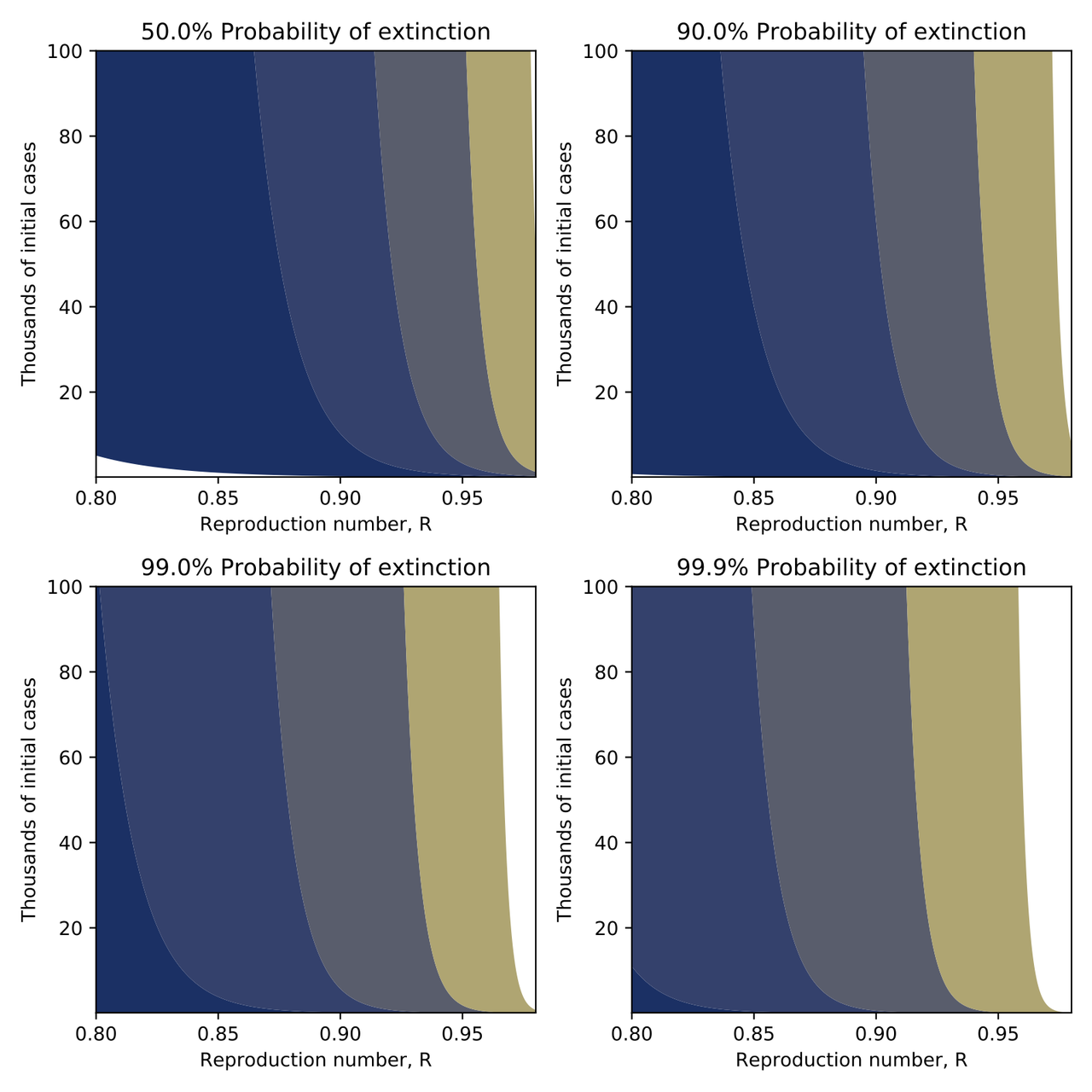
Times until the a given probability of extinction as a function of the initial number of cases and the reproduction number. Contour lines correspond to 1, 2, 3, 5 and 10 years.