6.1 Combining sounds across frequency (octave and 1/3rd octave measurements)

When using sound level meters the levels are often measured in terms of the sound level within a particular octave or 1/3rd octave band. It may be that the sound actually has a spectrum that spans several such bands. For example one filter centered at 500Hz may show a reading of 65 dB SPL, the adjacent octave band centered at 1000Hz may show 70 dB SPL and the 2000Hz band show 68 dB SPL. The question is, how do we find the total sound level.?

We can use the same procedure as described previously to add the actual sound intensities and then convert back to dB SPL. So using equation (5.3) we have:

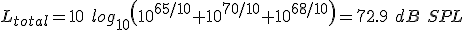
6.2 Combining sounds across frequency (spectrum level)

If we have sound with a relatively broad bandwidth and with a flat spectrum (e.g. bandpass filtered white noise) another way of thinking about the spectrum is in terms of how many bands, each of one Hz wide, make up the spectrum. So for example, if we have white noise that is band pass filtered between 500Hz and 1500Hz then there are 1000 individual bands of noise - each 1 Hz wide that make up the total noise. If the sound level in each of these 1Hz bands is 30 dB SPL, then we can uses what we have learned previously to calculate the total noise level. We refer to the sound level in each 1Hz wide band as the spectrum level of the noise.

So in this example we have L_spectrum = 30dB SPL and a bandwidth of 1000Hz. So to work out the total sound level we have to convert the spectrum level to the intensity within each band and then multiply this by 1000 to give the total intensity (I_total).

First we need to use equation (5.1) to calculate the intensity within the 1Hz bands from the spectrum level:

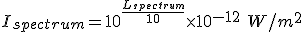(6.1)

We also need an expression for the total intensity:

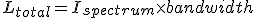   (6.2)

Eq. 6.2 can be expressed in dB to give the overall level:

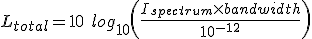(6.3)

If we combine the first and third of these equations we can see that the reference intensities cancel out to make things simpler:

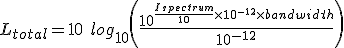
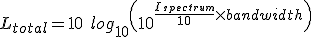
But as we learned in chapter if we take the multiplication outside the brackets it becomes the equivalent of adding two logarithms so this can be further simplified to:

L_total = 10 log₁₀ (I_spectrum)+10 log₁₀ (bandwidth) 

 We now have an equation that relates the spectrum level of the noise to the total sound level.

So if spectrum level = 30 dB SPL and the bandwidth = 1000Hz then the total sound level is given by:

L_total = 30 + 10 log₁₀ (1000) = 60 dB SPL

Similarly, if we know the total sound level we can use equation (6.4) to calculate the spectrum level (assuming that the spectrum is flat).