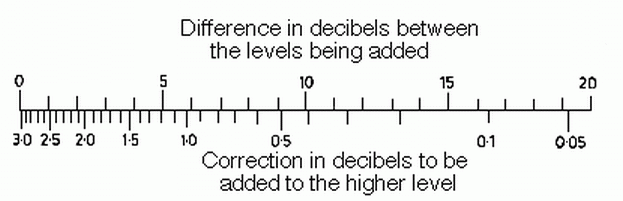
5.2 Adding two equal sound intensities
So, for example suppose we have two independent sound sources producing white-noise and the sound pressure level of each one measured on it's own is 80 dB SPL - our question is, what is the resulting sound pressure level when they are both turned on together?
If we assume that the value in dB SPL is the same as it would be if we measured it in dB IL (i.e. assumptions of a plane wave) then the first thing we need to do is convert our dB SPLs into intensities as in 5.1. (see Example 1). If we refer to the two sound intensities as I1 and I2 which are both equal, then as we have already seen: I1 = I2 = 10-4 W/m2
If we now add I1 and I2 to give Itotal we have:
Itotal = I1 + I2 = 10-4 + 10-4=2 x 10-4 W/m2
So we now have the sound intensity of our combined signal and we can now convert this back to a dB value:
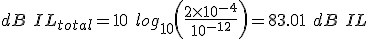
Now since we are talking about plane waves, our total sould pressure level = 83.01 dB SPL.
This example gives us a simple rule:
If we add two unrelated sounds of the same intensity together,
it is equivalent to a 3 dB increase in the total sound pressure level.
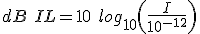
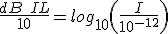
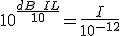
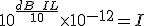 (5.1)
(5.1)
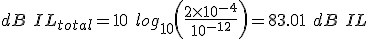
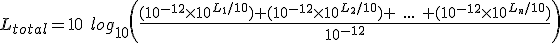 (5.2)
(5.2)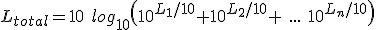 (5.3)
(5.3)