1. What is a Logarithm

If we think of a number, say 10 000 000 then we can represent this number in several different ways - we can use the standard format as we just have done. Alternatively we could use scientific notation 1.0 x 10⁷ which simply means 1.0 multiplied by 10 million. The advantage of scientific notion is that we can represent very large or very small numbers without worrying about miscounting the number of zeroes or decimal places. This is how most calculators represent very large or very small numbers.

Another way of expressing the same number is by saying it is the same as 10 raised to the power of a certain value. For this example, 10000000 = 10⁷. In this example the 10 is referred to as the base, and the 7 is refereed to as the exponent.

This example is relatively straight forward, but we can extend it to use exponents that aren't necessarily whole numbers e.g. 0.005 = 10^-2.301 [use your calculator to demonstrate that this is the case]. Here we have a negative exponent because our number is less than 1.0 (but > 0 - see below). [note, 1 = 1⁰].

A logarithm is simply the value of the exponent on its own. So for example the logarithm (base 10) of 0.005 is -2.301. Similarly the logarithm of 10 million is 7. We usually express logarithms of a number x as log(x) which refers to the "logarithm to the base 10" - this is the "log" button on your calculator. You may also see log₁₀(x) which means the same thing but explicitly states what the base is.

2. Antilogs

if we have a logarithmic value (i.e. the exponent value) we can take the reverse the process by simply raising 10 to the power of that exponent. So for example if log₁₀(x) = -2.301 then x = 10^-2.301 = 0.005

So more generally: if y = log₁₀(x) then x = 10^y

3. Multiplication, division and logarithms

If we have a simple example where we want to multiply 10000 by 100 we get 1000 000. If we write these three in exponent form we have:

104x 102 = 106

i.e. In order to multiply these numbers we simply need to add the exponents. We can extend this further to show how we can use logarithms in the multiplication of two numbers.

Suppose we have two numbers A and B, we can represent both of these in exponent form: A=10^log(A) and B=10^log(B) if we want to multiply these two:

A x B = 10log(A) x 10log(B) = 10log(A)+log(B)

More generally we can write:

log(A x B) = log(A) + log(B)

(1.1)

We can follow similar arguments if we want to divide two numbers A and B:

Or more generally:

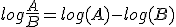
(1.2)

 

 

4. Why do we need logarithms?

There are several reasons why we use logarithms in audiology/acoustics. Here are a few of them:

1. logarithms allow us to deal with very large or small number relatively easily
2. The ear responds to changes of sound intensity in a nonlinear manner - just noticeable changes in sound intensity for loud sounds involves much bigger changes in sound pressure than for quite sounds (i.e. perception of sound intensity is more like a logarithmic scale)
3. The perception of sound frequency (pitch) occurs on a logarithmic scale - e.g. an increase in pitch of one octave involves a twofold increase in frequency.

5. Basic rules of logarithms

As well as the rules for multiplication and division given above, there are various other important rules to remember:

1. The logarithm of 1 is zero.
2. The logarithm of 0 is not possible - it is not possible to raise 10 to the power of a value and obtain 0.
3. Similarly, it is not possible to take the logarithm of negative numbers.
4. The logarithm of a number less than one (but > 0) is negative and the logarithm of a number greater than 1 is positive.
5. Adding two value is NOT the same as adding their logarithms.

6. Some useful values

While logarithms can easily be obtained on calculators, there are various values that are useful to remember:

Number	Log10(Number)
1.0	0
2.0	0.3010
3.0	0.4771
4.0	0.6021
10	1.0

Note, if we know that log(2.0) = 0.3010, we can easily obtain log(20) since 2=10x2, and thus we can use equation (1.1) :

log10(20) = log10(10 x 2) = log10(10) + log10(2) = 1+ 0.3010 = 1.3010

We can use the same method to find the logarithm of 0.2, try that for yourself.