4.1 Spread of sound energy in the freefield

When we are thinking of a sound source in a free-field (i.e. nothing for the sound to hit as it travels away from the source) we can think of the sound waves as expanding like the surface of a balloon being blown up. As it travels outwards the surface of the balloon gets bigger and bigger - the sound energy is spread out over a larger and larger area. As the radius of the balloon doubles, the area goes up four-fold. Remember, the area of a sphere is given by:

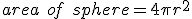(4.1)

So if r goes up by a factor of 2, then the area increases by a factor of 2² or 4. This is demonstrated in figure 4.1 below.

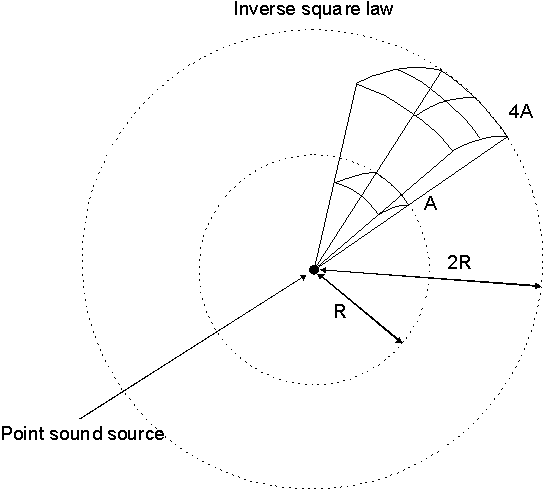
Fig. 4.1: From a point source in free-field sound radiates outwards in all directions. We assume that at a given (R) from the source a certain amount of sound energy flows through area (A). If we now double the distance from the source, the same amount of energy now flows through an area 4 times the size - i.e. for an area of the same size of A, only a quarter of the sound energy passes through it

4.2 Decibels and the inverse square law

If our original sound source has a power given by P then this is this is spread out over the surface of a sphere, then the expression for sound intensity at a given point on that sphere becomes:

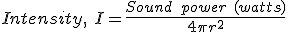(4.2)

So for example, if we have a sound source with a power of 1 W, we measure the intensity at 0.5m from the source and then measure again at a distance of 1m. How much does the sound intensity level drop between the two measurements.

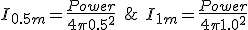
Remember from (3.7) that the ratio of two intensities can be expressed as:

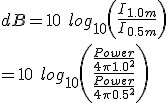
The expression within the brackets can be rearranged - if you want to divide by a fraction you can turn it upside down and multiply by it, then we can simplify:

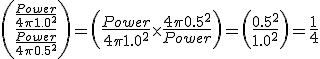
We might have expected this, we have the same sound power, but it passes through 4 times the area, so for a given area unit of area the sound intensity must have decreased by a factor of 4.

We can now think of this decrease in sound intensity in terms of decibels:

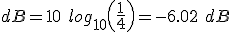
So what does this mean in real life? Basically, if we are in a situation where the inverse square law is obeyed, as we double the distance from a sound source, the sound intensity decreases by 6 dB. This is referred to as the inverse square law.