When we discuss sound we use terms like sound energy, sound power, sound intensity and sound pressure. These are essential to our understanding, but are often confused. Here we will give a brief [non-technical!] description of each.

Sound Energy - Energy is defined as "the ability or capacity of an object to do work". If we think of a single speaker producing sound, as it moves it does work in the process of moving the air molecules around itself - the energy is transfered to the air molecules. Energy is usually denoted by a capital E and the unit of energy is the joule (J).

Sound Power - Power is simply the "rate of expenditure of energy" - that is how much energy is transfered in every second. For our speaker it describes how much energy is expended per second in moving the surrounding air molecules. Power is usually denoted by a capital P, and the unit of power is the watt (W).

Sound Intensity - As the speaker plays a sound, the energy travels out in all directions and as it does so it is spread out over a larger area. Sound intensity refers to the amount of sound energy that passes through a particular area in one second (i.e. power/area). Sound intensity is usually denoted by a capital I and the unit of intensity is W/m² or Wm^-2

Sound Pressure - When the speaker isn't moving the surrounding air will be at atmospheric pressure (with a certain density of molecules). As the speaker moves outwards it applies a force to the air molecule pushing them together (compression), as it moves back it leaves a region of fewer molecules (rarefaction). The moving molecules then collide with adjacent ones and pass on the energy. The sound pressure is simply the amount of force that is applied by the moving molecule per unit area. Sound pressure is usually denotes by a small p, and the unit is the pascal (Pa) where 1Pa = 1 N/m²

The pressure fluctuations in the air that are associated with sound are a result of the air molecules vibrating backwards and forwards. At one point in time they are bunched up together giving a high pressure. At some moment later they are spread out giving a low pressure.

Sound Pressure is measured in Pascals (Pa) - the pressure range to which the human ear is sensitive ranges from approximately 2x10^-5Pa to 200 Pa. These are relatively small values compared to normal atmospheric pressure which is around 10⁵Pa.

Because the human ear (a) responds to sound pressure, (b) responds to a large range of pressures (100 000 000 fold) and (c) responds in a way that is not directly proportional to sound pressure, a logarithmic scale (dB) is used.

Weber suggested that the subjective response (R) is proportional to the fractional change of stimulus (S). i.e.:

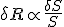(2.1)

Where δS is the change in stimulus and δR is the change in response - Equation 2.1 is an example of Weber's Law

This leads to Fechner's law which states that the actual response will be proportional to the logarithm of of the stimulus:

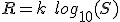(2.2)

In practice, the logarithmic representation of sound pressure we use actually compares one value to another rather than giving and absolute value - i.e. it is a logarithmic ratio of sound pressures referred to as the decibel scale.

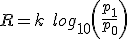(2.3)

That is, the dB scale is simply a comparison of two sound pressures. In practice we usually take p₀ as being a reference value approximating the sound pressure at threshold of hearing - 2x10^-5 Pa. Thus the dB scale now becomes dB sound pressure level, or dB SPL given by:

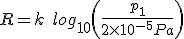(3.4)

When we use a sound level meter (SLM) to measure a sound, the device has a single microphone which responds to sound pressure - the SLM then does the calculation for us and converts the sound pressure measurement into dB SPL.

While measurement of sound pressure is the usual way in which we quantify sound it does not tell us anything about the direction in which the sound is traveling or about the power of a particular sound source. For this we need to measure the sound intensity.

The best way of thinking about the intensity of a sound is to think of a particular sound source that is producing a certain amount of sound energy per second (i.e. a given amount of sound power measures in watts [W]). If this energy is free to flow outwards in all directions then the original energy is spreading out and the amount of energy in a given area decreases. We can quantify the amount of power passing through a given area and we refer to it as the sound intensity (measured in W/m²).

The intensity of a sound is actually proportional to the sound pressure squared i.e. 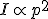In other words,

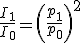(3.5)

If we now think back to equation (3.3), our expression of the ratio of two pressure we can rewrite it to give:

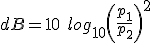(3.6)

Note, the 20 in equation 1.3 has now become a 10 because of the nature of logarithmic relationships [log(x²) = 2log(x)].

So now if we substitute our ratio of intensities into eq. (3.6) we have and equation for dB where intensity (I) is measured in W/m²:

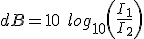(3.7)

3.4 The relationship between dB SPL and dB IL

If we make certain assumptions about the nature of the sound waves (i.e. that they are what are called plane waves) then the intensity is proportional to the square of the pressure divided by a particular characteristic of the air (or whatever medium the sound is traveling in) called the "characteristic acoustic impedance". Basically, this is a measure of how much the air impedes the flow of energy through it.

So, if we apply a pressure (i.e. a particular force applied over a unit of area: 1Pa = 1N/m²), the air impedes the energy flow and the sound intensity (W/m²) is a measure of the resulting energy flow through this unit area in a given time. The amount by which the air impedes the energy flow is given by the "characteristic acoustic impedance" of the air which is given by: ρc where ρ is the density of air and c is the speed of sound in air.

At typical room temperature and air pressure, ρc = 410 rayls. Thus we have an equation relating sound intensity and sound pressure:

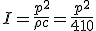(3.8)

Now we already know that in the equation for dB SPL, we have defined the reference pressure according to auditory threshold as 2x10^-5Pa. So we can use this equation (3.8) to define the equivalent reference intensity:

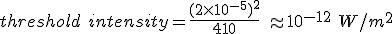
So we can now produce an equation for dB intensity level (dB IL) by putting this value into equation (3.7)

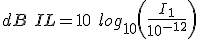  (3.9)