|
|
MEMBRANE TRANSPORT |
MENU
|
MEMBRANE TRANSPORT |
||
|
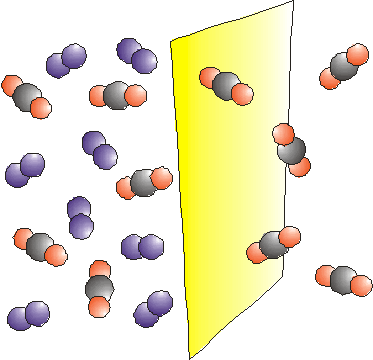
The overall driving force for permeation through a membrane is a gradient in
chemical potential. There are various ways of generating a chemical potential
gradient and hence a driving force for permeation. |
|
|
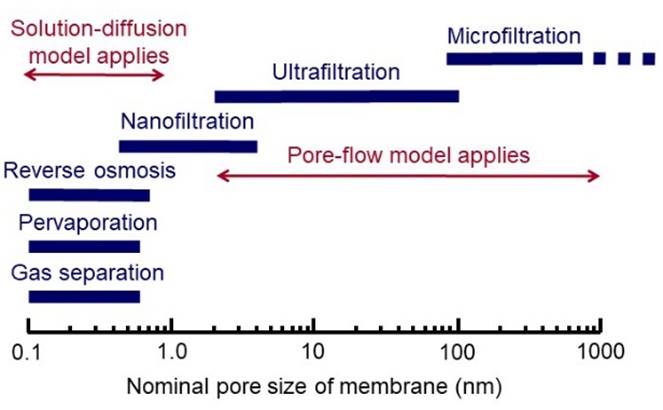
PORE FLOW MODEL In the pore-flow model,
transport of permeating species through a membrane is by pressure-driven flow
through tiny pores. An equation for the flow of a fluid through a porous medium was
proposed in 1856 by the French engineer Henry Darcy. |
|
|
|
If a membrane has pores much larger than the permeating species,
it is usually non-selective. |
|
|
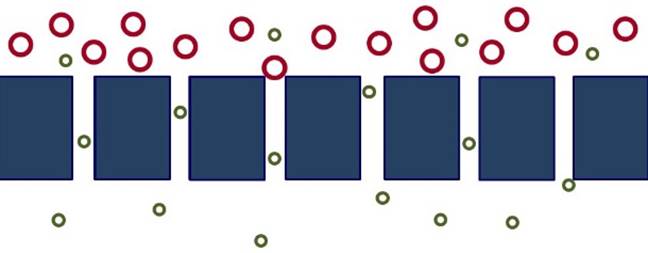
KNUDSEN DIFFUSION Separation of gases
may occur by Knudsen diffusion when
a membrane has pores big enough for the gases to enter, but smaller than their mean free path. |
|
In Knudsen diffusion, gas
molecules collide with the pore walls much more frequently than they collide
with each other. The flux of a species is
inversely proportional to the square root of its molecular mass, so lighter
molecules move across the membrane
faster than heavier molecules. |
|
|
|
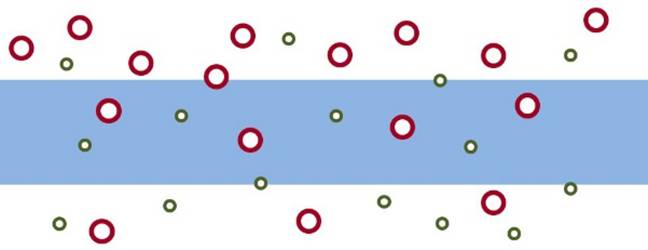
MOLECULAR
SIEVING When a membrane has pores
close in size to the permeating species, separation may occur because one
species is filtered from pores in the membrane through which other species
can move (molecular sieving). |
|
|
SOLUTION-DIFFUSION MODEL Many membranes are made of more or less “dense” materials and transport may be described by a solution-diffusion model. |
|
In the solution-diffusion model it is assumed that permeation
involves: Dissolution or sorption of the permeating species in the
membrane on the feed side. Diffusion through the membrane. Desorption at the permeate side. In the simplest case, diffusion through the membrane can be
described by Fick’s laws. |
|
|
|
|
|
|
|
|
Other forms of membrane transport include facilitated transport,
where a carrier interacts with a specific species to help transport it across
the membrane. Different models are applicable to different membrane processes. |
|
FURTHER READING
R.W. Baker, Membrane Technology and Applications, Third Edition
Wiley, Chichester, 2012. DOI: 10.1002/9781118359686