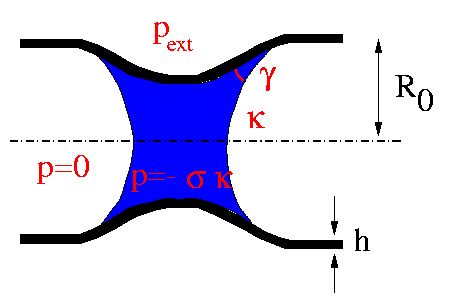

Since we want to model non-axisymmetrically buckled tubes, the real model is slightly more complicated than indicated in the above sketch: We need two sets of surface coordinates to parametrise the tube wall and the meniscus. We also have to parametrise the position of the contact line on the tube wall. The following picture shows how this is done (only one half of the tube and one meniscus need to be modelled since the configuration is symmetric in the axial direction -- we cut the tube in the plane of symmetry at z=0).
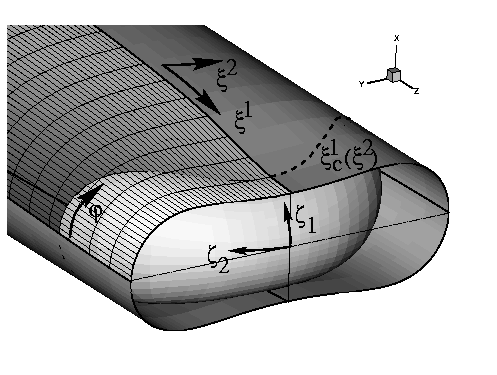
To solve the problem mathematically/computationally, the wall deformation was described by geometrically non-linear shell theory, coupled to a variational description of the meniscus shape. A spine method was used to implement the parametric description of the meniscus shape. The resulting highly non-linear equations were discretised with Finite Element Methods and solved with a global Newton-Raphson method, embedded in an adaptive continuation technique.