Fluid-Structure Interaction Problems:
Flow in Collapsible Tubes
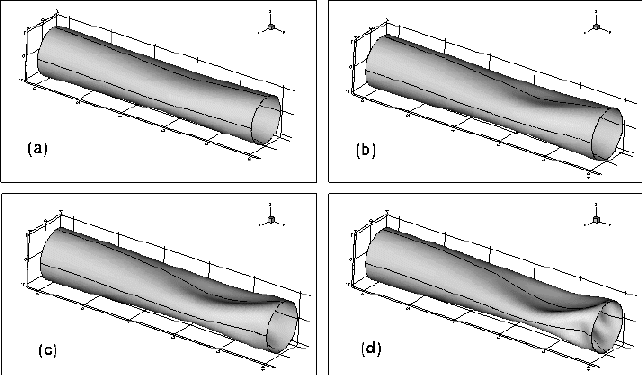
The figure below shows the deformation of a thin-walled elastic tube
which conveys a viscous flow (the direction of the flow is from left
to right). In its undeformed state, the tube is cylindrical and the
ends of the tube are held open (think of a thin-walled rubber tube,
mounted on two rigid tubes).
As we increase the external pressure [from (a) to (d)],
the tube buckles and deforms strongly. The reduction in the tube's cross
sectional area changes its flow resistance and thereby the pressure
distribution in the fluid, which in turn affects the tube's deformation.
This is a classical example for a large-displacement fluid-structure
interaction problem for which many applications exist in biomechanics
(e.g. blood flow in veins and arteries, flow of air in the bronchial
airways).
To model this problem, the wall deformation was described using
geometrically non-linear shell theory, coupled to the
three-dimensional steady Stokes equations (zero Reynolds number flow).
The equations were discretised with
Finite Element Methods and the
coupled solution was achieved with a segregated solver.
Page last modified: July 25, 1997
Back to Matthias Heil's home page..

