Week 9 Exercises — solutions
Version 2025/02/09. These exercises in PDF To other course material
-
Exercise 9.0. An unseen exercise on gluing. Definition: let \(X\) be a top. space, \(Y\) a set (initially without a topology), \(q\colon X \to Y\) a surjective map. The topology on \(Y\) given by
\(V \subseteq Y\) is open in \(Y\) \(\overset {\text {def}}{\iff }\) \(q^{-1}(V)\) is open in \(X\)
is the quotient topology on \(Y\) induced by \(q.\) In this situation, \(q\) is the quotient map.
In particular, if \(\sim \) is an equivalence relation on \(X,\) take \(Y := X/\mathord {\sim }\) to be the set of \(\sim \)-equivalence classes, and define \(q\colon X \to Y\) by \(q(x)=[x].\) The quotient topology on \(X/\mathord {\sim }\) is called the identification topology with respect to \(\sim .\) (Idea: whenever \(x'\sim x'',\) we identify points \(x'\) and \(x''\) and treat them as one point.)
Gluing topology is identification topology where \(\sim \) is such that
-
• some equivalence classes consist of \(2\) points (two points glued together);
-
• the rest of equivalence classes are singletons.
Theorem (universal mapping property for a quotient space). Let \(Y\) be a quotient space via the quotient map \(X \xrightarrow {q} Y.\) Given any topological space \(Z,\) there is a 1-to-1 correspondence between
-
• continuous maps \(f\colon Y\to Z;\)
-
• continuous \(F \colon X \to Z\) such that \(F(x')=F(x'')\) in \(Z\) whenever \(q(x')=q(x'')\) in \(Y.\)
The correspondence is such that \(F =f\circ q .\)
CHALLENGE: construct embeddings, or at least “immersions”, in \(\RR ^3,\) of the gluing spaces given by schematic diagrams presented in class.
-
Answer to E9.0. [These exercises without answers]
Diagram 1:
\(X=[0,1]\) with the points \(0\) and \(1\) glued together.
In more detail, the equivalence relation \(\sim \) on \(X=[0,1]\) is defined by: \(0\sim 1\) so that \([0]=[1]=\{0,1\};\) other equivalence classes are singletons, i.e., \([x]=\{x\}\) \(\forall x\in X\setminus \{0,1\}.\)
Could \([0,1]\) with \(0\) and \(1\) glued together look like this?
Informally, if we try to bend the interval and glue together its endpoints (we need a \(2\)-dimensional to do this!), we get something like a loop. We conjecture that \(X/\mathord {\sim }\) is homeomorphic to the circle. Let us prove this.
Claim 1: If \(X=[0,1]\) and \(\sim \) is the equivalence relation described above (“gluing together \(0\) and \(1\)”), then the quotient space \(X/\mathord {\sim }\) is homeomorphic to the circle \(S^1.\)
Proof: a homeomorphism \(X/\mathord {\sim }\to S^1\) is, in particular, a continuous map. All such continuous maps are described by the universal mapping property for a quotient space: namely, they are the same as continuous maps \(f\colon X \to S^1\) such that \(f(0)=f(1).\)
We view \(S^1\) as the subset \(\{(x,y)\in \RR ^2: x^2+y^2=1\}.\) Put \(f(t) = (\cos 2\pi t,\sin 2\pi t)\) so that \(f(0)=f(1).\) Note that \(f\) has distinct values on all \(\sim \)-equivalence classes so \(f\) is injective on \(X/\mathord {\sim }.\) Clearly, \(f\) is also surjective; \(f\) is continuous because its components, \(\cos 2\pi t\) and \(\sin 2\pi t,\) are continuous functions on \([0,1].\)
Thus, \(f\colon X /\mathord {\sim } \to S^1\) is a continuous bijection. Note that:
-
• \(X=[0,1]\) is compact by the Heine-Borel lemma.
-
• So, \(X/\mathord {\sim }\) is compact as the image of \(X\) under the (continuous) quotient map \(q.\)
-
• \(S^1\) is Hausdorff as it is a metric space.
By Topological Inverse Function Theorem, a continuous bijection \(f\) from a compact to a Hausdorff space is a homeomorphism. We have rigorously proved that the closed interval with its ends glued together is homeomorphic to a circle.
Remark: the space \([0,1]/\mathord {\sim }\) that we have considered can be called “the abstract circle”. We have thus embedded the abstract circle in \(\RR ^2.\)
Diagram 2:
Diagram: In more detail:
The diagram on the left indicates (using colour) that two parallel edges of the square \(X=[0,1]\times [0,1]\) must be glued together. The arrows on the coloured edges, which point in the same direction, specify which point is glued to which: namely, a point at distance \(t\) from the bottom left corner is identified with the point at the same distance \(t\) from the bottom right corner. This is shown in more detail in the diagram on the right.
We try to construct the quotient space informally by bending the square and gluing the edges in \(\RR ^3.\) The figure shows the process of bending the square and gluing the opposite sides to obtain a cylinder. It is also easy to construct a homeomorphism from \(X/\mathord {\sim }\) to the cylinder: writing the cylinder as \(S^1\times [0,1]\subseteq \RR ^3\) and put \(f(t,u) = (\cos 2\pi t, \sin 2\pi t, u)\) where \((t,u)\in [0,1]\times [0,1].\) We omit the proof that \(f\) is a homeomorphism, which is similar to Diagram 1. Thus, Diagram 2 defines a topological space \(X/\mathord {\sim }\) which can be called “the abstract cylinder”, and we have just embedded this space in \(\RR ^3.\)
Bending the square in \(\RR ^3\) to glue its opposite edges together and obtain a cylinder [Link to online interactive 3D diagram]
Diagram 3:
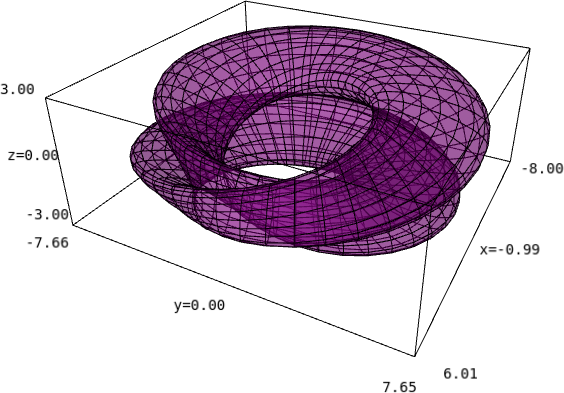
Here we glue together the points \((t,0)\) and \((t,1)\) for all \(t\in [0,1],\) and glue together \((0,u)\) with \((1,u)\) for all \(u\in [0,1],\) of the square \(X=[0,1]\times [0,1].\) The resulting quotient space \(X/\mathord {\sim }\) may be called a “schematic torus”: it is not difficult to show that it is homeomorphic to \(\mathbb T^2 = S^1\times S^1.\)
Informally, the torus embedded in \(\RR ^3\) can be obtained by stretching and bending the cylinder obtained above in order to glue the two circular edges together, see Figure.
Bending the cylinder to glue its circular edges together and obtain a torus [Link to online interactive 3D diagram]
We will now write down an embedding \(f\) of \(X/\mathord {\sim }\) in \(\RR ^3,\) providing explicit formulas for the embedding of \(\mathbb T^2\) in \(\RR ^3\) described in the lectures.
Points \((t,0)\in X\) are mapped onto the circle of radius \(r\) centred at \((R,0,0)\) in the \(xz\) plane: \(f((t,0)) = (R + r\cos 2\pi t, 0, r\sin 2\pi t).\)
Now, \(f((t,u))\) is defined as \(f((t,0))\) rotated around the \(z\) axis through the angle of \(2\pi u.\) Recall that the matrix of such rotation is \(\mathit {Rot}_z(2\pi u)=\begin {pmatrix} \cos 2\pi u & -\sin 2\pi u & 0 \\ \sin 2\pi u & \cos 2\pi u & 0 \\ 0 & 0 & 1\end {pmatrix}.\) We thus have
\(\seteqnumber{0}{9.}{0}\)\begin{align*} f((t,u)) & = \mathit {Rot}_z(2\pi u)f((t,0)) \\ & = \bigl ( (R + r\cos 2\pi t)\cos 2\pi u, (R + r\cos 2\pi t)\sin 2\pi u, r \sin 2\pi t\bigr ). \end{align*} The function \(f\) “respects” gluing, i.e., takes the same value on \((t,0)\) and \((t,1),\) similarly for \((0,u)\) and \((1,u).\) Hence \(f\) gives a well-defined function \(X/\mathord {\sim }\to \RR ^3.\) As long as \(R>r,\) the function \(f\) is injective on \(X/\mathord {\sim },\) which is compact. Applying the Topological Inverse Function Theorem as we did earlier, we conclude that \(f\) is an embedding.
The image of \(f\) is the familiar “surface of a doughnut” [Link to online interactive 3D diagram]
Diagram 4:
Attention! The arrows tell us that on the horizontal edges, we glue together the points \((t,0)\) and \((1-t,1)\) for all \(t\in [0,1].\) The quotient space \(X/\mathord {\sim }\) is the “schematic Klein bottle”. One can prove (which is beyond the scope of our course) that \(X/\mathord {\sim }\) is not embeddable in \(\RR ^3.\)
One can construct a function \(f\colon X \to \RR ^3\) which glues together the points identified by \(\sim \) but also some other points. The resulting continuous map \(X/\mathord {\sim } \to \RR ^3\) is usually called an immersion.
An explicit formula for \(f\colon X \to \RR ^3\) can be as follows: writing \(\varphi = 2\pi t,\) \(\theta =2\pi u,\)
\(\seteqnumber{0}{9.}{0}\)\begin{align*} f(t,u) = \Bigl ( & (R + \cos \frac \theta 2 \sin \varphi - \sin \frac \theta 2 \sin 2\varphi ) \cos \theta \Bigr ., \\ & \bigl .(R + \cos \frac \theta 2 \sin \varphi - \sin \frac \theta 2 \sin 2\varphi )\sin \theta \bigr ., \\ \Bigl .&\sin \frac \theta 2 \sin \varphi + \cos \frac \theta 2 \sin 2\varphi \Bigr ). \end{align*} It is easy to verify that \(f\) respects gluing: \(f(0,u)=(R \cos \theta , R\sin \theta , 0) = f(1,u)\) and also \(f(t,0) = (R+\sin \varphi , 0, \sin 2\varphi )\) equals \(f(1-t,1) = (R-\sin (2\pi -\varphi ), 0, -\sin (4\pi -2\varphi )).\) However, \(f\) also glues the line \(t=\frac 12\) to the line \(t=0\) (and \(t=1\)). The resulting 3d surface, a “symmetric” immersion of the Klein bottle in \(\RR ^3,\) is as shown in the Figure.
References for the exercise sheet
Quotient spaces and surfaces are discussed in [Sutherland, Chapter 15], which includes proofs of the theoretical results given above and the embedding of the torus in \(\RR ^3\) which we considered here. The Klein bottle immersions in \(\RR ^3\) are discussed in popular topology resources (see this example). The images of the “surface of a doughnut” and the “bagel-like” Klein bottle were generated by 3d plotting in SageMath computer algebra system. The SageMath code for the Klein bottle was generated by OpenAI ChatGPT.
Version 2025/02/09. These exercises in PDF To other course material