If a catalyst particle is porous then the reactant will move into the particle as it reacts and thus the internal mass transfer is important. The video below reviews a mole balance in spherical coordinates and then shows how this can be used to calculate the concentration profile though the particle.
The concentration profile inside the particle is dependent on the dimensionless parameter $\Phi$. The parameter is known as the Thiele Modulus. The full derivation of the concentration profile can be seen in this document.
The graph below gives an example of the concentration profile through the catalyst particle at different values of the Thiele modulus, which can be varied with the slider. The right hand side of the graph is the outside of the particle and the left hand side is the centre of the particle. At low values of the Thiele modulus the surface reaction is rate limiting and thus the concentration in the pores is equal to that at the outside of the particle. At high values of the Thiele modulus the internal diffusion is rate limiting and thus the concentration in the pores quickly drops to almost nothing.
As the concentration through the particle varies, the reaction rate varies with position in the particle. This means that it makes sense to define an effectiveness factor, which allows comparision to a single known reaction rate. The video below derives the effectiveness factor for a spherical particle with a first order reaction.
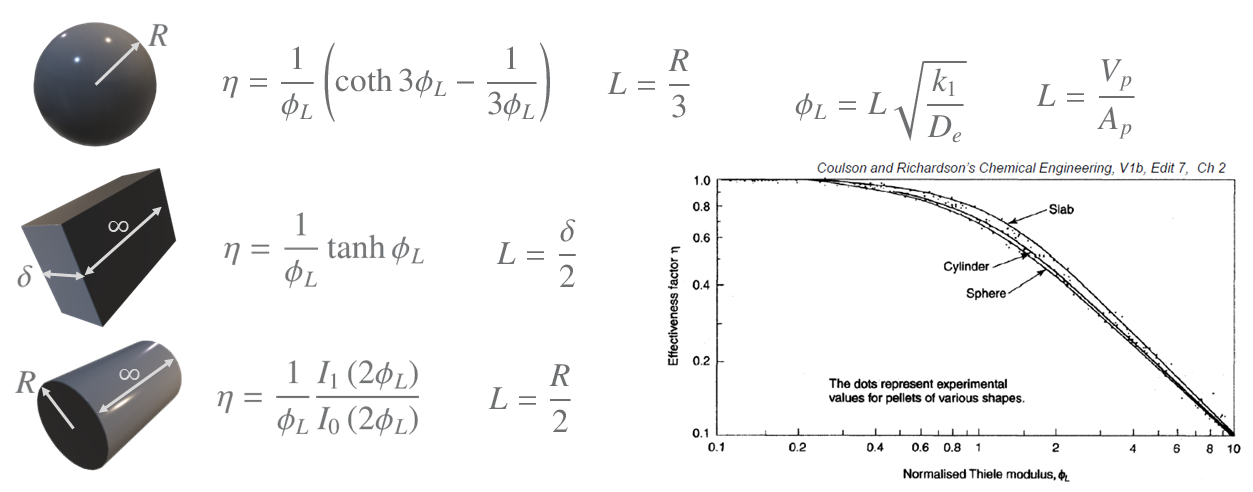
The derivation in the video can also be carried out for other shapes of particles. The derivations for these are complex and thus the results are just given below for 1st order reactions (note the slight difference in the Thiele module used here - which is use to colapse the data). It can be seen that with the normalised Thiele modulus that the results all fall quite closely together, irrespective of the particle shape. The $\eta - \phi_L$ plot is not particularly sensitive to the shape of the particles, and a single curve can be used for most practical applications, particularly at high values of the Thiele modulus where reaction is confined to a thin region close to the surface whose curvature is then unimportant.

$I_1$ and $I_0$ are Bessel functions.
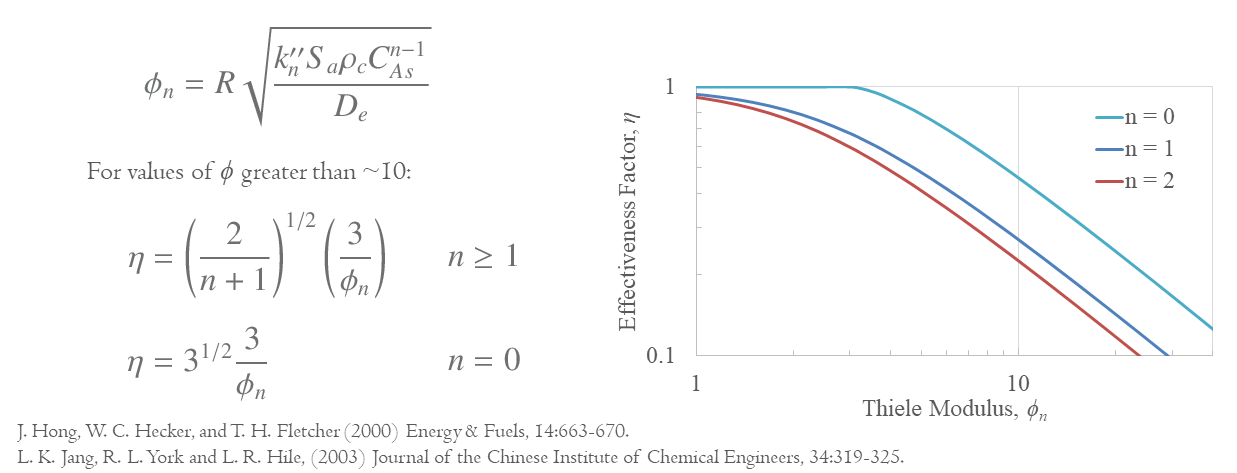
The same process can also be carried out for different orders of reactions for spherical particles. The form of the general expression for the effectiveness factor is very complex, but the approximation for large values of the Thiele modulus (i.e. where there is need to take into account the mass transfer limitation) is quite simple as below,