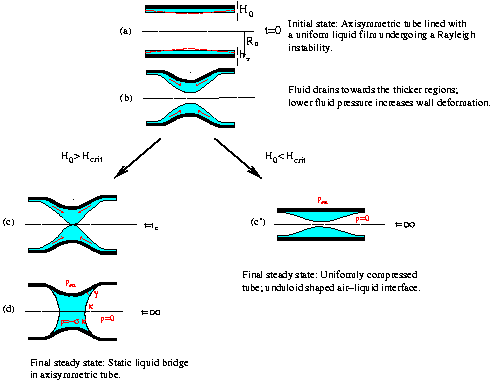
Results
Non-axisymmetric instabilities of liquid-lined elastic rings
The first problem we considered was the development of
non-axisymmetric instabilities of liquid-lined elastic rings.
(This analysis also applies to the case in which a finite length airway
collapses axially uniformly). We performed a linear stability
analysis to establish the value of the external pressure pext
for which an axisymmetric, liquid-lined ring becomes unstable to
non-axisymmetric perturbations. This analysis showed that the ring
will buckle non-axisymmetrically (with a circumferential wavenumber of
N=2) if
pext + sigma 1/(1-H0) > 3.
This result has the simple physical interpretation that buckling
occurs when the compressive load created by the combination of
the external pressure and the surface tension exceeds the classical
buckling pressure, pext(buckl) = 3, of a dry ring.
Numerical simulations (based on a fully coupled finite
element discretisation of the governing equations) were then used
to study the system's evolution following the onset of the
non-axisymmetric instability. These simulations showed that
for sufficiently large surface tension, the strong coupling between
fluid and solid mechanics can induce a catastrophic collapse of the
liquid-lined airway which leads to its complete occlusion.
Fig. 2 illustrates the mechanism responsible for
the collapse: Following the onset of the instability, the ring buckles
non-axisymmetrically and surface tension forces drive fluid into the
buckling lobe. (Surface tension attempts to return the air-liquid
interface to an axisymmetric shape.) During this process, the
curvature of the air-liquid interface
(and hence the compression of the airway wall) increases continuously.
At sufficiently large surface tension, the increase in compression can
become so large that it cannot be balanced by the elastic restoring
forces created by the ring's deformation. This leads to a
rapid reduction of the luminal area and ultimately the complete occlusion of
the airway.
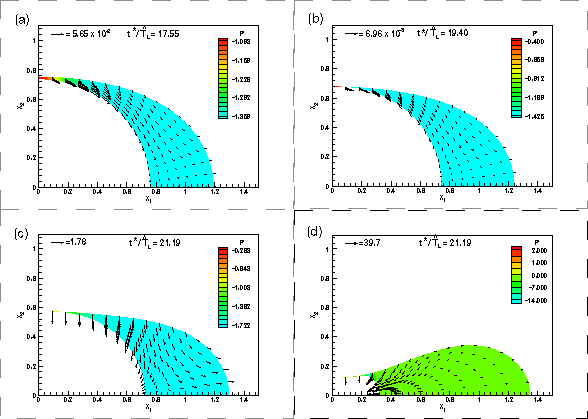
Figure 2: Illustration of the
non-axisymmetric collapse of a
liquid-lined ring: As the ring buckles, the curvature of the
air-liquid interface
increases and the fluid pressure becomes increasingly negative
(see pressure contours). The increase in the wall compression
accelerates the collapse and ultimately the lumen becomes completely
occluded. Note the rapid evolution during the final stages of the
collapse: The transition between (c) and (d) occurs in less than
10-3 dimensionless time-units.
In the simulation presented in Fig. 2 the fluid
flow was computed by (numerically) solving the full 2D Navier-Stokes
equations. The simulation shows that during the final stages of the
airway collapse, the liquid lining becomes very thick. In this regime
lubrication theory can not be expected to (and, in fact, does not)
provide an adequate description of the fluid mechanics. We developed
an improved lubrication theory model, which ensures exact mass
conservation even in situations in which the film has become thick
and the substrate and/or the air-liquid interface have become highly
curved. A detailed comparison with the full Navier-Stokes simulations
showed that, at least in the present application, this model
provides an excellent description of the system's behaviour.
Further details can be found in our paper:
Heil, M. & White, J.P. (2002) Airway Closure: Surface-tension-driven
non-axisymmetric instabilities of liquid-lined elastic rings.
Journal of Fluid Mechanics 462, 79-109. (ps preprint)(abstract)
The linear (in-)stability of the evolving axisymmetric configuration
The analysis discussed in the previous section showed that an airway
can become occluded
via an axially uniform, non-axisymmetric collapse if
the external (pleural) pressure exceeds a critical value.
Next we considered the behaviour of an airway that is initially
lined with a uniform layer of liquid and loaded by an external
(pleural) pressure below this buckling pressure. If the airway
is sufficiently long, the liquid lining is unstable to
the axisymmetric Rayleigh instability. We wished to
investigate if the additional wall compression that is generated when
the liquid lining undergoes the Rayleigh instability can be sufficient
to cause the wall to buckle non-axisymmetrically.
For this purpose, we first developed a numerical scheme to simulate
the axisymmetric evolution of the airway wall and the
air-liquid interface during the Rayleigh instability; typical results are
shown in Fig. 3(a).
The stability of this evolving configuration with respect to
non-axisymmetric perturbations was then determined by a
frozen-coefficient linear stability analysis.
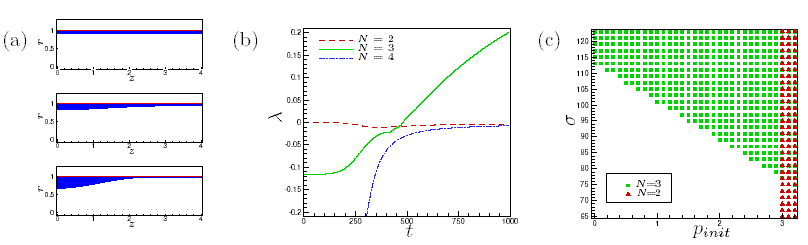
Figure 3: (a)
The axisymmetric wall
and air-liquid interface shapes at t=0 (top), t= 300 (middle),
t=980 (bottom).
(b) The maximum growth rate lambda of the non-axisymmetric
perturbations with wavenumbers N=2,3,4 against non-dimensional time t.
(c) The parameter values pinit, sigma
for which the system becomes unstable to buckling instabilities with
wavenumber N during
the evolution of the axisymmetric Rayleigh lobe.
A representative result is shown in Fig. 3(b)
which plots the growth rates of modes N=2,3,4 (N is the circumferential
wavenumber of the perturbation) as a function of (non-dimensional) time.
At t=0, the growth of the Rayleigh instability is initiated.
During the early stages of the system's evolution, the growth rates
of the non-axisymmetric perturbations are all negative, indicating
that the axisymmetric state is stable. At t = 480, the
growth of the Rayleigh instability has increased the wall compression
so much that the system becomes unstable to non-axisymmetric
perturbations with a circumferential wavenumber of N=3.
We performed a large number of such simulations to map out the
regions in parameter space in which the axisymmetric system becomes unstable
to non-axisymmetric perturbations at some point during its
axisymmetric evolution. An illustrative result is shown
in Fig. 3(c), where a marker
indicates a combination
of the initial wall compression, pinit = pext +
sigma/(1-H0),
and the surface tension sigma for which a non-axisymmetric
instability is predicted to occur. For pinit > 3 the system is
always unstable to the axially uniform instability with wavenumber
N=2, as shown in the previous section. For sufficiently large
surface tension the system can also become unstable
at pinit < 3. In these cases the non-axisymmetric instability
is initiated by the Rayleigh instability.
The system's non-axisymmetric evolution in the
large-displacement regime
Having established that the axisymmetric Rayleigh instability can
initiate the non-axisymmetric buckling of the airway wall, we
proceeded to determine if the nonlinear growth of the instability can
result in the occurrence of airway closure. For this purpose we
developed a numerical scheme for the coupled solution of the
three-dimensional shell and lubrication theory equations.
The simulations were started from an axially uniform configuration
and small axial and circumferential perturbations were applied to
initiate the Rayleigh and buckling instabilities, respectively.
Fig. 4 illustrates the system's evolution for the case
where the axial wavelength L corresponds to the fastest
growing Rayleigh mode. Fig. 4(a) shows the initial
configuration in which a thin liquid film lines the uniform
axisymmetric tube. In Figs. 4(b-c) the redistribution of
liquid by the axisymmetric Rayleigh instability is
clearly visible: The film thickness has increased substantially at one
end of the domain whereas the film has become very thin at the other end.
The increased curvature of the air-liquid interface in the region
where the film thickness has increased, leads to an additional
compression of the airway wall. In Fig. 4(c)
this compression has initiated the buckling of the airway wall. As
the non-axisymmetric collapse proceeds, the air-liquid interface
moves inwards very rapidly, see Fig. 4(d).
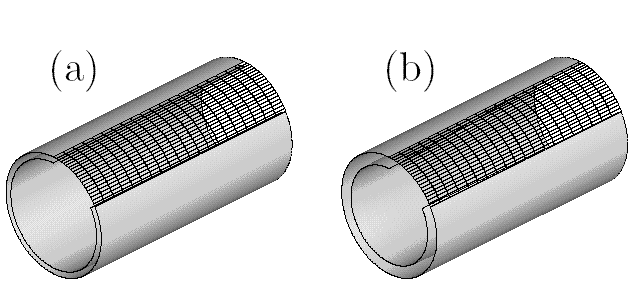
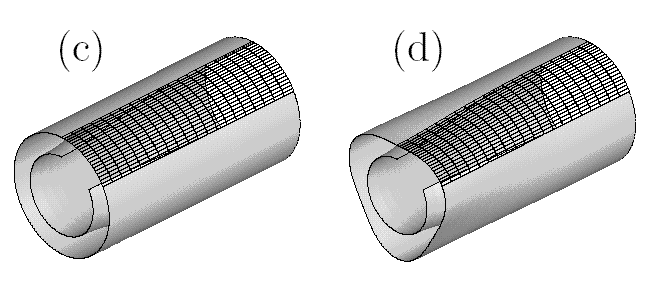
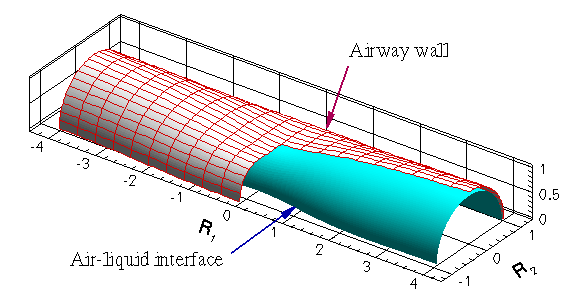
Figure 4:
The shape of the tube and the air-liquid interface during the growth
of primary axisymmetric axisymmetric (a-b) and secondary
non-axisymmetric (c-d) instability. A segment of the
air-liquid interface is not shown.
To reveal the
time-scales required for the transitions between the four stages shown in
Figs. 4(a-d), Fig. 5 illustrates the system's evolution by plotting
the radii of eight characteristic points (four on the air-liquid
interface; four on the tube wall).
At t=0, the air-liquid interface and the tube
wall are axisymmetric and we have R1=...=R4=1 and
Rh1=...=Rh4 = 0.9. During the initial stages of the Rayleigh
instability, the air-liquid
interface and the tube wall remain axisymmetric (Rh1 ~
Rh2 and Rh3 ~ Rh4) and the thickness of the
liquid lining increases/decreases at the two ends of
the domain: Rh1 and Rh2 grow while
Rh3 and Rh4
decrease. In its axisymmetric state, the airway wall is very stiff
and only deforms very little, R1 ~ ... ~ R4 ~
1. In agreement with the predictions from the linear stability
analysis, the tube wall begins to buckle at the compressed end
when t ~ 480, causing R3 to decrease and R4 to increase.
Buckling only occurs over a short axial length and the
opposite end of the domain remains approximately axisymmetric,
R1 ~ R2 ~ 1. Fig. 5
shows that the
final collapse occurs extremely rapidly -- the lines representing
the radii R3 and R4 become practically vertical. In this regime,
the adaptive time-stepping scheme used in the computations chooses
smaller and smaller time-steps to resolve the rapid collapse.
Ultimately, the convergence of the numerical scheme deteriorates
severely when roundoff errors begin to dominate the finite-difference
approximations in the time-stepping scheme. This prohibits the
continuation of the simulation beyond a certain degree of collapse.
However, at this stage in the simulation it is clear that the system
evolves rapidly towards a completely occluded configuration.
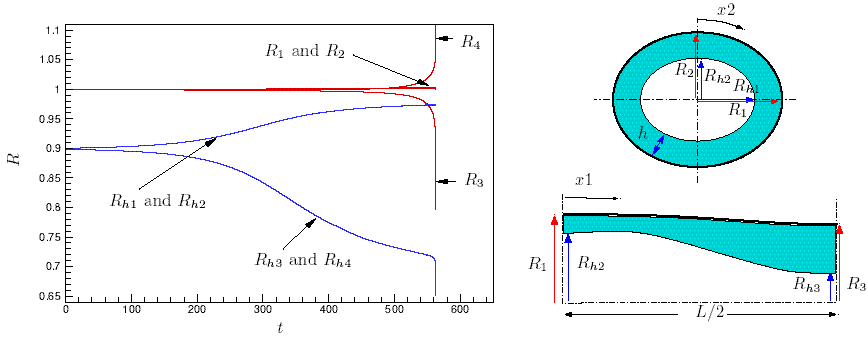
Figure 5:
The evolution of various radii on the tube wall and the
air-liquid interface (identified in the sketch on the right) as a
function of non-dimensional time. Note the rapid evolution during the
final stages of the collapse.
Again we performed a large number of such simulations to
investigate the effect of various parameters on the system's
behaviour. Most significantly, these parameter studies confirmed that
non-axisymmetric airway closure can occur for physiologically
realistic parameter values and that airway closure is possible even if the
volume of fluid in the liquid lining is insufficient
to occlude an axisymmetric airway.
Physiological implications
The main results of our mathematical/computational study are as follows
- Non-axisymmetric instabilities allow airway closure
to occur in cases where the volume of fluid in the liquid lining
is insufficient to occlude an axisymmetric airway.
- Non-axisymmetric instabilities can be initiated either
by an increase in the external (pleural) pressure or (more interestingly)
by the axisymmetric Rayleigh instability itself.
- The instabilities are predicted to occur for parameter values
which are physiologically realistic.
Obviously, the mathematical model used in our analysis represents
a strong simplification of the situation in vivo. We have deliberately
excluded many effects that we regard as secondary to the primary
instability mechanism. Neglected features include the presence of
airway bifurcations, the viscoelastic behaviour of the airway wall,
and the presence of parenchymal tethering.
We believe that inclusion of these effects would not change our
main results. For instance the length of an individual airway between two
successive bifurcations tends to be between 3-4 diameters.
This is long enough for the initial Rayleigh instability to develop.
Furthermore, our simulations predict airway collapse to occur
in a strongly localised fashion -- the non-axisymmetric collapse tends
to occur over a length of about two diameters. Hence, if the collapsing
region is located in the central part of an airway, the presence of
the bifurcations is unlikely to be of great importance.
Viscoelastic behaviour of the airway wall would affect the
time-scales for the instability but would not be able to suppress the
ultimate occlusion which is caused by the inability of the
elastic restoring forces to balance the compression generated by
surface tension.
Similarly, the presence of parenchymal tethering would stiffen the airway wall
and thus require larger compressive forces to achieve the same degree
of collapse. However, the surface-tension-driven compression
depends linearly on the curvature of the air-liquid interface which
increases rapidly with increasing collapse. Therefore, we expect
that even in the presence of tethering, surface tension forces
will ultimately be able to overcome the elastic restoring forces and
cause the airway to become occluded.
Acknowledgements/Funding
This project was funded by EPSRC grant GR/M75464/01.
Page last modified: December 10, 2002
Back to Matthias Heil's home page.