Introduction
Problems
of fluid transport through stochastic porous media arise in diverse applications
from medicine, the oil industry, air conditioning, fluid separation, battery
separator and sundry other contexts where permeable membranes are employed.
The most common
types of materials used in all of the above are nonwoven fabrics, ranging
from synthetic textiles and paper to thick glass fibre mats; all of these
are made by a fluid-laid stochastic process that deposits fibres into an evolving
pad as it develops structural rigidity. Here, the manufacturing process itself
is an evolving stochastic fluid flow as the pad grows by a stochastic filtering
mechanism. In other cases a complex transfer material may be a stochastically
porous plug or baffle region as an element in a deterministic flow system
and then we represent it by an appropriately coupled stack of porous strata.
We have a general
analytic model (cf References below) for the structural variability in such
stochastic porous media and we have an analytic solution for the statistical
features of transport of fluids through the media, under all types of flow
regimes: laminar, capillary, turbulent and molecular. We can accommodate also
the situation of progressive occlusion of pores by filtrate or the opposite
mechanism of back-washing.
The Stochastic
Flow Simulator (SFS) allows the deployment of our analytic results
to generate numerical values for spatial structural statistics and flow statistics,
which can then illustrate graphically the context and state of flow of any
chosen conditions of stochastic porous media and flow type.
In particular,
this software can be used to highlight the likelihood of extreme values in
evolving structure or to project end-usage flow behaviour under arbitrary
conditions.
Such monitoring
information in the form of graphics and animations can be absorbed at a glance
by the operator or process control engineer, for example when synthesized
from on-line data and refreshed in real time during manufacture or converting
operations. It can be used also in the design of new materials. We give below
some summaries of case studies and provide some illustrative animations.
SFS:
The Stochastic Flow Simulator
Functionality
The SFS
provides a representation of the spatial statistics of the pore size distribution
in a horizontal slice of an arbitrary stochastic porous medium. It does this
using computations in a large array of finite zones, to generate the local open
area distribution and then computes the local flow rate distribution, for arbitrary
flow modes---laminar, turbulent, capillary or molecular. These models allow
stacking of multilayer slabs of stochastic porous media of arbitrary porosity
and spatial variability.
Applicability
Such information
could be provided for on-line monitoring of the product quality in continuous
manufacturing processes for filter media of nonwoven or paper type. In applications
to flow processes, computations from our models can provide graphical animations
at any scale to assist operators in achieving rapid appreciation of the process
state and its evolution. So, control engineers could use raw on-line manufacturing
data to generate end-user behaviour and properties in arbitrary flow processes.
Quality Control
Off-line, in the
lab, SFS can use quality control data for a sample of the stochastic
medium to generate spatial statistics for the structure and for any desired
mechanism of fluid transport through it.
In practice,
the parameters for nonwoven filter fabrics can be derived from our analytic
procedures applied to optical or radiographic transmission images.
Geological
In the field, for
large-scale stochastic porous media, such as aggregate beds or sand-shale-rock
environments encountered in water and oil extraction, geophysical magnetometry
methods would be appropriate. Then SFS could allow estimation of flow
rates and variability.
Medical
At the other extreme,
the recovery of the human body from burns, trauma damage or surgery, involves
the growth of fibrin fibres in a more or less anisotropic rather haphazard array.
The evolving stochastic fibrous fibrin network is at the front line in defence
against infection and loss of body fluids, so its transport properties and their
evolution during healing need to be monitored and and SFS simulations
could allow projection of recovery patterns and the scheduling of continuing
treatment.
Demonstration
Distributions
in this set of small-scale demonstration graphics are set to unit mean and are
typical of the properties of stochastic porous filter-type barrier or separator
materials such as non-woven textiles, glass mats and paper. For such materials
the pore size distributions can be estimated by image analysis of radiographs
or micrographs, or from the statistics of mean flow rate growth with applied
pressure drop increase. Here are radiographs of two samples:

The animations
below show representative spatial distributions of the local pore radii and
local flow rate; other features can be represented similarly.
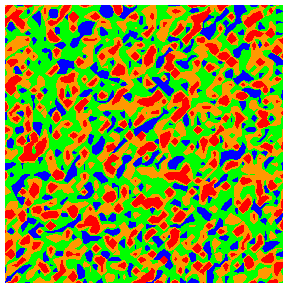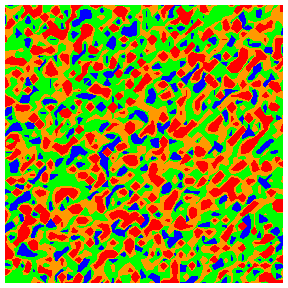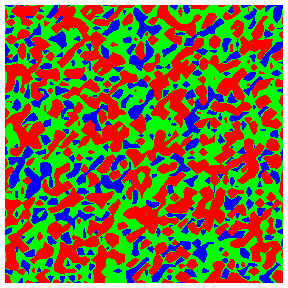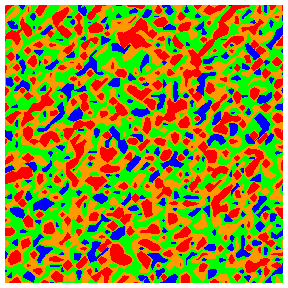
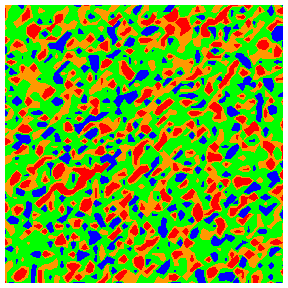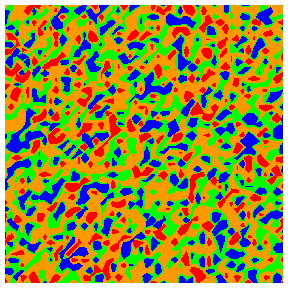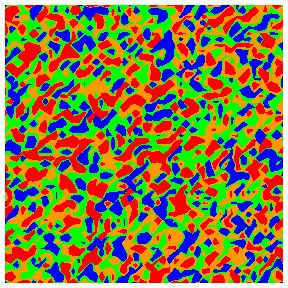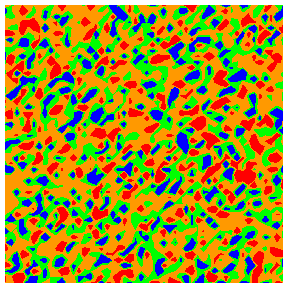
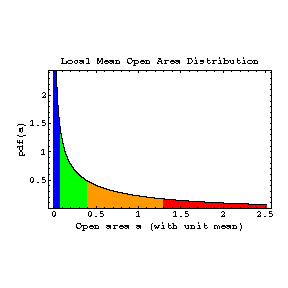
Colour codings for quartiles 1 to 4: blue, green, orange, red.
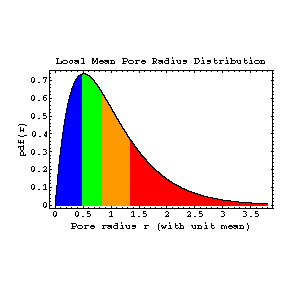 Local mean pore radii
Local mean pore radii 
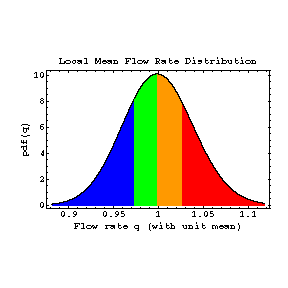 Local
mean flow rate
Local
mean flow rate 
Contact the authors for
more information:
References
-
Modeling a class of stochastic porous media.
C.T.J. Dodson and W.W. Sampson. App. Math. Lett. 10, 2 (1997) 87-89.
-
Spatial statistics of stochastic fibre networks.
C.T.J. Dodson and W.W. Sampson. J. Statist. Phys. 96, 1/2 (1999) 447-458.
-
Flow simulation in stochastic porous media.
C.T.J. Dodson and W.W. Sampson. Simulation, 74:6, (2000) 351-358.
-
Bivariate normal thickness-density structure in real near-planar stochastic
fibre networks.
C.T.J. Dodson and W.W. Sampson. J. Statist. Phys. 102, 1,2, (2001)
345-353.
-
On the distributions of mass, thickness and density of paper.
C.T.J. Dodson, Y. Oba and W.W. Sampson. Appita J. 54, 4 (2001) 385-389.
-
On the distribution of pore heights in layered random
fibre networks.
C.T.J. Dodson, Proc. 11th Fundamental Research Symposium,
Oxford, 17-21 September 2001, (2001) pp 1037-1042.

design:
chrisdod@blueyonder.co.uk


![]()
![]()


 Local mean pore radii
Local mean pore radii 

 Local
mean flow rate
Local
mean flow rate 
