
The University of Manchester The School of Mathematics Mathematics Service Teaching



Home Page Dropins/Office Hours Projects Videos
Articles Useful Links Gallery Astronomical Talks
1) A descriptive account of these minor planets e.g. their discovery, orbital characteristics etc.
2) A study of the Lagrangian points including a mathematical derivation of the location and stability of equilibria.
3) Some further work e.g. a) A computer simulation of the orbit of a sample Trojan asteroid. This will require the numerical solution of a system of two coupled second order Ordinary Differential Equations. b) A study of elliptic orbits in a rotating frame c) Modelling of the orbit of a specific asteroid in terms of its orbital elements.
References
1) "Exploration of the universe" G Abell, (useful for descriptive part and for basic explanation of laws of gravity)
2) "An introduction to Celestial Mechanics" Forest Ray Moulton
3) Numerical Recipes . W Press et al
This project can be taken in year 3 or year 4 as either a single-semester or full-year project. There are no specific pre-requisites for this project. Formerly titled "Jupiter and the Trojan Wars". Some videos supporting this project1) A more descriptive part on the types of Sundials
2) Studying and reporting on the means of designing sundials so that the lines do indeed correspond to the different hours of the day. This will involve a lot of work with trigonometry, matrices and projections.
3) Deriving the curve for the �equation of time� i.e. the difference between �sundial-time� and �clock-time� and, if time permits, seeing the effect on this quantity of changes in the Earth�s orbit.
References
�Sundials � their theory and construction� AE Waugh, Dover
M Muller �The equation of time�
This project can be taken in year 3 or year 4 as either a single-semester or full-year project. There are no specific pre-requisites for this project. Some videos supporting this projectAmong the advantages of computerised assessment is the ability to produce many variants of the same question stem so that students can enjoy repeated practice or so that different students can have different questions. Such variation is can be achieved by means of a parameter. For example, t (x + 4) can produce many different expansions each corresponding to a different value of t.
For some question stems, variants can be put together easily with all variants being of roughly the same degree of difficulty. In other cases, different variants can be different qualitatively. A question asking the user to solve the quadratic equation a x^2 + b x + c = 0 for parameters a, b and c will give different numbers of real roots depending on the parameters. Instead, the equation x^2 - (m + n) x + mn = 0 where parameters m+n and mn depend on more basic parameters m and n will always produce two real roots.
Intelligent algorithms involving parameters can increase the power of computerised assessment.
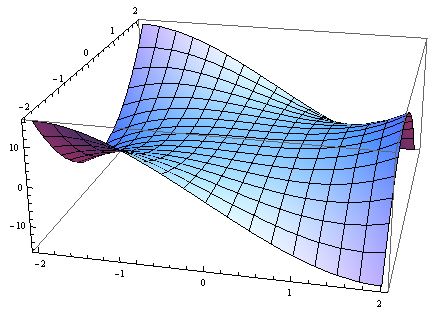
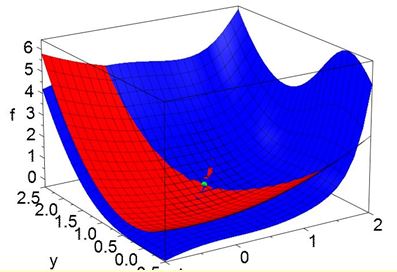
This project will explore algorithms for computerised assessment starting off with some simple cases and building up to more complicated scenarios e.g. multiple stationary values for a function of two variables. An understanding of mathematics through the core courses is a requirement for this project but the project can be carried out by students specialising in any area of mathematics. While no coding of algorithms is expected, it is anticipated that students will be able to use notation to record the algorithms used.
References
Computerised Assessment of Mathematics by C Sangwin, Oxford
Some videos supporting this projectThis project can currently be taken as a single-semester project in year 3