M4P33 Algebraic Geometry
2016-7, Term 2
Lecture notes (all lectures, including mastery material in Appendix A)
Problem sheets
Lecturer: Martin Orr
Assessment: Two courseworks (5% each), one exam (90%)
Coursework deadlines: 16 Feb, 14 Mar
What is algebraic geometry?
Algebraic geometry is the study of shapes defined as solutions to systems of polynomial equations in more than one variable. We call these shapes algebraic varieties. Examples include:
|
|

|
The circle 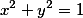 |
Cardioid 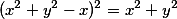 |
A quadric surface 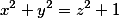 |
The types of questions we ask in algebraic geometry include:
- What is the dimension of an algebraic variety? Is it made of one component or many?
- Is the variety smooth or does it have singular points? If it is singular, can we find a related variety without singularities?
- What is the right way to count things? For example, we know that sometimes a root of a one-variable polynomial should be counted "more than once". How does this generalise to higher dimensions?
- Can we classify all algebraic varieties of a particular type?
- What if we have a family of algebraic varieties, defined by equations with parameters? How do the properties mentioned above vary as the parameters vary?
- Can we find algorithms to compute these properties starting from an explicit large system of polynomials?
Why study algebraic geometry?
The beauty of algebraic geometry lies in its combination of geometric ideas and algebraic tools. Algebra is used to give precise definitions and proofs of the foundations, in place of the analysis you may be used to from other kinds of geometry. A key benefit is that this allows us to use geometric ideas to study solutions of polynomials over any field, not just the real or complex numbers.
Areas of mathematics which use algebraic geometry include number theory, representation theory, coding and cyptography and string theory. It also has applications in mathematical biology, algebraic statistics and control theory, where interesting problems can be described in terms of the solutions to some system of polynomial equations and then studied using the methods of algebraic geometry.
What will be in this course?
In this course, we will aim to focus on geometric intuition and examples. We will make use of commutative algebra, especially calculations with polynomials, but aim to avoid more advanced or technical concepts from algebra.
We will see the interplay between algebra and geometry in the foundations of the subject, for example the Nullstellensatz and basic properties of dimension. The core concepts will be illustrated with many interesting examples. We will not just give formal definitions of properties such as dimension and smoothness, but also see ways of calculating these for concrete examples.
By the end of this course:
-
You will be able to define affine and projective varieties, morphisms and rational maps between them, the Zariski topology, irreducible components of a variety and the concepts of dimension and smoothness for algebraic varieties.
-
You will understand a proof of the Nullstellensatz and how this allows us to translate between affine varieties and commutative algebra.
-
You will be able to prove Chevalley's theorem on the image of a morphism of algebraic varieties, the semicontinuity theorem for dimension and (if time permits) Bertini's theorem on the smoothness of hyperplane sections.
-
You will be able to apply this knowledge to examples such as the twisted cubic, quadrics, the Segre embedding, Grassmannians and Fano varieties.
-
You will know an outline of the proof of the beautiful classical theorem that there are 27 lines on a cubic surface.

|
| A cubic surface with the 27 lines on it |
How does this course relate to other courses?
-
M3P8 Algebra 3 - Concepts from Algebra 3 such as rings, ideals and Noetherian rings are essential for the Algebraic Geometry course.
-
M4P55 Commutative Algebra - The Algebraic Geometry course will use some ideas from Commutative Algebra such as prime and maximal ideals, transcendental and algebraic field extensions and Hilbert's basis theorem. In the other direction, algebraic geometry provides a useful new way of thinking geometrically about commutative algebra.
Therefore students taking Algebraic Geometry are recommended to also take Commutative Algebra. However we will try to avoid the use of more sophisticated concepts from commutative algebra. When we use theorems from commutative algebra, it will either be possible to treat them as black boxes without knowing the proofs, or we will give a proof where this has geometric significance. Hence Commutative Algebra is not absolutely essential as a pre-requisite.
-
M4P63 Algebra 4 - The contents of Algebra 4 are not directly relevant to this Algebraic Geometry course, although they will be extremely useful for students who go on to study algebraic geometry further.
-
M3P20 Geometry I: Algebraic Curves - Algebraic curves are the simplest algebraic varieties, and hence the algebraic curves course provides good background for Algebraic Geometry. The Algebraic Geometry course will not assume any prior knowledge of algebraic curves. The Algebraic Geometry course will take a more sophisticated approach, working with higher-dimensional varieties throughout, so direct duplication between the two courses should be small.
What books are useful for this course?
-
Reid, Undergraduate Algebraic Geometry - This is a nice short book at the right level. It covers most of the key concepts of this course but not all of the applications and examples we will look at.
-
Shafarevich, Basic Algebraic Geometry 1 - Chapter 1 and section 2.1 of this book form a good textbook for this course (if time permits we will cover a bit more of chapter 2). It is written more densely than Reid, but its proofs are often closer to the approaches we will use in this course. The book goes on to cover much more material - this would be a good book to look at if you want to read more of the theory of algebraic geometry.
-
Smith et al., An Invitation to Algebraic Geometry - This is another highly recommended book. It focusses more on examples and motivation and less on technicalities than Reid's book, omitting many proofs.
-
Harris, Algebraic Geometry: A First Course - This is a very nice book containing many examples of algebraic varieties, including those which we will cover in the course. It uses an approach which is primarily geometric and omits heavier algebra, similar to the spirit of the course. There is far more material in this book than we will cover in the course, and it is presented quite densely.
Attributions for figures
The figures of the circle and cardioid were created by Martin Orr using gnuplot. These figures are in the public domain.
The figure of a quadric surface is a cropped version of a figure created by Sam Derbyshire and obtained from Wikimedia Commons. It is used under the CC BY-SA 4.0 license.
The figure of a cubic surface with 27 lines was created by O. Labs and D. van Straten and obtained from the Cubic Surfaces Homepage at the University of Mainz.