Tropical mathematics is mathematics over the tropical semiring; that is, the set of real numbers (sometimes augmented with the extra element minus infinity) under the operations of addition and maximum. A good overview of tropical mathematics can be found here. Matrices over the tropical semiring arise naturally in many application areas, such as combinatorial optimisation and scheduling and phylogenetics.
In 2012 and 2013 I gave a graduate level course on some basic aspects of tropical linear algebra.
From 2010-2012 I held a research position at the University of Manchester, working with Dr Mark Kambites on the EPSRC funded research project `Multiplicative Structure of Tropical Matrix Algebra'. Other members of our research group include/have included Zur Izhakian and Christopher Hollings.
The aim of the project was to understand the algebraic structure of such matrices under multiplication. It turns out that many natural questions about this algebraic structure can be answered using the language of the geometry of tropical convex sets and polytopes. For example, some of our research has shown that the von Neumann regular matrices are exactly those with row space a polytope of pure dimension equal to the row and column rank of the matrix. It follows from this that almost all of the numerous notions of rank which have been studied for tropical matrices coincide in the case of regular matrices.
A simple (but key) observation is that there is connection between the tropical convex sets generated by the rows (respectively columns) and Green’s L-relation (respectively R-relation). The project has resulted in a complete description of the remaining relations (H, D and J). Moreover, we described the relationship between Green's J -relation and various ideas of the `rank' of a tropical matrix. We have also studied the notion of projectivity for tropical semimodules and the related concepts of idempotent and von Neumann regular matrices. For more details, have a look at my publications.
In 2008 I was part of a large interdisciplinary research team, called CICADA, working at the boundaries between mathematics, computer science and control engineering. In particular, I studied algebraic structures related to asynchronous systems, such as the max-plus (or tropical) semiring. I organised a weekly reading group on tropical mathematics, which included guest seminars from leading max-plus specialists.
In joint work with Dr Mark Kambites we described the multiplicative structure of the semiring of 2 x 2 tropical matrices. In joint work with Professor Dave Broomhead and Professor Steve Furber I showed that a `heuristic' used to calculate the micromum clock period in the early design of the ARM hardware corresponds exactly to the solution of a tropical eigenvalue problem.
In my PhD thesis I considered the problem of describing the module structure of the free Lie algebra under the action of a group. In my first year as a PhD student I gave a combinatorial proof of a Klyachko's theorem on Lie representations of the general linear group in characteristic zero (see below).
As part of my thesis I also calculated some specific module decompositions of Lie powers in characteristics two and three. This led to joint work with Professor Roger Bryant in which we gave a description, up to isomorphism, of certain modules occurring in the Decomposition Theorem of Bryant and Schocker. As an application of the decompositions obtained in my thesis, in joint work with Professor Stohr we proved that certain free centre-by-nilpotent-by-abelian groups are torsion-free.
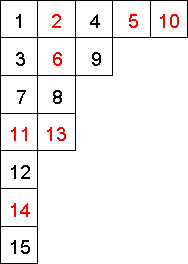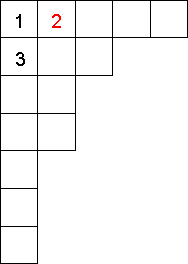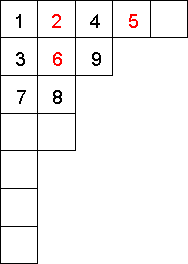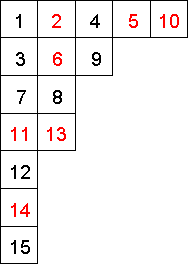Let λ be a partition of a positive integer n. A Young diagram of shape λ is a collection of n boxes arranged in left justified rows, whose lengths correspond to parts of λ.
A standard tableau of shape λ is a numbering of the corresponding Young diagram with the numbers from 1 to n, in such a way that the entries increase along each row and down each column.
We say that an entry i in a standard tableau is a descent if the entry i+1 occurs in any row below the row containing i. The sum of all descents in a standard tableau T is called the major index of T.
For example, the image to the right illustrates the creation of a standard tableau of shape (5,3,22,13). Here the descents are shown in red.
In my first year as a PhD student I proved the following theorem:
Theorem
Let n≥3 and let λ be a partition of n. There exists a standard tableau of shape λ with major index coprime to n if and only if λ ≠ (1n), (n), (22) or (23).
To find out what this has to do with the module structure of free Lie algebras, have a look at the following poster.
In 2010 I had a research position working with Dr Karin Erdmann at the University of Oxford on the EPSRC funded research project `Modular Lie powers and applications'. In joint work with Professor Roger Bryant, I considered a modular version of a result of Klyachko on Lie powers of the natural module for GL(n,K). Our methods, which relied upon some earlier joint work, gave results about the kind of indecomposable tilting modules occurring in the Lie power.
Unfortunately our methods did not work well for degrees pm or 2pm. For GL(2,K) these cases were analysed in some detail in a further paper with Dr Karin Erdmann.
As an application of the decompositions obtained in my thesis, in joint work with Professor Ralph Stohr we proved that certain free centre-by-nilpotent-by-abelian groups are torsion-free. In further joint work we proved a result on torsion in free central extensions using techniques developed for modular Lie powers of relation modules.
In 2009 I had a research position working with Professor Roger Bryant at the University of Manchester on the EPSRC funded research project `Modular Lie powers and applications'. Part of my work involved using computer algebra packages such as GAP and MAGMA to obtain experimental evidence of certain decompositions of Lie powers of modules for cyclic p-groups in characteristic p.
We also studied the Adams operations on the Green ring of a finite group. We proved several periodicity results, giving the precise period in the case of a cyclic p-group.