Week 1 Introduction. How to detect and correct errors?
Version 2023-09-30. To PDF of this week only Open the whole set of notes in PDF
These notes are being revised to reflect the content of the course as taught in the 2023/24 academic year. Questions and comments on these lecture notes should be directed to Yuri.Bazlov@manchester.ac.uk.
Synopsis
We discuss information transmission and introduce the most basic notions of Coding Theory: channel, alphabet, symbol, word, Hamming distance and of course code. We show how a code can detect and correct some errors that occur during transmission. We illustrate the process using two simple examples of codes.
What is information?
It is fair to say that our age is the age of information. Huge quantities of information and data literally flow around us and are stored in various forms.
Information processing gives rise to many mathematical questions. Information needs to be processed because we may need, for example, to:
-
• store the information;
-
• encrypt the information;
-
• transmit the information.
For practical purposes, information needs to be stored efficiently, which leads to problems such as compacting or compressing the information. For the purposes of data protection and security, information may need to be encrypted. We will NOT consider these problems here. The course basically addresses one (extremely important) problem that arises in connection with information transmission.
We do not attempt to give an exhaustive definition of information. Whereas some mathematical models for space, time, motion were developed hundreds of years ago, the modern mathematical theory of information was only born in 1948 in the paper A Mathematical Theory of Communication by Claude Shannon (1916–2001). The following will be enough for our purposes:
Definition: information, alphabet, symbol
Fix a finite set \(F\) of two or more elements and call it the alphabet.
Elements of \(F\) are called symbols.
By information we mean a stream (a sequence) of symbols.
What does it mean to transmit information? What is a channel?
Informally, it means that symbols are sent by one party (the sender) and are received by another party (receiver). The symbols are transmitted via some medium, which we will in general refer to as the channel. More precisely, the channel is a mathematical abstraction of various real-life media such as a telephone line, a satellite communication link, a voice (in a face to face conversation between individuals), a CD (the sender writes information into it — the user reads the information from it), etc.
In this course we will assume that when a symbol is fed into the channel (the input symbol), the same or another symbol is read from the other end of the channel (the output symbol). Thus, we will only consider channels where neither erasures (when the output symbol is unreadable) nor deletions (when some symbols fed into the channel simply disappear) occur. Working with those more general channels requires more advanced mathematical apparatus which is beyond this course.
Importantly, we assume that there is noise in the channel, which means that the symbols are randomly changed by the channel. Our model of information transmission is thus as follows:
\[ \fbox {sender} \xrightarrow {\text {stream of symbols}} \fbox {channel} \xrightarrow [\text {with random changes}]{\text {stream of symbols}} \fbox {receiver} \]
The above discussion leads us to the following simplified definition of a channel, which will be sufficient for this course.
Definition: memoryless channel
Fix the alphabet \(F.\) A memoryless channel is a function which has one argument — the input symbol \(x\in F\) — and one output, a random output symbol \(y\in F\) which depends only on \(x.\)
The definition says for each \(x\in F\) which is sent via the channel (i.e., given as input), there is a probability distribution on \(F\) which shows which symbol will be received (output) with which probability.
A noiseless channel is the identity function which reads the input symbol \(x\) and outputs \(x\) with probability \(1.\) However, more generally a channel is noisy, meaning that, if \(x\) is sent, the received symbol can be either \(x\) with probability less than \(1,\) or another symbol.
Memoryless means that the received symbol depends only on \(x\) and not on symbols which may have been sent via the channel before \(x.\) We describe an example of a memoryless noisy channel, \(\mathit {BSC}(p),\) below.
When a symbol \(x\in F\) is sent, there are two possible outcomes:
-
• The received symbol is \(x.\) We say that no error occurred in this symbol.
-
• The received symbol is \(y\ne x.\) An error occurred in this symbol.
We formalise this in
Definition: symbol error
A symbol error is an event where a symbol \(x\in F\) is sent via the channel, and the received symbol is \(y\) such that \(y\ne x.\)
The binary symmetric channel with bit error rate \(p\)
Our most basic example of a channel “speaks” the binary alphabet, which we will now define.
Definition: binary alphabet, bit
The binary alphabet is the set \(\F _2=\{0,1\}.\)
A bit (the same as binary symbol) is an element of \(\F _2.\)
Definition: \(\mathit {BSC}(p)\)
Theoretically, we can consider \(\mathit {BSC}(p)\) with \(0\le p<\frac 12.\) Real-world binary channels are modelled by \(\mathit {BSC}(p)\) with small \(p\) ranging from \(10^{-2}\) (modem over a bad copper telephone line in 1950s) down to \(10^{-13}\) (modern fibre optics).
There are other channels which are mathematical models of media not well-approximated by \(\mathit {BSC}(p).\) This includes channels which “speak” alphabets other than \(\F _2.\) Much of theory we develop will work for general channels. However, explicit caculation of probabilities will only be done for \(\mathit {BSC}(p).\)
What is a code and what is it used for?
A word is a finite sequence of symbols, and a code is a set of words. However, in this course we only consider block codes — this means that all the words in the code are of the same length \(n.\) Although variable length codes are used in modern applications, they are beyond the scope of the course, and so we refer to block codes simply as codes.
The main application of codes is channel coding. This means that the sender uses the chosen code to encode information before sending it via the channel. This allows the receiver to achieve one of the following goals:
-
• detect most errors that occur in the channel and ask the sender to retransmit the parts where errors are detected; or
-
• correct most errors that occur in the channel (nothing is retransmitted).
We will now formalise the definition of a code, explain encoding, and then show how error detection works and how error correction works.
Definition: word
A word of length \(n\) in the alphabet \(F\) is an element of \(F^n.\) Here \(F^n\) is the set of all \(n\)-tuples of symbols:
\[ F^n=\{\ul v=(v_1,v_2,\ldots ,v_n)\mid v_i\in F,\ 1\le i \le n\}. \]
Notation: words
We may write a word \((w_1,w_2,\dots ,w_n)\in F^n\) as \(w_1w_2\dots w_n\) if this is unambiguous. So, for example, the binary words \(000,\) \(101\) and \(111\) belong to \(\F _2^3,\) and are more fully written as \((0,0,0),\) \((1, 0,1)\) and \((1,1,1),\) respectively.
We will denote words by underlined letters: \(\ul w.\) Thus, \(\ul w = w_1 w_2 \dots w_n\) where \(w_i\) denotes the \(i\)th symbol of the word \(\ul w.\)
Definition: code, codeword
A code of length \(n\) in the alphabet \(F\) is a non-empty subset of \(F^n.\) We will denote a code by \(C.\) That is, \(C\subseteq F^n,\) \(C\ne \varnothing .\)
A codeword is an element of the code.
The sender and the receiver choose a code \(C\subseteq F^n\) for channel coding. To perform error detection and correction, the sender must send only codewords via the channel. However, information may contain arbitrary sequences of symbols, not just codewords, and so needs to be encoded.
The encoding procedure that we consider requires the code \(C\) to have the same number of elements as \(F^k,\) the set of words of length \(k,\) for some positive integers \(k.\) Note that \(C\subseteq F^n\) and \(\#C=\#(F^k)\) means that \(k\le n.\)
Definition: encoder
An encoder for a code \(C\) is a bijective function \(\Encode \colon F^k \to C.\)
Here is what the sender must do.
Procedure: encoding
Before transmission, a code \(C\) and an encoder \(\Encode \colon F^k \to C\) must be fixed.
-
• The information stream is split up into chunks of length \(k,\) called messages.
-
• The sender takes each message \(\ul u\in F^k\) and replaces it with the codeword \(\ul c = \Encode (\ul u).\)
-
• Each codeword \(\ul c\) is sent into the channel.
Note: “\(\ul c\) sent into the channel” means that the symbols \(c_1,c_2,\dots ,c_n\) are consecutively sent via the channel.
How to use a code to detect errors?
Recall that the sender transmits only codewords:
\[ \fbox {sender} \xrightarrow [\ul c\in C]{\text { codeword }} \fbox {channel} \xrightarrow [\ul y\in F^n]{\text { received word }} \fbox {receiver} \]
The sender transmits a codeword \(\ul c\in C.\) The receiver receives a word \(\ul y=y_1y_2\dots y_n\) which may not be not the same as \(\ul c,\) due to noise in the channel. Of course, if \(\ul y\notin C,\) the receiver knows that \(\ul y\) is not what was sent.
If, however, \(\ul y\in C,\) the receiver has no way of knowing whether an error occurred, and must assume that there was no error. The above suggests the following
Procedure: error detection
-
1. The sender sends a codeword \(\ul c \in C\) via the channel.
-
2. The receiver receives a word \(\ul y\in F^n:\)
-
• if \(\ul y\notin C,\) this is a detected error, and the receiver asks the sender to retransmit the current codeword;
-
• if \(\ul y\in C,\) the receiver accepts \(\ul y.\) If \(\ul y\in C\) and \(\ul y\ne \ul c,\) this is an undetected error.
-
-
3. If there are any more codewords to transmit, return to step 1.
We assume that every detected error is eliminated by retransmitting the codeword one or more times. These retransmissions slow down the communication, but eventually the information accepted by the receiver will consist of correct codewords and codewords containing an undetected error.
How good is a code at detecting errors?
To select the most suitable error-detecting code for a particular application, or to decide whether to use a code at all, we need to measure how good is error detection.
One way to quantify this is to ask how many symbol errors must occur in a codeword to result in an undetected error. We will investigate this next week. This approach does not explicitly take the parameters of the channel into account.
Another approach is to calculate \(P_{\mathrm {undetect}}(C)\) for a particular channel:
Definition: \(P_{\mathrm {undetect}}(C),\) the probability of an undetected error
Suppose that an alphabet \(F\) and a channel are given. Let \(C\subseteq F^n\) be a code. Assume that a random codeword from \(C\) is sent via the channel. Then \(P_{\mathrm {undetect}}(C)\) is the probability that an undetected error occurs in the received word.
Note that \(P_{\mathrm {undetect}}(C)\) expresses the average proportion of wrong codewords accepted by the receiver. Good error detection means that \(P_{\mathrm {undetect}}(C)\) is low.
\(E_3:\) an example of a code used for error detection
We now introduce the code \(E_3.\) Later, it will be seen as a particular case of \(E_n,\) the binary even weight code of length \(n.\) The code consists of four codewords:
Definition: the code \(E_3\)
\(E_3=\{000,011,101,110\},\) a subset of \(\F _2^3.\)
To set up error detection based on \(E_3,\) we need an encoder. A standard choice is as follows: \(E_3\) consists exactly of the binary words of length \(3\) which have an even number of \(1\)s. Hence a \(2\)-bit message can be encoded into a \(3\)-bit codeword of \(E_3\) by appending \(0\) or \(1\) so as to make the total number of \(1\)s even. The appended bit is known as the parity check bit:
Example: encoder for \(E_3\) (appending the parity check bit)
Define \(\Encode \colon \F _2^2 \to E_3\) by \(00 \mapsto 000,\) \(01\mapsto 011,\) \(10\mapsto 101,\) \(11\mapsto 110.\)
Thus, if the information which needs to be transmitted is \(001011,\) it is broken up into messages \(00,\) \(10,\) \(11,\) then \(E_3\)-encoded as codewords \(000,\) \(101,\) \(110\) and sent via the channel.
How good is \(E_3\) at detecting errors? \(E_3\) is a binary code, so we may assume that the communication channel is \(\mathit {BSC}(p)\) and calculate \(P_{\mathrm {undetect}}(E_3).\)
Suppose that the codeword \(000\in E_3\) is sent. For each word \(\ul y\in \F _2^3\) we find the probability that \(\ul y\) is received:
-
• \(000\) is received with probability \((1-p)^3\) — for each of the three bits, the probability of arriving unchanged is \(1-p;\)
-
• \(001,\) \(010,\) \(100\) have probability \(p(1-p)^2\) each, and are detected errors;
-
• \(011,\) \(101\) and \(110,\) with probability \(p^2(1-p)\) each, are undetected errors;
-
• \(111\) has probability \(p^3\) to be received, and is a detected error.
The total probability of an undetected error is \(3p^2(1-p).\)
If any codeword other than \(000\) is sent, the probability of an undetected error is the same (Exercise: check this).
Hence \(P_{\mathrm {undetect}}(E_3)=3p^2(1-p),\) assuming the channel is \(\mathit {BSC}(p).\) Later in the course, we will obtain a formula for \(P_{\mathrm {undetect}}(C)\) for a large class of binary codes \(C\) to avoid doing a case-by-case analysis each time.
Thus, if information is sent unencoded (\(E_3\) is not used, no error detection), the average proportion of incorrect bits in the output will be \(p.\) If, however, \(E_3\) is used for error detection, the average proportion of incorrect bits in the output will be less than \(3p^2.\) If \(p\ll 1,\) then \(3p^2\) is much less than \(p\) — communication becomes more reliable when an error-detecting code is used.
How to use a code for error correction?
In order to take full advantage of error detection, the receiver should be able to contact the sender to request retransmission. In some situations this is not possible. We will now see how to modify the above error detection set-up so that the receiver could recover from errors, without contacting the sender.
Mathematics behind error correction got to be associated with the name of Richard Hamming (1915–1998) who came up with an idea to set up an efficient error-correcting code. In engineering literature, the set-up we are going to describe is referred to as forward error correction (FEC).
The first basic concept we need for error correction is distance between words.
Definition: Hamming distance
The Hamming distance between two words \(\ul x,\ul y\in F^n\) is the number of positions where the symbol in \(\ul x\) differs from the symbol in \(\ul y:\)
\[ d(\ul x, \ul y) = \#\{i\in \{1,\ldots ,n\} : x_i\ne y_i\}. \]
Example: Hamming distace between some pairs of binary words
For example, in the set \(\F _2^3\) of \(3\)-bit binary words one has
\[d(101,111)=1 \qquad \text {and} \qquad d(101,000)=2. \]
Of course,
\[ d(101,101)=0. \]
Lemma 1.1: properties of the Hamming distance
For any words \(\ul x, \ul y, \ul z\in F^n,\)
-
1. \(d(\ul x,\ul y)\ge 0;\) \(d(\ul x,\ul y)= 0\) iff \(\ul x = \ul y.\)
-
2. \(d(\ul x,\ul y)=d(\ul y,\ul x).\)
-
3. \(d(\ul x,\ul z)\le d(\ul x,\ul y)+d(\ul y,\ul z)\) (the triangle inequality).
Remark: recall that a function \(d(-,-)\) of two arguments which satisfies axioms 1.–3. is called a metric. This is familiar to those who studied Metric spaces. The Lemma says that the Hamming distance turns \(F^n\) into a metric space.
-
Proof. 1. Since \(d(\ul x,\ul y)\) is a cardinality of a subset of \(\{1,\dots ,n\},\) it is an integer between \(0\) and \(n.\) Moreover, \(d(\ul x,\ul y)\) is \(0\) iff \(x_i=y_i\) for all \(i\) meaning that \(\ul x=\ul y.\)
2. Symmetry is clear as \(x_i\ne y_i\) is equivalent to \(y_i\ne x_i.\)
3. An index \(i\) such that \(x_i=y_i\) and \(y_i=z_i\) does not contribute to \(d(\ul x,\ul y)\) nor to \(d(\ul y,\ul z)\) nor to \(d(\ul x,\ul z)\) (because \(x_i=z_i).\)
An index \(i\) such that \(x_i\ne y_i\) or \(y_i\ne z_i\) contributes at least \(1\) to \(d(\ul x,\ul y)+d(\ul y,\ul z),\) and can contribute at most \(1\) to \(d(\ul x,\ul z).\)
Thus, every index \(i\) contributes to left-hand side at most as much as to the right-hand side. Summing for \(i\) running over \(\{1,\dots , n\}\) proves the triangle inequality. □
We will now use the Hamming distance to set up error correction. Let \(C\subseteq F^n\) be a code.
Definition: decoder, nearest neighbour
A decoder for \(C\) is a function \(\Decode \colon F^n\to C\) such that for any \(\ul y\in F^n,\) \(\Decode (\ul y)\) is a nearest neighbour of \(\ul y\) in \(C.\)
A nearest neighbour of \(\ul y\in F^n\) in \(C\) is a codeword \(\ul c\in C\) such that
\[ d(\ul c,\ul y) = \min \{d(\ul z,\ul y): \ul z\in C\}. \]
In order to use error correction, the sender and the receiver choose a decoder \(\Decode \colon F^n\to C.\) The sender transmits codewords of \(C.\) The receiver decodes the received words:
\[ \fbox {sender} \xrightarrow [\ul c\in C]{\text { codeword }} \fbox {channel} \xrightarrow [\ul y\in F^n]{\text { received word }} \xrightarrow [\ \Decode (\ul y)\in C\ ]{\text { decoded word }} \fbox {receiver} \]
Remark: what the decoder does; unencode
Thus, if the received word \(\ul y\) is not a codeword, the decoder assumes that the codeword closest to \(\ul y\) was sent, and outputs such a codeword.
To restore the original message \(\ul u\in F^k,\) the codeword \(\ul c\in C\) can be unencoded: \(\ul u = \Encode ^{-1}(\ul c).\)
It may happen that some words \(\ul y\in F^n\) have more than one nearest neighbour in \(C,\) which means that there exist more than one decoder function. In this course we assume that the receiver fixes one particular decoder to make decoding deterministic.
Definition: decoded correctly
In the above setup, let \(\ul c\in C\) be the transmitted codeword and let \(\ul y\in F^n\) be the received word. If \(\Decode (\ul y)=\ul c,\) we say that the received word is decoded correctly.
The following Claim shows that the error-correcting setup makes sense — at least, if no symbol errors occurred in a codeword, the decoder will not introduce errors! Strictly speaking, the Claim is unnecessary, because it will follow from part 2 of Theorem 2.1 given later.
Claim: a codeword is always decoded to itself
A codeword is its own unique nearest neighbour: indeed, \(d(-,-)\) is non-negative hence \(d(\ul c,\ul c)=0=\min \{d(\ul z,\ul c): \ul z\in C\}.\)
Therefore, a codeword is always decoded to itself:
\[ \ul y\in C\quad \implies \quad \Decode (\ul y)=\ul y. \]
How good is a code at correcting errors?
This can be measured in two ways. First, one can determine the maximum number of symbol errors that can occur in a codeword which the decoder is guaranteed to correct. Second, one can calculate the probability \(P_{\mathrm {corr}}(C)\) of correct decoding for a specific channel. We will return to these later.
\(\Rep (3,\F _2):\) an example of a code used for error correction
It is easy to see that the code \(E_3\) is not suitable for error correction. Indeed, suppose the received word was \(100.\) We note that \(100\) has three nearest neighbours in \(E_3,\) namely \(000,\) \(110\) and \(101,\) all at distance \(1.\) There is no reasonable way to decide which of these was sent, so no efficient decoder.
We define a new code, the binary repetition code of length \(3.\)
Definition: the code \(\Rep (3,\F _2),\) encoder
\(\Rep (3,\F _2) = \{000,111\},\) a subset of \(\F _2^3.\)
Define \(\Encode \colon \{0,1\}\to \Rep (3,\F _2)\) by \(\Encode (0)=000,\) \(\Encode (1)=111.\)
One can observe that every word in \(\F _2^3\) has exactly one nearest neighbour in the code \(\Rep (3,\F _2),\) and here is how the decoder works: for each word \(\ul y\in \F _2^3,\) the arrow points from \(\ul y\) to \(\Decode (\ul y)\in \Rep (3,\F _2).\)
Example: the decoder for \(\Rep (3,\F _2)\)
Why develop any more theory and not just use \(E_3\) and \(\Rep (3,\F _2)\)?
The problem with these codes is that, for every bit of information, you need to transmit \(1.5\) bits (using \(E_3)\) or \(3\) bits (using \(\Rep (3,\F _2)),\) because encoding increases the number of bits. Such an increase in transmission costs may be unacceptable, and so more efficient codes need to be designed.
Concluding remarks for Chapter 1
Codes have been used for error correction for thousands of years: a natural language is essentially a code! If we “receive” a corrupted English word such as PHEOEEM, we will assume that is has most likely been THEOREM, because this would involve fewest mistakes.
The following examples are part of historical background to Coding Theory and are not covered in lectures.
Example 1 (a real-world use of Coding Theory in scientific research)
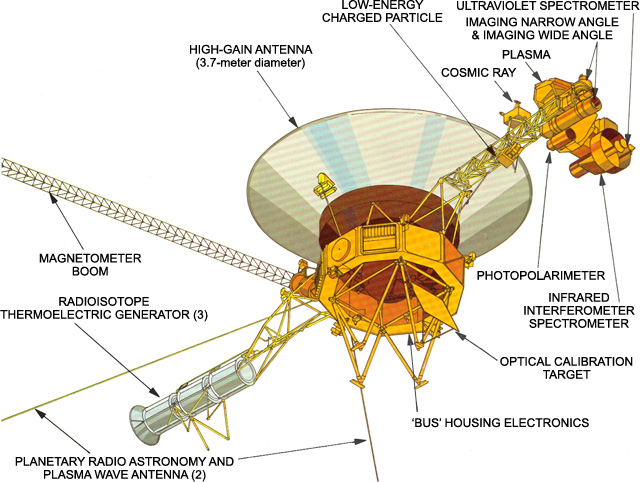
Figure 1.1: The Voyager spacecraft. Image taken from https://voyager.jpl.nasa.gov/mission/spacecraft/instruments/
Voyager 1 is a spacecraft launched by NASA in 1977. Its primary mission was to explore Jupiter, Saturn, Uranus and Neptune. Lots of precious photographs and data was sent back to Earth. Later, NASA scientists claimed that Voyager 1 reached the interstellar space.
Messages from Voyager 1 travel through the vast expanses of interplanetary space. Given that the spacecraft is equipped with a mere 23 Watt radio transmitter (powered by a plutonium-238 nuclear battery), it is inevitable that noise, such as cosmic rays, interferes with its transmissions. In order to protect the data from distortion, it is encoded with the error-correcting code called extended binary Golay code. We will look at this code later in the course. Newer space missions employ more efficient and more sophisticated codes.
Example 2 (CD, a compact disc)
A more down-to-earth example of the use of error-correcting codes. A CD can hold up to 80 minutes of music, represented by an array of zeros and ones. The data on the CD is encoded using a Reed-Solomon code. This way, even if a small scratch, a particle of dust or a fingerprint happens to be on the surface of the CD, it will still play perfectly well — all due to error correction.
However, every method has its limits, and larger scratches or stains may lead to something like a thunderclap during playback!
Example 3 (one of the first uses of a code for error correction)
In 1948, Richard Hamming was working at the famous Bell Laboratories. Back then, the data for “computers” was stored on punch cards:
Figure 1.2: A punch card. Image from http://www.columbia.edu/cu/computinghistory
pieces of thick paper where holes represented ones and absences of holes represented zeros. Punchers who had to perforate punch cards sometimes made mistakes, which frustrated Hamming.
Hamming was able to come up with a code with the following properties: each codeword is 7 bits long, and if one error is made in a codeword (i.e., one bit is changed from 0 to 1 or vice versa), one can still recover the original codeword. This made the punch card technology more robust, as a punch card with a few mistakes would still be usable. The trade-off, however, was that the length of data was increased by 75%: there are only 16 different codewords, therefore, they can be used to convey messages which have the length of 4 bits.
The original Hamming code will be introduced in the course soon!