Contents

Random numbers

% uniform [0, 1]
v = rand(1,1000000);
mean(v)
std(v)

% standard normal
v = randn(1,1000000);
mean(v)
std(v)

ans =
   0.500465275048761
ans =
   0.288946124163335
ans =
    -9.716953244899469e-04
ans =
   0.999581390315130

Monte Carlo to estimate pi

N = 1000000;
v = 2*rand(2,N)-1;
sum(v(1,:).^2+v(2,:).^2<1)/N*4

ans =
   3.140796000000000

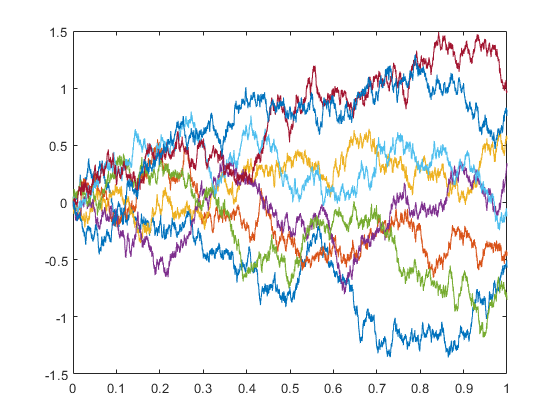
Generate Brownian motion

M = 8;
dt = 0.0001;
T = 0:dt:1;
V = randn(M,length(T))*sqrt(dt);
S = cumsum(V,2);

for k = 1:M
    plot(T,S(k,:));
    hold on
end
hold on

Solve the forced harmonic oscillator symbolically

w'' + 2k/(rho*L)*w = -p0/rho*cos(omega*t)

syms w(t) k rho L p0 omega
ode = diff(w(t),t,t) + 2*k/(rho*L)*w(t) == -p0/rho*cos(omega*t)
Dw = diff(w);
cond = [ w(0)==0, Dw(0)==0] % subs(diff(w(t),t),t,0)=0
dsolve(ode,cond)

ode =
diff(w(t), t, t) + (2*k*w(t))/(L*rho) == -(p0*cos(omega*t))/rho
cond =
[w(0) == 0, subs(diff(w(t), t), t, 0) == 0]
ans =
(L*p0*exp((2^(1/2)*t*(-L*k*rho)^(1/2))/(L*rho)))/(2*(- L*rho*omega^2 + 2*k)) + (L*p0*exp(-(2^(1/2)*t*(-L*k*rho)^(1/2))/(L*rho)))/(2*(- L*rho*omega^2 + 2*k)) + (2^(1/2)*L^(1/2)*p0*exp(-(2^(1/2)*k^(1/2)*t*1i)/(L^(1/2)*rho^(1/2)))*exp((2^(1/2)*t*(-L*k*rho)^(1/2))/(L*rho))*(omega*sin(omega*t) - (2^(1/2)*k^(1/2)*cos(omega*t)*1i)/(L^(1/2)*rho^(1/2)))*1i)/(4*k^(1/2)*rho^(1/2)*(omega^2 - (2*k)/(L*rho))) - (2^(1/2)*L^(1/2)*p0*exp((2^(1/2)*k^(1/2)*t*1i)/(L^(1/2)*rho^(1/2)))*exp(-(2^(1/2)*t*(-L*k*rho)^(1/2))/(L*rho))*(omega*sin(omega*t) + (2^(1/2)*k^(1/2)*cos(omega*t)*1i)/(L^(1/2)*rho^(1/2)))*1i)/(4*k^(1/2)*rho^(1/2)*(omega^2 - (2*k)/(L*rho)))

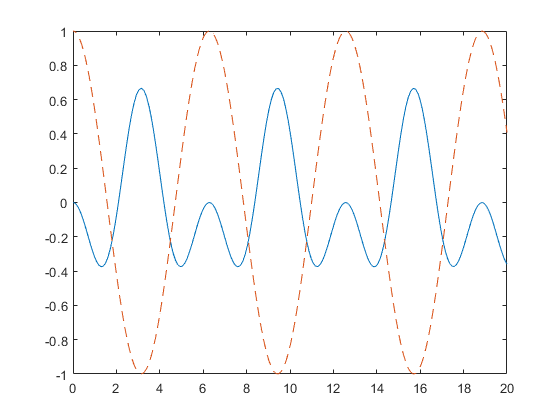
Solve the forced harmonic oscillator numerically

w'' + 2k/(rho*L)*w = -p0/rho*cos(omega*t)

% y = [w(t), w'(t)]
k = 2;
rho = 1;
L = 1;
p0 = 1;
omega = 1;
myode = @(t,y) [y(2); -2*k/(rho*L)*y(1)-p0/rho*cos(omega*t)];
[t, Y] = ode45(myode,[0 20],[0 0]);
hold off
plot(t,Y(:,1),t,cos(omega*t),'--')

Published with MATLAB® R2024a