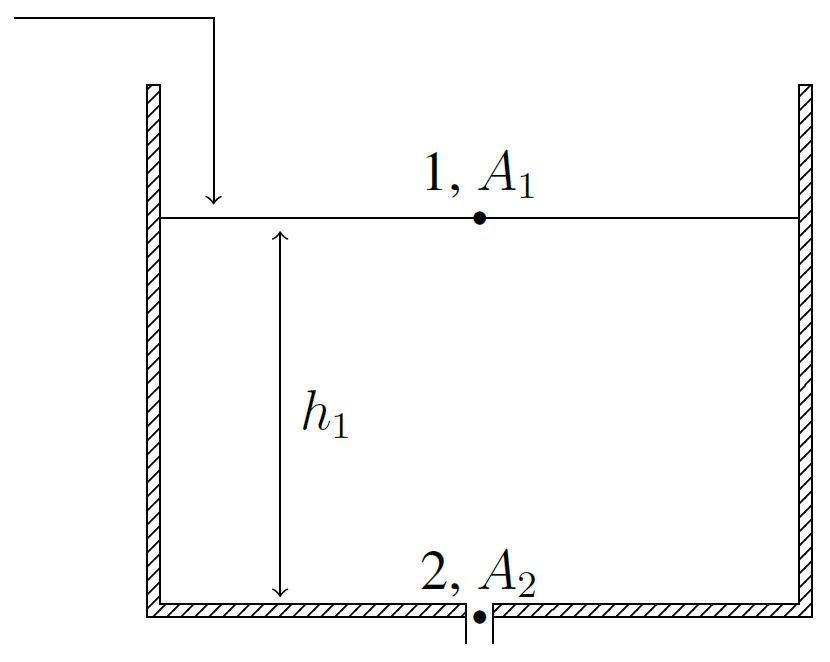
Consider a tank of cross sectional area $A_1$ containing a liquid to a height $h_1$, which flows from the bottom of the tank through a small hole of area $A_2$, as shown below,

Apply Bernoulli's Equation between points 1 and 2.
$$\frac{P_1}{\rho_1g}+\frac{u_1^2}{2g}+h_1=\frac{P_2}{\rho_2g}+\frac{u_2^2}{2g}+h_2+\Delta\,h_f$$
Assumptions:
- Ideal (frictionless) flow; $\Delta\,h_f = 0$
- $u_1 = 0$ (because of the large area of $A_1$ compared with $A_2$, the velocity at point 1 is negligible compared with the velocity at point 2)
- $h_2 = 0$ (datum point is chosen at $h_2$)
- $P_1 = P_2 = P_{\text{atm}}$, both the top surface and the liquid discharging through the hole are at atmospheric pressure
Therefore,
$$u_2=\sqrt{2gh_1}$$
The volumetric flowrate of fluid through the hole is then given by,
$$Q=C_Du_2A_2=C_DA_2\sqrt{2gh_1}$$
Where $C_D$ is an empirically determined discharge coefficient as in practice friction effects arising from the fluid's viscosity will not be negligible.
In the situation in which the tank is emptying and/or liquid is added to the top then $h_1$ is no longer constant, the varying flowrate can be described, and
the liquid height determined. Note that this is now an unsteady state situation, such that,
$$Q_{in} - Q = \frac{\text{d}\,A_1h_1}{\text{d}\,t}$$
$$Q_{in} - C_DA_2\sqrt{2gh_1} = \frac{\text{d}\,A_1h_1}{\text{d}\,t}$$
The graph below allows examination of this equation.