An efficient image enhancement algorithm for ImAGES
OF steel reinforcing bars in concrete obtained
by a new solid state sensor based
system
Sensing,
Imaging and Signal Processing Group (SISP),
School of
Electrical and Electronic Engineering.
The University of
Manchester, PO Box 88, Manchester M60 1QD, United Kingdom
ABSTRACT. This paper describes a new image
processing method capable of enhancing the raw images of steel reinforcing bars
in concrete obtained by a new generation of imaging instrument based on
solid-state magneto-inductive
(MI) sensors. The new method considers the non uniform response of the static
search coil and addresses the problem of image blurring due to bar depth. Experimental
results obtained for different steel bars specimens are presented showing
a significant enhancement of the original image information.
Keywords: Inductive sensor, GMI, Metal detection, Image
enhancement
INTRODUCTION
Over the past decade our research group has developed several systems capable of imaging steel reinforced
bars embedded in concrete structures [1-3]. In early laboratory electromagnetic
induction-based instruments, the image was formed by performing a 2D scanning
over the concrete surface. In such configurations, the excitation coil travels
with the sensor during the scanning process therefore producing a constant magnetic
flux density at each of the scanned position; the flux distribution is uniform
through the entire scanned area, which in turn results in constant curvilinear
sensor response to the magnetic field perturbation over distance and a constant
baseline or sensor reference for each line scan as shown in Figure 1. Recently,
we have also developed a new generation of imaging instrument based on
commercially available solid-state magneto-inductive
(MI) sensors for imaging steel reinforcing bars in concrete [4]. In the
later, however, the magnetic flux is produced by a static coil while the
intensity of the magnetic flux distribution and its interaction with the
metallic targets is measured by an array of fix MI sensors travelling in only
one direction during the scanning. This result in a nonlinear and non-uniform
sensor measurement with different baseline and sensor reference for each line
scan as a consequence of the non-uniform magnetic flux distribution associated
with the coil and therefore requires a new kind of image processing algorithms
to both separate the different layers and to de-blur the composite image. The
2D raw images obtained by scanning system in general are blurred in nature, due
to their blur function or point spread function. In this case, the blurring
gets even worse due to the non-uniformity of the coil flux density and it
increases with depth. Additionally, in a bar mesh, deeper bars appear fainted
than those close to the surface due to the weaker signal that they generate
specially when the image is normalize in relation to the strong signal returned
form the upper bars [5]. Furthermore, additional noise has also been introduced
to the readings by the minor misalignment of the surface mounting solid-state
sensors in the sensor array PCB fabrication.
Several methods have been employed in the past for
the case of uniform flux distribution including image subtraction [1],
deconvolution [6], Hough transform [7] and polynomial-based layer separation [5]
methods. The method described here, however, considers the non-uniform sensor reading
response due to the static coil flux density and initial results suggest
superior performance to other comparables techniques. A block diagram of the
proposed new algorithm is show in Figure 2 and explained in detail in the
following sections.
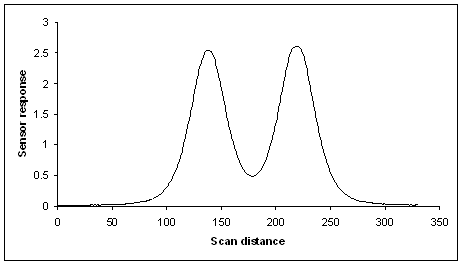
Figure
1. Typical line
scan of two bars obtained by a laboratory electromagnetic induction-based
instrument. The sensor reference level is the same at the begging and end of
the scan line.
METHOD
In order to generate an image, the sensor array is
scanned in only one direction by a
laboratory-based motorized scanner controlled with a computer across the surface of concrete
sample which contains the bar mesh. A scan step of 0.96 mm was used in the moving axis. For algorithm
explanation purposes in this paper, we will consider the origin of coordinates in
the scanned image located at the top left corner, and that the scan process has
stared at the top of the image, the linear sensor array contains 33 single
sensing elements spaced a 10 mm each [4] starting from left to right, assuming
that the sensor array was oriented in the horizontal direction and that the
scan was performed along the vertical direction from top to bottom in relation
to the centre of the image, the result is a 2D matrix with 33 x 33 individual
sensor readings at well defined space locations with each row representing a
single line scan taken by the linear sensor array. To interpret the scanned
signal this matrix can be mapped to a 256-bit grey scale image using a
proportional linear transformation to generate a low resolution image with
33x33 pixels, which can be increased in resolution using image interpolation
techniques, as described in [8].
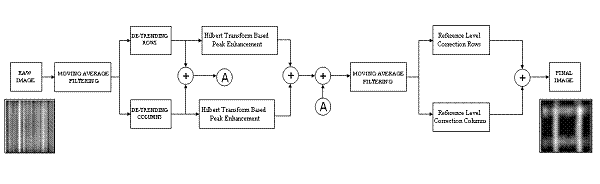
Figure
2. Block Diagram of
the proposed method of image enhancement.
Figure 3 shows a typical low resolution image
obtained after scanning the sensor array across a sample containing a bar mesh which have two 12 mm
diameter bars in the top and bottom layers and positioned at 100 mm depth from
the plane of the sensor array as shown in Figure 4. It is
clear from the image shown in Figure 2 that the raw image has a high degree of noise and blurring, and
therefore it is very difficult to interpret and analyze, the bottom and top
layers of the mesh are barely discernable.

Figure 3. Low resolution raw image.

Figure 4. Experimental Setup.
As shown in the block
diagram of Figure 2, a smoothing algorithm, such as the method of moving
averages or a low pass filtering [9] is used for pre-processing each row of the
raw image in order to
Further enhancement to the image can be obtained by
combining the image of Figure 7c with an image obtained after processing the same
image with an peak enhance algorithm based in the Hilbert transform [11].
Figure 8 show the image resulting of the peak enhance algorithm and Figure 9
shows the image obtained by combining the image of Figure 7c and Figure 8.
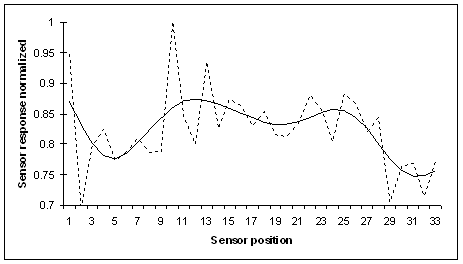
Figure 5. Typical sensor array reading at the middle of the scan
image, the dash line show the actual sensor readings and the solid line show
the reading after misalignment correction by moving averaging filtering. The
sensor response has been normalized to the maximum reading of the array.

Figure 6. Raw image after filtering.
|
(a) vertical components |
(b) horizontal components |
(c) image after de-trending |
|
|
|
|
Figure 7. Images obtained after passing trough the de-trending
algorithm.

Figure 8. Image after Hilbert transform based peak enhance algorithm.

Figure 9. Images obtained after combining images of Figues 7 and 6c.
A moving average filter is then used again in order
to remove any noise further introduced to the image by the de-trending and peak
enhancement algorithms. The Image obtained after all this process is shown in
Figure 10. By comparing this image with the original raw image of Figure 3, it
is clear that a significant improvement has been achieved in terms of image quality;
however, some degree of blurring is still remaining in the image. This is
mainly due to the non-constant and non-uniform reference level of each
individual row of the processed image so far as shown in Figure 11. In Figure 11,
each peak represents the presents of a metallic bar in each line scan, however,
notice in this case that the bell type curve of each peak has different
starting and ending points for each line scan, this differs from the typical
line scan previously obtained by scanning configurations were the exciting coil
travels with the sensor produces a curvilinear sensor response to the magnetic
field perturbation over distance and a constant baseline and sensor reference
for each line scan as shown in Figure 1.
The broadening effect of the peak increase with depth which contributes to the
blurring of the image, in the case of the sensor array this effect is more
severe since the sensor reference is different for each line scan as shown in Figure
11. However, it is possible to remove
this unwanted blurring of the image by removing information form each
individual line scan according with a threshold level set at 0, this threshold
level will compensate the non-uniform
sensor reference level of the line scan readings. This correction should be
applied to both rows and columns of the image. Figure 12 shows the final de-blur
image after sensors refence level correction and interpolated to a 320x320
pixels resolution. In this image the top and bottom bars of the bar mesh are
now clearly discernible and the improvement in relation to the raw image of
Figures 3 and 6 is quit remarkable.

Figure 10. Image after
further filtering of image in Figure 9.
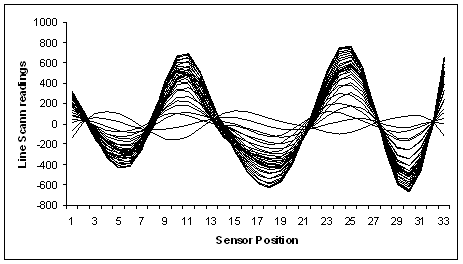
Figure 11. Individual rows of image of Figure 9, plotted as
individual line array readings. Each line scan has different baseline and
different staring and ending points.

Figure 12. Final Image
after further processing of image in Figure 11.
RESULTS AND DISCUSSION
Several scans of bar mesh configuration with bars of
different diameters at different distances were conducted with a sensor array
system and the obtained raw images were processed using the new image
processing algorithm in order to determine its performance. Figure 13 shows the
images obtained before and after processing. The images shown are high-resolution
320 ´ 320 pixel images generated by applying image interpolation
techniques to the original low resolution 33x33 pixel images generated by the scanner.
It can be seen from the results obtained in Figure 13 that a
remarkable improvement in the image quality has been obtained in each case, by
using the processed with the proposed algorithm the images information content
of each image has been enhanced and therefore the original structures are now clearly
visible and discernible. Although complex, the algorithm is relatively easy to
implement and it is an essential precursor in the development of a real time
scanner which will generate real video of the rebar structures. With minor
modifications it can also be applied to de-blur images obtained by previous
laboratory electromagnetic induction-based instruments.
|
Sample
mesh |
Raw Image |
Final
Image |
|
12 mm bars at 100 mm depth |
|
|
|
12 mm bars at 100 mm depth |
|
|
|
12 mm bars at 100 mm depth |
|
|
|
12 mm bars at 110 mm depth |
|
|
|
10 mm bars at 100 mm depth |
|
|
|
12 mm bars at 70 mm depth |
|
|
Figure 13. Image obtained by scanning different bar mesh
configurations at different depths. The raw and processed images are shown in
320X320 pixels resolution.
CONCLUSION
A new method has been developed for image enhancement of steel reinforcing in concrete
obtained by a sensor array based sensor. Experimental
results show that the method is not only robust and repeatable but also
computationally efficient; it can also accommodate different depths and
configurations. The new method considers the non-uniform sensor array readings response due to the
static coil flux density and the results obtained suggest superior performance
to previous techniques.
ACKNOWLEDGEMENT
The authors wish to express their gratitude to
the Engineering and
Physical Sciences Research Council in the UK for
financially supporting this work.
REFERENCES
1. P. Gaydecki, and F.
Burdekin, “An inductive scanning system for two dimensional imaging of
reinforcing components in concrete structures”, Measurements Science and Technology, vol. 5, 1994, pp. 1272-1280.
2.
G. Miller, P. Gaydecki, S. Quek, B. Fernandes and M. Zaid, “A combined Q and heterodyne sensor
incorporating real-time DSP for reinforcement imaging,
corrosion detection and material characterization”, Sensors and Actuators A: Physical, vol. 121, Issue 2, June 30,
2005, pp. 339-346.
3.
P. Gaydecki, S. Quek, G. Miller, B. Fernandes and M. Zaid, “Design
and evaluation of an inductive Q-detection sensor
incorporating DSP for imaging of steel reinforcing bars in concrete”, Measurements Science and
Technology, vol. 13, 2002, pp.
1327-35.
4.
D. Benitez, S. Quek, P. Gaydecki, and V. Torres, “ A 1D Solid state sensor based array system for real time
magnetic field imaging of steel reinforcing bars embedded within reinforced
concrete”, IEEE Trans. Instrum. Meas. (submitted).
5. S. Quek, P. Gaydecki, B. Fernandes, G. Miller,
“Multiple layer separation and visualization of inductively scanned images of reinforcing bars in concrete using polynomial-based
separation algorithm”, NDT&E
international, 35, 233–240 (2002).
6. P. Gaydecki, K.
Glossop and F. Burdekin, “A prototype inductive scanning system for
two-dimensional imaging of metal reinforcing components in concrete system
design and data visualization”, The International Symposium of NDT
in Civil Engineering (NDT-CE) in Berlin, Germany, September Vol.1, 1995, pp. 745-752.
7. B. Fernandes, I. Silva, P. Gaydecki, “Vector
extraction from digital images of steel bars
produced by an inductive scanning system using a differential gradient method combined
with a modified hough transform”, NDT&E
international, 33, 69–75 (2000).
8.
M.
Zaid, P. Gaydecki, S. Quek, G. Miller and B. Fernandes, “Image reconstruction
of steel reinforcing bars in concrete using fourier-domain interpolation
applied to a sparsely populated data set”, Journal of Nondestructive
Evaluation, vol. 18,
No.3-4, September-December, 2002, pp. 119-130.
9. C. Chatfield, “The analysis of time
series”, 6th Edition, CRC press, 2004.
10. R. Shumway, D. Stoffer, “Time series
analysis and its applications”, Springer-Verlag, 2000.
11. D. Benitez D, P. Gaydecki, A. Zaidi,
A. Fitzpatrick, “The Use of the Hilbert Transform in ECG Signal Analysis”, Computers in Biology and Medicine, 31,
pp. 399-406.














