Opposite wall contact and higher buckling modes
The previous pages demonstrated the
existence of small-volume liquid bridges in strongly buckled
elastic tubes. Here we investigate what happens if we start
with an axisymmetric liquid bridge (formed, e.g., via Halpern &
Grotberg's primary axisymmetric
instability):
Once the liquid bridge is formed, the system becomes statically unstable
to non-axisymmetric perturbations and the tube buckles while
spreading out the fluid contained in the liquid bridge.
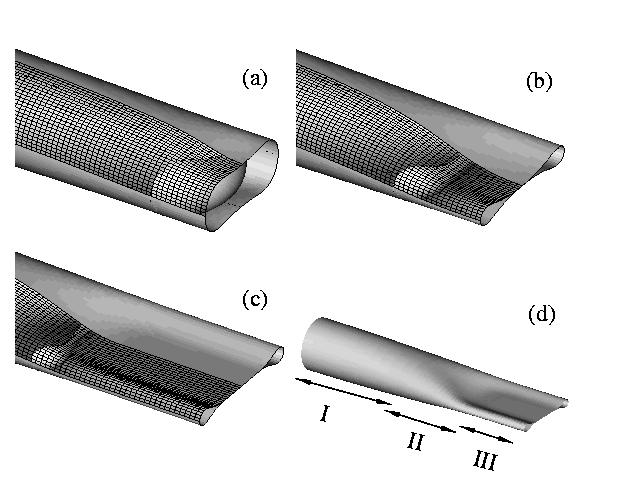
The figure below shows a quasi-static (!) sequence of this buckling
process. Note that the intermediate (slightly buckled) states are
actually unstable themselves -- only the strongly collapsed configuration
with opposite wall contact, shown in (c) and (d), is stable. [For the
mathematically inclined readers: This is because the buckling
takes place by a subcritical bifurcation.]
For sufficiently high surface tension of the liquid bridge
we can also get buckling with higher circumferential wavenumbers.
Here's an example of a tube that is buckling into three lobes:
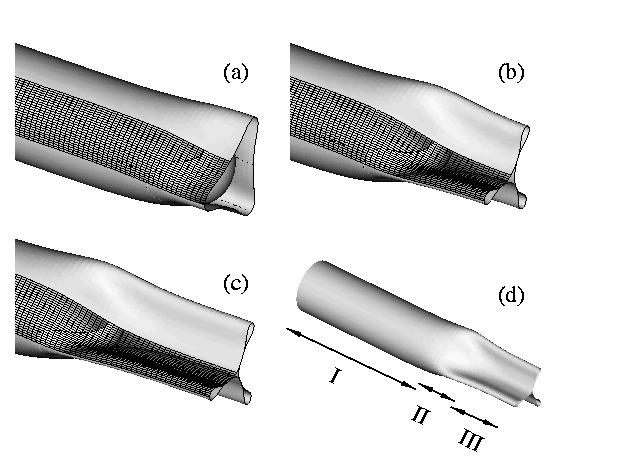
Note that the shape of the air-liquid interface is quite different
from that in the two-lobed collapse shown above. Physiological
observations suggest that airway closure actually takes place
in such multiple lobes.
Back to
`Airway Closure'.
Page last modified: September 29, 2000
Back to Matthias Heil's home page..


