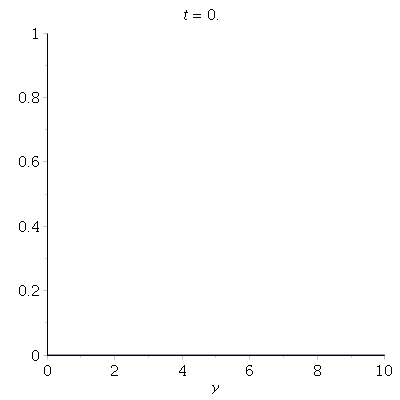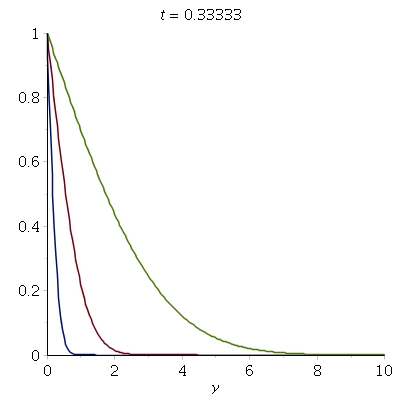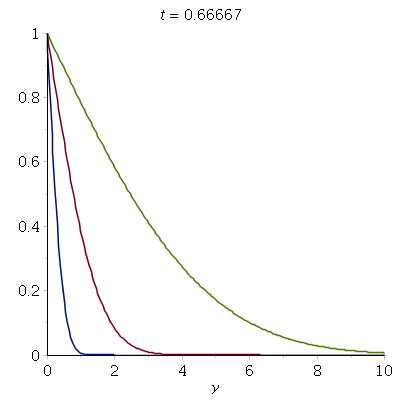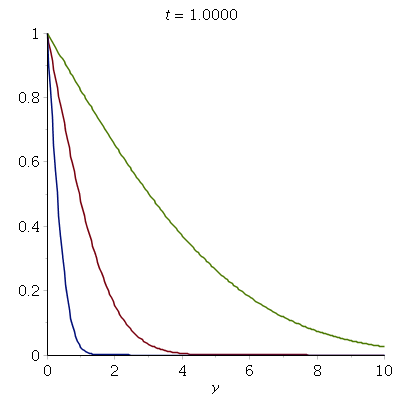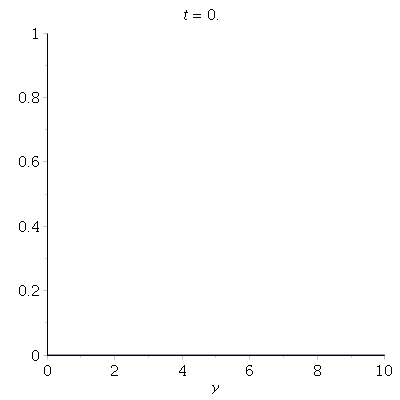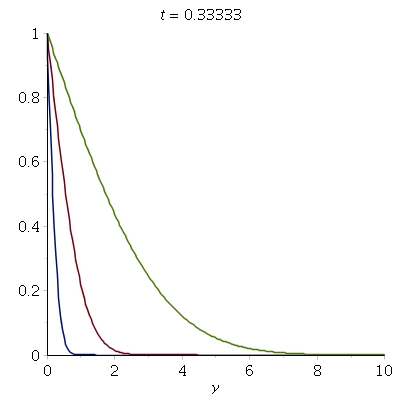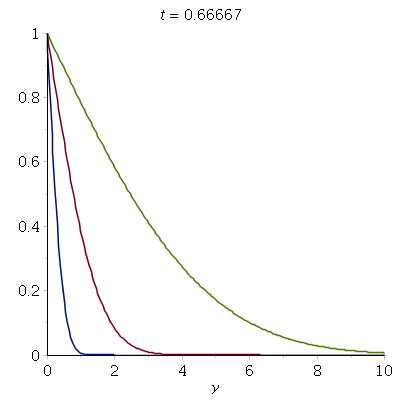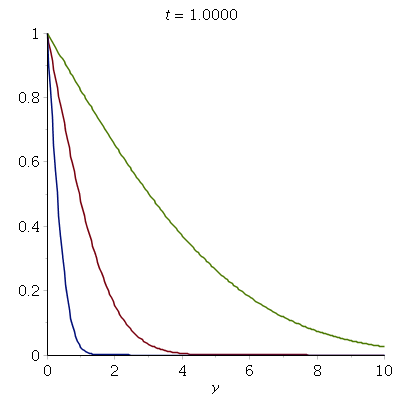MATH35001: Animation of flow field above impulsively
started plate
Here's an animation of the flow field u(y,t) above an impulsively
started plate:
u(y,t) = U erfc(1/2 y/sqrt(nu t))
The animation shows u/U (so the maximum is one) as a function of y for
increasing time.
The different lines illustrate the effect of varying the
(kinematic) viscosity nu. Blue: nu=0.1; Red: nu=1.0; Green: nu=10.0.
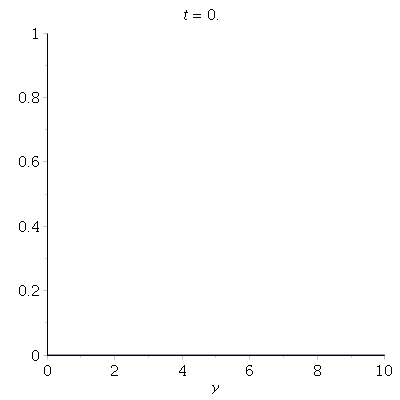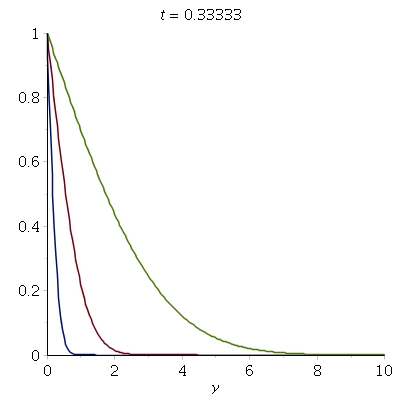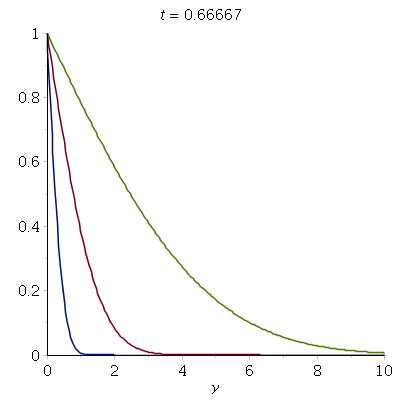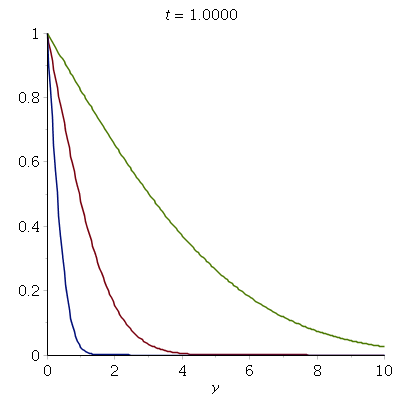Recall that nu = mu / rho, so large values of nu correspond to
a large (dynamic) viscosity mu or, equivalently, a small density rho.
This explains why the velocity imposed by the suddenly started plate
(at t=0) propagates (diffuses!) more quickly into the domain
for larger nu: the fluid is more "sticky" but has little inertia,
therefore the plate rapidly drags a large amount of fluid with it.
This is because the fluid "doesn't mind" being
accelerated (because it is light) but ideally each layer of fluid
wants to have the same velocity as its neighbours (because the
large viscosity generates large shear stresses between layers that
move at different velocities).
Conversely, for small values of nu, the viscosity of the fluid
is so small that even large velocity gradients only generate moderate
shear stresses between adjacent layers of fluid which ideally want to stay at
rest -- because of their large inertia. Hence, it takes much
longer for the velocity imposed by the plate to propagate (diffuse)
into the fluid.
Page last modified: November 24, 2017
Back to Matthias Heil's home page..