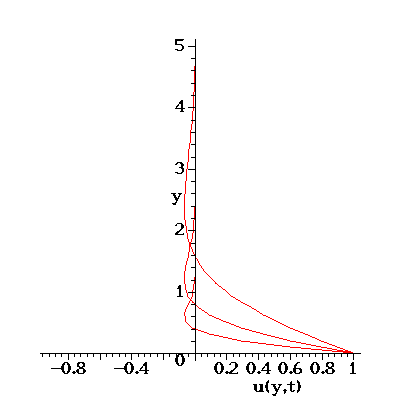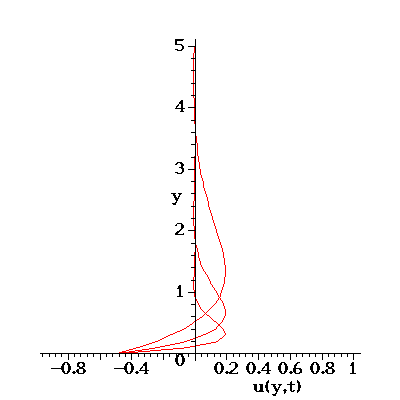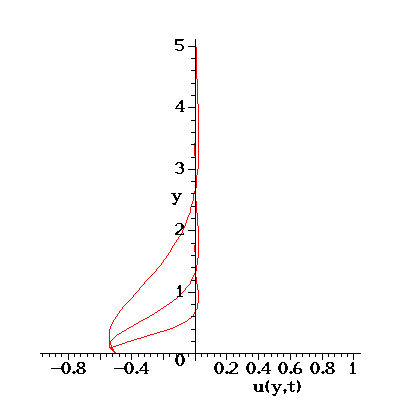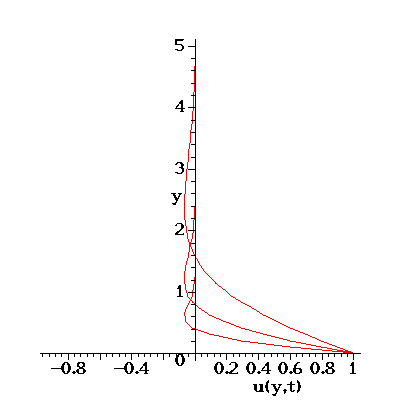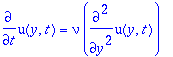
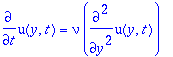
The plate oscillates in the plane y=0 and the velocity boundary condition is given by
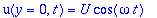
The periodic solution for U=1 which is animated below is
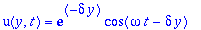
where
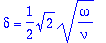
Three velocity profiles are shown: They represent the solutions for
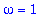 and for
and for
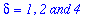 .
In all cases the velocity decays to zero as one moves away from the
oscillating plate. For larger values of
.
In all cases the velocity decays to zero as one moves away from the
oscillating plate. For larger values of 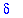 (corresponding to, e.g., a high frequency oscillation of the plate) the flow is
dominated by inertial effects and the perturbation to the flow field
is restricted to a shallow layer near the moving plate
-- the fluid's inertia wants to keep the fluid at rest.
For smaller values
of
(corresponding to, e.g., a high frequency oscillation of the plate) the flow is
dominated by inertial effects and the perturbation to the flow field
is restricted to a shallow layer near the moving plate
-- the fluid's inertia wants to keep the fluid at rest.
For smaller values
of 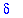 (corresponding to low frequency oscillations or large viscosity)
viscous effects dominate and the velocity perturbation caused by the
moving plate is felt further inside the bulk of the fluid -- due to
the large viscosity, the plate can drag `more' fluid with it.
Therefore the velocity perturbation decays more slowly as one moves
away from the plate.
(corresponding to low frequency oscillations or large viscosity)
viscous effects dominate and the velocity perturbation caused by the
moving plate is felt further inside the bulk of the fluid -- due to
the large viscosity, the plate can drag `more' fluid with it.
Therefore the velocity perturbation decays more slowly as one moves
away from the plate.