>

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

> > #----------------------------------------------------------------------- # Let's try the first-order ODE where I dropped the mod sign on the LHS: #----------------------------------------------------------------------- > ode:=y*diff(v(y),y)-(2*v(y)-2);
> soln:=dsolve(ode,v(y));
> > #----------------------------------------------------------------------- # Go figure! (Consider the two cases for the mod separately; turns out # the above is "general"; we just drop the assumption on the constant # being positive! #----------------------------------------------------------------------- > ######################################################################## > #----------------------------------------------------------------------- # Full ODE: Note Maple misses the "other" family of solutions: constants #----------------------------------------------------------------------- > ode2:=y(x)*diff(y(x),x$2)-2*diff(y(x),x)^2-2*diff(y(x),x);
> > soln2:=dsolve(ode2,y(x));
> > #----------------------------------------------------------------------- # Look: constants solve the ODE too! Maple, you are stupid! #----------------------------------------------------------------------- > y_test:=A;
> eval(subs(y(x)=y_test,ode2));
> > > #----------------------------------------------------------------------- # Does the "general" (not!) solution obtained by maple approach a # constant for extreme values of one of the constants? Obviously only # _C1 has the potential to do this since _C2 just shifts the origin of x. #----------------------------------------------------------------------- > assign(soln2); > plot({subs(_C2 = 1, _C1 = 0.1, y(x)), >       subs(_C2 = 1, _C1 = 1, y(x)), >       subs(_C2 = 1, _C1 = 10, y(x))}, >       x = -5 .. 5);
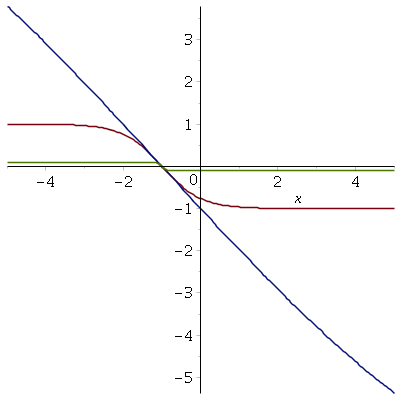> > plot(subs(_C2 = 1, _C1 = 100, y(x)), >       x = -5 .. 5);
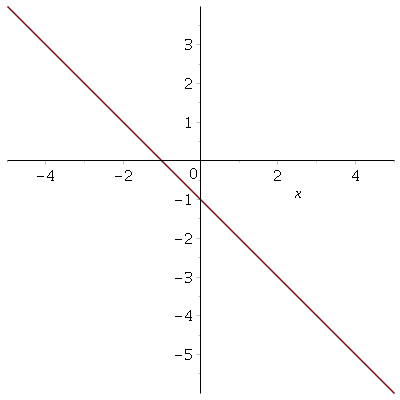> #----------------------------------------------------------------------- # Doesn't look promising... Let's consider the formal limits: #----------------------------------------------------------------------- > limit(y(x), _C1 =  infinity);
> limit(y(x), _C1 = -infinity);
> limit(y(x), _C1 = 0);
>

 

>