Current-induced
Orbital Magnetization in noncentrosymmetic systems
In systems with time-reversal symmetry, the orbital magnetization is zero in equilibrium. Recently, it has been proposed that the orbital magnetization can be induced by an electric current in a helical crystal structure in the same manner as that in a classical solenoid. In this paper, we extend this theory and study the current-induced orbital magnetization in a broader class of systems without inversion symmetry. First, we consider polar metals which have no inversion symmetry. We find that the current-induced orbital magnetization appears in a direction perpendicular to the electric current even without spin-orbit coupling. Using the perturbation method, we physically clarify how the current-induced orbital magnetization appears in polar metals. As an example, we calculate the current-induced orbital magnetization in SnP and find that it might be sufficiently large for measurement. Next, we consider a two-dimensional system without inversion symmetry. We establish a method to calculate the current-induced orbital magnetization in the in-plane direction by using real-space coordinates in the thickness direction. By applying this theory to surfaces and interfaces of insulators, we find that an electric current along surfaces and interfaces induces an orbital magnetization perpendicular to the electric current.
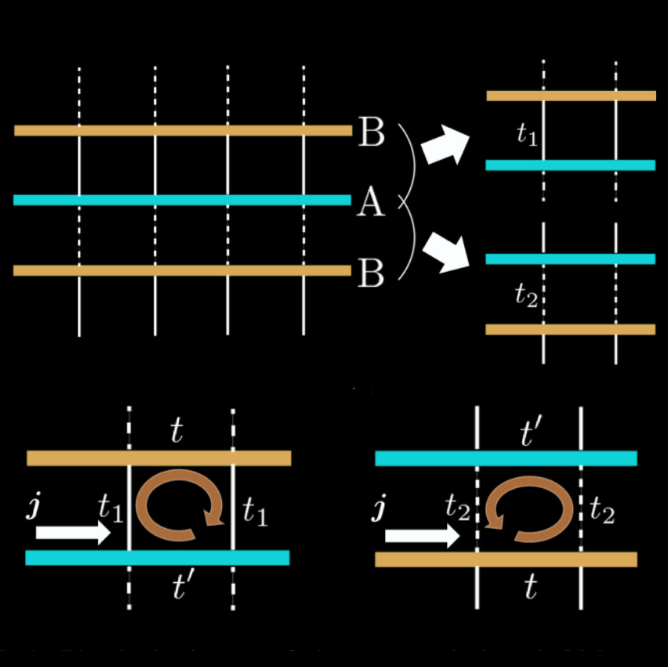
Physical picture of the current-induced OM. (Top panel) Two types of pairs of neighboring layers. We assume that the hopping (t) within the B layers (blue) is different from that (t') within the A layers (red). This model has two combinations of neighboring layers. One is including t1 , and the other is including t2 . (bottom panels) Closed loops of an electric current. Due to this difference of the interlayer hoppings, we expect that the OM will appear. The orientation of the current-induced OM within the two neighboring layers is reversed because the relative positions between t and t# are reversed.

