J. D. Jackson
Reynolds the Scientist
This initial stream of Reynolds' work, which was described in the terms
used above by his most famous student, J.J. Thomson, clearly stemmed
from interests developed as a result of his background and experience
prior to coming to Manchester. It was convenient as an initial area for
research in view of the fact that little was available to him at that
time in the way of laboratory and workshop facilities at Owens College.
In addition it provided ideal material for lectures of general interest
and popular appeal for presentation to the Manchester Literary and
Philosophical Society.
The papers on this aspect of his work, which are all to be found in
Volume I of the Collected Works, deal with matters concerned with
comets; the solar corona and the aurora; terrestrial magnetism; the
electrical properties of clouds; the bursting of trees struck by
lightning; the destruction of sound by fog; the refraction of sound by
the atmosphere; the action of rain to calm the sea; the action of oil
on water in preventing wind waves; surface tension and capillary action.
Back to Contents
 The earliest of these,
Papers 2, 3A and 3B (1870-1872), are all closely
related. In Papers 2 and 3A the tails of comets, the solar corona and
the aurora are considered as electrical phenomena. In Paper 3B (1872),
a corona resembling the solar corona produced by discharging electricity
from a brass ball in a partially evacuated receiver is described (see
Figure 1). In Paper 4 (1872), the induction of static electricity on the
part of the sun is proposed as a probable cause of terrestrial magnetism
and in Paper 5 (1872) the inductive action of the sun on the electrical
properties of clouds is considered with respect to thunderstorms.
Paper 7 (1873) `On the bursting of trees and other objects struck by lightning'
reports an experiment showing that the explosive effect of a lightning
strike is due to the rapid evaporation of moisture into steam.
The earliest of these,
Papers 2, 3A and 3B (1870-1872), are all closely
related. In Papers 2 and 3A the tails of comets, the solar corona and
the aurora are considered as electrical phenomena. In Paper 3B (1872),
a corona resembling the solar corona produced by discharging electricity
from a brass ball in a partially evacuated receiver is described (see
Figure 1). In Paper 4 (1872), the induction of static electricity on the
part of the sun is proposed as a probable cause of terrestrial magnetism
and in Paper 5 (1872) the inductive action of the sun on the electrical
properties of clouds is considered with respect to thunderstorms.
Paper 7 (1873) `On the bursting of trees and other objects struck by lightning'
reports an experiment showing that the explosive effect of a lightning
strike is due to the rapid evaporation of moisture into steam.
Back to Contents
In Paper 7A (1873) Reynolds deals with the destruction of sound by fog
explaining it in terms of the resistance to motion of air when charged
with small droplets of water.
Paper 16 (1874) and Paper 22 (1876) are likewise concerned with the
refraction of sound by the atmosphere. In these Reynolds considers the
effects due to the difference of wind velocity near the surface of the
ground and at a height above it. This causes sound to be lifted when
the waves move into the wind and to fall when waves move with the wind.
He goes on to examine the effect of the variation of temperature in the
atmosphere and explains that this causes sound waves to rise.
Experiments are reported in which he studied these various effects but
the papers are particularly noteworthy for the keenness of Reynolds'
observations and revealing of his interest in outdoor pursuits. Thus:
`It has often astonished me, however, when shooting, that a wind which
did not appear to me to make the least difference to the direction in
which I could hear small sounds distinctly, should yet be sufficient to
cover one's approach to partridges, and more particularly to rabbits,
even until one was within a few feet of them - a fact which shows how
much more effectively the wind obstructs sound near the ground than even
a few feet above it.'
 In a presentation to the Manchester Literary and Philosophical Society,
`On the action of rain to calm the sea' (Paper 15, 1875) Reynolds showed
by experiment that vortex rings produced by droplets of rain cause water
to be carried well below the surface in appreciable amounts leading to
the damping of wave motion (see Figure 2).
In a presentation to the Manchester Literary and Philosophical Society,
`On the action of rain to calm the sea' (Paper 15, 1875) Reynolds showed
by experiment that vortex rings produced by droplets of rain cause water
to be carried well below the surface in appreciable amounts leading to
the damping of wave motion (see Figure 2).
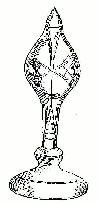
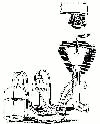 Papers 29 (1875) and 30 (1877) deal with the formation of raindrops,
hailstones and snowflakes. Reynolds points out that hailstones are
formed by the aggregation of small frozen particles resulting from
coalescence with more rapidly descending larger particles. To prove it
he ingeniously produced artificial hailstones by chilling a flow of air
laden with tiny droplets of water through the use of an ether spray (see
Figure 3).
Papers 29 (1875) and 30 (1877) deal with the formation of raindrops,
hailstones and snowflakes. Reynolds points out that hailstones are
formed by the aggregation of small frozen particles resulting from
coalescence with more rapidly descending larger particles. To prove it
he ingeniously produced artificial hailstones by chilling a flow of air
laden with tiny droplets of water through the use of an ether spray (see
Figure 3).
In a paper read to the British Association in 1880 `On the effect of oil
in destroying waves on the surface of water' (Paper 38), Reynolds
attributes this to the surface tension varying inversely with the
thickness of the oil film as the wind flows over it. This introduces
tangential stiffness which prevents the surface taking up the motion of
the water beneath. The effect is a dynamic one; instead of wave motion
occurring in the water, eddies are formed below the surface. At the
centennial British Association meeting held at York the following year
Reynolds developed his ideas `On surface-tension and capillary action'
still further (Paper 39).
On October 4th 1881 Reynolds made a short presentation to the Manchester
Literary and Philosophical Society `On the floating of drops on the
surface of water depending only on the purity of the surface'
(Paper 40).
In this Reynolds reported experiments using powder in the form of
flowers of sulphur to determine the circumstances under which such drops
are suspended.
Back to Contents
This is a part of Osborne Reynolds' work which is not as widely
appreciated now as it deserves to be. It was, however, of considerable
interest within the Victorian scientific community and it was for his
early efforts in this area that Reynolds was elected a Fellow of the
Royal Society in 1877. Featuring in both Volumes I and II of the
Collected Works, his papers deal with forces at a surface caused by
evaporation; condensation and heat transfer; the transpiration of gases
through porous media; the internal cohesion of liquids; the dilatancy of
granular materials and the general properties of matter. Almost all of
Reynolds' post-1877 publications on these matters were presented to the
Royal Society.
Back to Contents
In Paper 11 (1874) Reynolds is concerned with the forces due to the
evaporation or condensation of a liquid at a surface. Experiments
conducted by him showed that evaporation caused a force tending to drive
the surface back and condensation a force tending to drive the surface
forward. The explanation of these effects is given using the kinetic
theory model of gases.
 Papers 12 (1874) and 23 (1876)
deal with forces exerted by the
communication of heat to a surface immersed in a rarefied gas. Such
forces are attributed to molecular influences and used to afford an
explanation of the operation of the Crookes light mill (Figure 4), again
using the kinetic theory model. The ideas involved led Reynolds to
invent a simple photometer. Experiments on a light mill performed in
collaboration with a colleague at Owens College, Arthur Schuster,
demonstrated conclusively that the force which turns the vanes is not
directly due to thermal radiation.
Papers 12 (1874) and 23 (1876)
deal with forces exerted by the
communication of heat to a surface immersed in a rarefied gas. Such
forces are attributed to molecular influences and used to afford an
explanation of the operation of the Crookes light mill (Figure 4), again
using the kinetic theory model. The ideas involved led Reynolds to
invent a simple photometer. Experiments on a light mill performed in
collaboration with a colleague at Owens College, Arthur Schuster,
demonstrated conclusively that the force which turns the vanes is not
directly due to thermal radiation.
 Reynolds' interest in the Crookes light mill was perhaps the initial
stimulus for his thoughts on the so-called `transpiration' of gases.
Graham had applied this term to the passage of gases through capillary
tubes. Reynolds re-applied it to describe the motion of gases through
minute channels including porous plugs and apertures in thin plates as
well as capillary tubes. The results of his 1879 investigation are
presented in one of the longest and most original of his papers entitled
`On Certain Dimensional Properties of Matter in the Gaseous State'
(Paper 33). In this, he showed by theory and experiment (using the
apparatus shown in Figures 5a and 5b) that not only would a difference
of pressure cause a gas to flow from one side of a porous plate to the
other, but so also would a difference of temperature, even when initially
the pressures on the two sides were equal. To this phenomenon he gave
the name `thermal transpiration'.
Reynolds' interest in the Crookes light mill was perhaps the initial
stimulus for his thoughts on the so-called `transpiration' of gases.
Graham had applied this term to the passage of gases through capillary
tubes. Reynolds re-applied it to describe the motion of gases through
minute channels including porous plugs and apertures in thin plates as
well as capillary tubes. The results of his 1879 investigation are
presented in one of the longest and most original of his papers entitled
`On Certain Dimensional Properties of Matter in the Gaseous State'
(Paper 33). In this, he showed by theory and experiment (using the
apparatus shown in Figures 5a and 5b) that not only would a difference
of pressure cause a gas to flow from one side of a porous plate to the
other, but so also would a difference of temperature, even when initially
the pressures on the two sides were equal. To this phenomenon he gave
the name `thermal transpiration'.
 In the same paper Reynolds also demonstrated that the extremely low
pressure of the gas in the light mill was necessary because of the
comparatively large size of the vanes and that similar results ought to
be obtainable with smaller vanes at higher pressure. This he proved by
experiments on fibres of silk and a `spider line' using the apparatus in
Figure 6. He showed that, provided the pressure in the vessel containing
the fibre was not more than approximately one-quarter of an atmosphere,
the fibre moved towards an external source of heat.
In the same paper Reynolds also demonstrated that the extremely low
pressure of the gas in the light mill was necessary because of the
comparatively large size of the vanes and that similar results ought to
be obtainable with smaller vanes at higher pressure. This he proved by
experiments on fibres of silk and a `spider line' using the apparatus in
Figure 6. He showed that, provided the pressure in the vessel containing
the fibre was not more than approximately one-quarter of an atmosphere,
the fibre moved towards an external source of heat.
Reynolds considered his investigation as a whole to have very profound
implications, affording a proof that gas is not a continuous medium but
possesses a `dimensional structure'. His description and explanation
introduced the dependence of the density of the gas in relation to the
size of the passages in the porous medium or the vanes of the light mill,
and so involved what he called the `dimensional properties of gases'.
This he believed could have more than philosophical importance:
`The actions only become considerable within extremely small spaces, but
then the work of construction in the animal and vegetable world, and the
work of destruction in the mineral world, are carried on within such
spaces. The varying action of the sun must be to cause alternate
inspiration and expiration of air, promoting continual change of air
within the interstices of the soil as well as within the tissue of
plants. What may be the effects of such changes we do not know, but the
changes go on; and we may fairly assume that in the processes of nature
the dimensional properties of gas play no unimportant part.'
Advancement of the kinetic theory of gases was a notable feature of the
science of the 1870s and one to which Reynolds made a significant
contribution alongside more established figures such as Maxwell. A short
note by Reynolds on thermal transpiration (Paper 34), written in response
to a criticism of his ideas by Maxwell and communicated to the Royal
Society by its Secretary Sir George Stokes in 1879, provides an
intriguing insight into the very formal manner in which the scientific
establishment operated.
Reynolds' work on the surface forces due to heating and on thermal
transpiration provided valuable experimental support for the developing
kinetic theory (i.e. that `heat' is a manifestation of the molecules of
which a gas is composed). Widespread acceptance of the theory by the
scientific community did not come until much later. Reynolds'
experiments and theoretical contributions in the period 1874 to 1879 were
many years in advance of the time. It is of interest that one of
Reynolds' students in his last years at Manchester, Sidney Chapman, was
later to make further important advances in this field.
Back to Contents
 Reynolds' interest in the physics of fluids extended to liquids. In
Papers 31 (1877) and 35 (1880) delivered to the Manchester Literary and
Philosophical Society he reported experiments on the internal cohesion
of mercury and water. By careful exclusion of air he was able to
suspend a column of mercury to a height of more than double that of the
barometer (see Figure 7).
Reynolds' interest in the physics of fluids extended to liquids. In
Papers 31 (1877) and 35 (1880) delivered to the Manchester Literary and
Philosophical Society he reported experiments on the internal cohesion
of mercury and water. By careful exclusion of air he was able to
suspend a column of mercury to a height of more than double that of the
barometer (see Figure 7).
Back to Contents
A few years later he turned his attention to the properties of granular
media. Reynolds' first announcement of the property of such media to
which he attached the name `dilatancy' was made to Section A of the
British Association at its meeting in Aberdeen in 1885. The paper
attracted sufficient attention for him to be asked to read it again to
Section B a few days later, and a printed version
(Paper 50) appeared in
the Philosophical Magazine in December of the same year with the title
`On the Dilatancy of Media Composed of Rigid Particles in Contact'. A
version also appeared in Nature due to the extent of interest. The
British Association audiences must have been greatly intrigued by the
strikingly simple but ingenious experiments which he performed and
equally startled by the conclusions which he drew from them.
 He applied the term `dilatancy' to the property possessed by a mass of
granular material to alter its volume in accordance with a change in the
arrangement of its grains. His illustration of this in terms of the
piling of spheres in two different ways is shown in Figure 8: the pile
of spheres in cubical formation occupies a volume greater than that of
the same number and size of spheres when piled in the second way.
He applied the term `dilatancy' to the property possessed by a mass of
granular material to alter its volume in accordance with a change in the
arrangement of its grains. His illustration of this in terms of the
piling of spheres in two different ways is shown in Figure 8: the pile
of spheres in cubical formation occupies a volume greater than that of
the same number and size of spheres when piled in the second way.
Reynolds went on to illustrate this by characteristically simple means.
If an india- rubber bottle with a glass neck is filled with water and
the bag is then squeezed, water will be forced up the neck. But if the
bottle is full of granular material and water, the effect of squeezing,
up to a point, is to draw water down from the neck into the bag, because
the grains have adopted an arrangement in which the volume of the
interstices has been increased. In Reynolds' words, `the result, but
for the knowledge of dilatancy, would appear paradoxical, not to say
magical... Sand presents many striking phenomena well known but not
hitherto explained, which are now seen to be simply evidence of
dilatancy'. A familiar phenomenon explained by Reynolds was that
observed when a foot is planted on firm moist sand on the sea- shore: an
area around the foot appears to become dry, however, when the foot is
raised, the sand beneath is found to be abnormally wet. The pressure of
the foot has increased the volume of the interstices between the grains
of sand below it and water has been drawn in to occupy the additional
voids.
Reynolds stated that the recognition of this property of dilatancy would,
from a practical point of view, place the theory of earth-pressures on a
true foundation, but that `the greatest results are likely to follow in
philosophy, and it was with a view to these results that the
investigation was undertaken'. He goes on to declare that
`the recognition of this property of dilatancy places a hitherto
unrecognized mechanical contrivance at the command of those who would
explain the fundamental arrangement of the Universe, and one which, so
far as I have been able to look into it, seems to promise great things,
besides possessing the inherent advantage of extreme simplicity.'
These were the thoughts in his mind in 1885. Indeed, the title of his
discourse to the Royal Institution in February, 1886
(Paper 51), on the
same property of granular material, contained the significant words
`possibly connected with gravitation'. Seven years previously, a
paragraph concluding his paper on dimensional properties of matter in the
gaseous state had shown that his thoughts were turning towards the
possibility of solving the riddle of the luminiferous ether. However, it
was not until February 1902, that his memoir `On the Sub- Mechanics of
the Universe' was communicated to the Royal Society.
Back to Contents
Osborne Reynolds is without doubt best known for his papers on fluid
motion and turbulence which are to be found in both Volumes I and II of
the Collected Works. The matters dealt with include: the progression of
groups of waves; vortex motion; laminar and turbulent flow in pipes; the
dynamical theory of fluid flow and, hydrodynamic lubrication. Amongst
the papers are a number which have received universal recognition.
Back to Contents
Paper 27 (1877) is concerned with the progression in deep water of groups
of dispersive surface waves and the rate at which energy is transmitted
by them. Here Reynolds showed not only that the velocity of the group is
one half that of an individual wave, as was already known, but that the
group velocity also gives the rate of transmission of energy.
Back to Contents
In the same year Reynolds described methods for rendering the internal
motions of a fluid visible by means of colour bands, a technique which
he was to use later in his renowned experiments on transition
(see below). This he did with particular reference to vortex motion,
considering the vortex lines behind an oblique wave, the vortex ring
behind an inclined disc, vortex rings caused by drops falling into water
and by a `puff' of water.
Back to Contents
In 1883, Osborne Reynolds published his famous paper entitled `An
experimental investigation of the circumstances which determine whether
motion of water shall be direct or sinuous and of the law of resistance
in parallel channels' (Paper 44). This paper, published in the
Philosophical Transactions of the Royal Society, proved to be a classic
in the literature of the science of fluid motion and had a profound
effect on the development of fluid mechanics in the widest sense. It
contained the enunciation of the dimensionless group, the Reynolds
Number.
The first step in Reynolds' discovery of this fundamental parameter
appears to have been his observation that `the tendency of water to eddy
becomes much greater as the temperature rises'. It occurred to him that
this might be related to the well-known fact that the viscosity of water
diminishes as the temperature rises, and moreover, that the physical
property, kinematic viscosity, `is a quantity of the nature of the
product of a distance and a velocity'.
He proceeded to consider the equations of motion and to establish that
the forces per unit mass are of two distinct types, inertial and viscous,
and further that the ratio of these is related to the dimensionless group
D Um/n, in which Um is the mean velocity of the flow, D is the tube
diameter and n the kinematic viscosity. In his paper he states:
`This is a definite relation of the exact kind for which I was in search.
Of course without integration the equations only gave the relation
without showing at all in what way the motion might depend upon it. It
seemed, however, to be certain, if the eddies were due to one particular
cause, that integration would show the birth of eddies to depend on some
definite value of D Um/n .'
 The story of his experiments using colour bands in glass tubes is well
known. His final apparatus, so effectively portrayed by the well known
illustration shown in Figure 9, consisted of a glass-sided tank, 6 feet
long, 18 inches deep and 18 inches wide. Inside it was a glass tube
with `a trumpet mouth of varnished wood, great care being taken to make
the surface of the wood continuous with that of the glass'. On the
right-hand side, the tube was connected to an iron pipe equipped with a
valve which could be controlled by means of a long lever. On the
left-hand side is the device for introducing a streak of dye into the
trumpet, while a float and dial wagister the waterer the water-level in
the tank and hence the volume being discharged through the glass tube.
The experiments, made in 1880, consisted of filling the tank with water,
allowing several hours for conditions to become steady, then opening the
valve, at first only slightly.
The story of his experiments using colour bands in glass tubes is well
known. His final apparatus, so effectively portrayed by the well known
illustration shown in Figure 9, consisted of a glass-sided tank, 6 feet
long, 18 inches deep and 18 inches wide. Inside it was a glass tube
with `a trumpet mouth of varnished wood, great care being taken to make
the surface of the wood continuous with that of the glass'. On the
right-hand side, the tube was connected to an iron pipe equipped with a
valve which could be controlled by means of a long lever. On the
left-hand side is the device for introducing a streak of dye into the
trumpet, while a float and dial wagister the waterer the water-level in
the tank and hence the volume being discharged through the glass tube.
The experiments, made in 1880, consisted of filling the tank with water,
allowing several hours for conditions to become steady, then opening the
valve, at first only slightly.
 Referring to Figure 10 the colour-band
established itself as a beautifully steady streak (10a) but a point was
reached on increasing the flow along the tube by opening the valve still
further, when `the colour band would all at once mix up with the
surrounding water, and fill the rest of the tube with a mass of coloured
water' (10b). `On viewing the tube by the light of an electric spark,
the mass of colour resolved itself into a mass of more or less distinct
curls, showing eddies.' (10c).
Referring to Figure 10 the colour-band
established itself as a beautifully steady streak (10a) but a point was
reached on increasing the flow along the tube by opening the valve still
further, when `the colour band would all at once mix up with the
surrounding water, and fill the rest of the tube with a mass of coloured
water' (10b). `On viewing the tube by the light of an electric spark,
the mass of colour resolved itself into a mass of more or less distinct
curls, showing eddies.' (10c).
 Reynolds proceeded to measure the critical velocity for onset of eddies
using three tubes of different diameter and in each case varying the
water temperature. To a first approximation, the Reynolds Numbers based
on these critical values of velocity were found to be the same (about
13000) for each of the tubes and for all water temperatures. He then
set out to find the critical condition for an eddying flow to change
into non-turbulent flow, referring to this as the `inferior limit'. To
do this, he allowed water to flow in a disturbed state from the mains
through a length of pipe and measured the pressure-drop over a five-foot
distance near the outlet (see Figure 11).
Reynolds proceeded to measure the critical velocity for onset of eddies
using three tubes of different diameter and in each case varying the
water temperature. To a first approximation, the Reynolds Numbers based
on these critical values of velocity were found to be the same (about
13000) for each of the tubes and for all water temperatures. He then
set out to find the critical condition for an eddying flow to change
into non-turbulent flow, referring to this as the `inferior limit'. To
do this, he allowed water to flow in a disturbed state from the mains
through a length of pipe and measured the pressure-drop over a five-foot
distance near the outlet (see Figure 11).
Starting with low flows and gradually increasing them, he found that at
a certain point the fluid levels in the differential manometer connected
to the pressure-holes began to fluctuate: this coincided with the change
in the character of the flow and provided visual evidence of the
attainment of the critical velocity which he later determined by
plotting the mean velocity against the pressure-gradient. Two sizes of
pipe were tested. The result was to demonstrate that the critical
velocities for the two pipes were in fact so related as to imply the
same critical value of the Reynolds Number (about 2000).
In this renowned contribution to the development of fluid mechanics,
Reynolds not only evolved the number to which his name was later
attached and determined the critical value below which flow in a pipe is
always stable and laminar, but also provided a detailed picture of the
resistance to flow in pipes. In addition, he took the further step of
showing that, for given conditions of surface roughness, the friction
coefficient is a unique function of the Reynolds Number. The following
year (1884) in his Presidential Address to the British Association in
Montreal, Lord Rayleigh paid this tribute:
... Professor Reynolds has traced with much success the passage from the
one state of things to the other, and has proved the applicability under
these complicated conditions of the general laws of dynamical similarity
as adapted to viscous fluids by Professor Stokes. In spite of the
difficulties which beset both the theoretical and experimental treatment,
we may hope to attain before long to a better understanding of a subject
which is certainly second to none in scientific as well as practical
interest.
Stokes himself, in his capacity as President of the Royal Society, also
singled out this exceptional paper in his statement of 30th November
1888 on the occasion of the presentation of a Royal Medal to Osborne
Reynolds `for his investigations in mathematical and experimental
physics, and on the application of scientific theory to engineering.'
In a subsequent shorter contribution entitled `On the two manners of
motion of water', Paper 48 (1883), Reynolds compared the characteristics
of flow in converging and diverging channels, pointing out that, whereas
in the former the conditions are favourable for producing steady flow,
in the latter the flow is likely to be turbulent and unsteady. This he
contrasted with flow in parallel channels where below a certain flow
rate steady streamline conditions prevail and above that turbulence is
encountered.
Back to Contents
Eleven years were to elapse before the major breakthrough in the
understanding of turbulent flows anticipated by Lord Rayleigh in his
Montreal address was made. It came with Reynolds' contribution `On the
Dynamical Theory of Incompressible Viscous Fluids and the Determination
of the Criterion' (Paper 62), the publication of which by the Royal
Society is celebrated in the centenary volume. This remarkable
development was of very great significance, dealing as it did with
matters which Reynolds considered:
`....must be of a general and important kind, such as the unexplained
laws of the resistance of fluid motions, the laws of universal
dissipation of energy and the second law of thermo-dynamics'
It was the culmination of twenty-five years of research and came as a
result of Reynolds conducting `a more rigorous examination and
definition of the geometrical basis on which the analytical method of
distinguishing between molar-motions and heat-motions in the kinetic
theory of matter is founded; and of the application of the same method
of analysis, thus definitely founded, to distinguish between the
mean-molar-motions and relative-molar-motions, where, as in the case of
steady-mean (turbulent) flow along a pipe, the more rigorous definition
of the geometrical basis shows the method to be strictly applicable.'
Its origins date back to Reynolds' interests in the properties of gases
at the outset of his career.
Section I of the paper is a lengthy introduction which sketches the
background to the work to be reported, states the objectives, outlines
the approach adopted and summarises the findings. He begins by tracing
the development between 1822 and 1845 of the equations governing fluid
motion, the Navier-Stokes equations. He refers to the comparisons
reported by Stokes in 1857 between theoretical solutions of the
equations and certain experimental observations, which seemingly proved
the assumptions made in the formulation of the equations. These were
restricted to the drag on slowly moving objects of small size and the
resistance to the flow of liquid at low rates through long tubes of
small bore. These he contrasts with examples where theoretical results
were found to be directly at variance with common experience in the case
of the motion of larger bodies at higher velocity and the discharge of
fluid through large tubes at greater flow rates. He points to the fact
that Stokes was aware that the discrepancies resulted from the presence
of eddies which rendered the actual motion other than that to which the
theoretical solutions referred.
Reynolds then goes on to discuss his own contribution in 1883 in
identifying the dimensionless parameter, the Reynolds Number, which
governs whether the flow in tubes will be direct (laminar) or unsteady
(turbulent), and establishing by experiment the value of `the inferior
limit', above which transition can occur. He asserts that:
`These experimental results completely removed the discrepancy
previously noticed, showing that whatever may be the cause, in those
cases in which the experimental results do not accord with those
obtained by the singular solution of the equations, the actual motions
of the water are different. But in this there is only a partial
explanation, for there remains the mechanical or physical significance
of the existence of the criterion to be explained'
Reynolds then flatly states `my object in this paper is to show that the
theoretical existence of an inferior limit to the criterion follows from
the equations of motion,' before continuing, `I also show that the limit
to the criterion obtained by this method of analysis, and by integrating
the equations of motion in space, appears as a geometrical limit to the
possible simultaneous distribution of certain quantities in space, and
in no wise depends on the physical significance of these quantities.'
Expressed in modern terms, Reynolds sought to write the components of
velocity in a turbulent flow in terms of mean and fluctuating quantities
and to perform averaging of the momentum equations. This showed that
these equations contained additional terms which could be thought of as
apparent stresses due to turbulence. He then derived equations for the
kinetic energy of the mean motion and the kinetic energy of the
turbulent motion and noticed that they contained terms, the turbulent
energy production terms, which represent the total exchange of energy
between the mean motion and the kinetic energy of the turbulence.
To explain the occurrence of transition in channel flows Reynolds
examined the conditions under which the turbulence energy could be
sustained. Using the turbulence energy equation and considering a
control volume for which the turbulent diffusion of turbulent energy
would integrate to zero, he arrived at a condition for `the inferior
limit' based on the idea that the total turbulence production must equal
the total turbulence dissipation. He analyzed the particular case of
flow between parallel walls driven by a pressure gradient. Using an
analytical function to describe a small disturbance superimposed on a
fully developed laminar flow he evaluated the total turbulence
production and the total turbulence dissipation. The result was that
they were in balance at a particular value of the Reynolds number of
517, based on the bulk mean velocity and the distance between the walls.
It is clear that Reynolds' historic paper contained the foundations of
modern turbulence modelling. The concept of turbulent stress, the role
of the turbulent production terms in the exchange of energy between the
mean motion and the turbulence and the dissipation of turbulence are
matters which remain of central importance in the subject of turbulence.
In essence he conceived the idea of the energy cascade in turbulent
flows. One can take his equations for the kinetic energy of the mean
motion and for turbulence energy and with little modification derive the
corresponding equations currently in use. A century later the basic
ideas contained in Reynolds' paper are still utilised in almost all our
numerical predictions of practical turbulent flows, at least in
situations close to industrial applications.
Back to Contents
We come next to a very different contribution, namely, Reynolds' theory
of hydrodynamic lubrication. The stimulus for this was the important
experimental research on `The Friction of Lubricated Journals' carried
out for the Institution of Mechanical Engineers by Beauchamp Tower,
first reported in 1883 and 1884.
This showed that it was possible for a journal to drag oil between
itself and the bearing, causing a rise of pressure sufficient to support
the shaft. Reynolds realized that the maintenance of a film of oil
between the shaft and its bearing might be explained by hydrodynamics on
the assumption that the centre of the rotating shaft shifted away from
the centre of the bearing in such a direction as to make the film of oil
thicker on the ingoing than on the outgoing side.
Excited by Tower's results and after a preliminary reference to them at
the 1884 British Association meeting, he pursued the subject with such
energy that his famous contribution `On the Theory of Lubrication...'
appeared in the Philosophical Transactions of the Royal Society in 1886
(Paper 52). In this very lengthy and detailed paper, Reynolds not only
formulated and integrated the hydrodynamic equations but also, by
allowing for the variation of viscosity with temperature, obtained close
agreement with the observed pressures.
The paper provides a very good example of Reynolds' approach of
discussing the physical or mechanical picture of things before
proceeding with the mathematics. Under the heading `General View of the
Action of Lubrication', he evolves the basic concepts involved by first
considering two plane surfaces. In Case 1 (Figure 12) they are parallel
to one another but AB is moving to the left with a velocity U and
`pumping' fluid between itself and the stationary surface CD. The
sloping lines show how the velocity varies between U at AB and zero at
CD. The pressure is constant between D and C although there are
tangential viscous stresses on the two surfaces.
 Next, he considers the same plates without tangential motion with the
upper one being forced downwards to squeeze out the fluid. A pressure
distribution is then created, reaching its highest value at the centre
(Case 2, Figure 12). He then combines the two: tangential motion and
squeezing of the surfaces together (Case 3, Figure 12). In this
instance, the distribution of pressure resembles that of Case 2, while
the mean viscous stress on CD is similar to that of Case 1.
Next, he considers the same plates without tangential motion with the
upper one being forced downwards to squeeze out the fluid. A pressure
distribution is then created, reaching its highest value at the centre
(Case 2, Figure 12). He then combines the two: tangential motion and
squeezing of the surfaces together (Case 3, Figure 12). In this
instance, the distribution of pressure resembles that of Case 2, while
the mean viscous stress on CD is similar to that of Case 1.
In order to account for the case of lubricated surfaces which are not
approaching one another, but which nevertheless are capable of
sustaining a transverse load, it only remains to visualise Case 4,
Figure 12, where one surface is inclined to the other. At the section
P1 Q1, there is the same uniform distribution of velocities as if the
surfaces were parallel to one another and at a distance P1Q1 apart. But
to either side of P1Q1, the velocities must be modified to preserve
continuity and so they adopt a shape similar to those of Case 3.
Correspondingly, the pressure follows the general shape of the curve
shown in Figure 12, with its maximum value at the section P1Q1. `This',
Reynolds concludes, `is the explanation of continuous lubrication. The
pressure of the intervening film of fluid would cause a force tending to
separate the surfaces.'
Ever practical, Reynolds then considers the question of a cylindrical
surface, developing the detailed mathematics and comparing the
implications with Tower's observations:
...The result of the whole research is to point to a conclusion
(important in Natural Philosophy) that not only in cases of intentional
lubrication, but wherever hard surfaces under pressure slide over each
other without abrasion, they are separated by a film of some foreign
matter, whether perceivable or not. And that the question as to whether
this action can be continuous or not, turns on whether the action tends
to preserve the matter between the surfaces at the points of pressure,
as in the apparently unique case of the revolving journal, or tends to
sweep it to one side, as is the result of all backwards and forwards
rubbing with continuous pressure...
An interesting postscript to this giant amongst Reynolds' papers is
provided by Paper 67 (1899), the final one which he read to the
Manchester Literary and Philosophical Society. This is entitled `On the
slipperiness of ice'. In it he proposes that an explanation of the
phenomenon is afforded by the ideas on lubrication contained in Paper 52.
Back to Contents
In 1893, we find Osborne Reynolds with an established reputation
presenting an interesting and authoritative discourse to the Royal
Institution (Paper 61) on an experimental technique which he had put to
very good use earlier, namely, `Study of fluid motion by means of
coloured bands'. In this he demonstrated many examples of the internal
motion of fluids. At the outset of the address he produced a box with a
hinged door on one side and a circular aperture on the one opposite.
This he used to project invisible vortex rings of air in the direction
of balloons suspended in the lecture theatre and exclaimed:
`Now I will ask you to look at these balloons. They are familiar
objects enough, and yet they are most sensitive anemometers, more
sensitive than anything else in this room; but even they do not show any
motion; each of them forms an internal bounding surface of the air. I
send an aerial messenger to them, and a small but energetic motion is
seen by which it acknowledges the message, and the same message travels
through the rest, as if a ghost touched them. It is a wave that moves
them. You do not feel it, and, but for the surfaces of the air formed
by the balloons, would have no notion of its existence.'
He then repeated the experiment but added smoke to the vortex-generating
box:
`I will now fulfil my promise to reveal the silent messenger I sent to
those balloons. The messenger appears in the form of a large smoke
ring, which is a vortex ring in air rendered visible by smoke instead of
colour ...
These are, if I may say so, the phenomenal instances of internal motion
of fluids. Phenomenal in their simplicity, they are of intense interest,
like the pendulum, as furnishing the clue to the more complex. It is by
the light we gather from their study that we can hope to interpret the
parallel of the vortex wrapped up in the wave, as applied to the wind of
heaven, and the grand phenomenon of the clouds, as well as those things
which directly concern us, such as the resistance of ships.'
Back to Contents
Paper 2 `The tails of comets, the solar corona, and the aurora, considered
as electrical phenomena'. Manchester Literary and Philosophical
Society, Memoirs, Series 3, Vol. 5, Session 1870-71.
Back
Paper 3A `On cometary phenomena'. Manchester Literary and Philosophical
Society, Memoirs, Series 3, Vol. 5, Session 1871-72.
Back
Paper 3B `On an electrical corona resembling the solar corona'. Manchester
Literary and Philosophical Society, Memoirs, Series 3, Vol. 5,
Session 1871-72. Back
Paper 4 `On the electro-dynamic effect which the induction of statical
electricity causes in a moving body. - This induction on the part
of the sun a probable cause of terrestrial magnetism'. Manchester
Literary and Philosophical Society, Memoirs, Series 3, Vol. 5,
Session 1871-72. Back
Paper 5 `On the electrical properties of clouds and the phenomena of
thunder storms'. Manchester Literary and Philosophical Society,
Proceedings, Vol. 12, Session 1872-73. Back
Paper 7 `On the bursting of trees and objects struck by lightning'.
Manchester Literary and Philosophical Society, Proceedings, Vol.
13, Session 1873-4.Back
Paper 7A `On the destruction of sound by fog and the inertness of a
heterogeneous fluid'. Manchester Literary and Philosophical
Society, Proceedings, Vol. 13, Session 1873-4.Back
Paper 11 `On the forces caused by evaporation from, and condensation at, a
surface'. Royal Society, Proceedings, No. 153, 1874.
Back
Paper 12 `On the surface-forces caused by the communication of heat'.
Philosophical Magazine, November 1874.Back
Paper 15 `On the action of rain to calm the sea'. Manchester Literary and
Philosophical Society, Proceedings, Vol. 14, Session 1874-5.
Back
Paper 16 `On the refraction of sound by the atmosphere'. Royal Society,
Proceedings, No. 155, 1874.Back
Paper 22 `On the refraction of sound by the atmosphere'. Royal Society,
Phil. Trans., Vol. 166, Pt. 1. Back
Paper 23 `On the forces caused by the communication of heat between a
surface and a gas; and on a new photometer'. Royal Society, Phil.
Trans., Vol. 166, Pt. 2.Back
Paper 27 `On the rate of progression of groups of waves and the rate at
which energy is transmitted by waves'. Nature, Vol. 16, Aug. 23,
1877.Back
Paper 29 `On the manner in which raindrops and hailstones are formed'.
Manchester Literary and Philosophical Society, Memoirs, Series 3,
Vol. 6, Session 1876- 77. Back
Paper 30 `On the formation of hailstones, raindrops, and snowflakes'.
Manchester Literary and Philosophical Society, Memoirs, Series 3,
Vol. 6, Session 1877- 78.Back
Paper 31 `On the internal cohesion of liquids and the suspension of a column
of mercury to a height more than double that of the barometer'.
Manchester Literary and Philosophical Society, Memoirs, Series 3,
Vol. 7, Session 1877-78. Back
Paper 33 `On certain dimensional properties of matter in the gaseous state'.
Royal Society, Phil. Trans., Pt. 2, 1879.Back
Paper 34 `Note on thermal transpiration'. (In a letter to Professor Stokes,
Sec. R.S. Communicated by Professor G.G. Stokes.) Royal Society,
Proceedings, No. 203, 1880.Back
Paper 35 `Some further experiments on the cohesion of water and mercury'.
Manchester Literary and Philosophical Society, Proceedings, Vol.
20, Session 1880-81.Back
Paper 38 `On the effect of oil in destroying waves on the surface of water'.
British Association Report, 1880.Back
Paper 39 `On surface-tension and capillary action'. British Association
Report, 1881. Back
Paper 40 `On the floating of drops on the surface of water depending only on
the purity of the surface'. Manchester Literary and Philosophical
Society, Proceedings, Vol. 21, Session 1881-82.
Back
Paper 44 `An experimental investigation of the circumstances which determine
whether the motion of water shall be direct or sinuous, and of the
law of resistance in parallel channels'. Royal Society, Phil.
Trans., 1883.Back
Paper 48 `On the two manners of motion of water'. Royal Institution,
Proceedings, March 1884. Back
Paper 50 `On the dilatancy of media composed of rigid particles in contact.
With experimental illustrations'. Philosophical Magazine,
December, 1885. Back
Paper 51 `Experiments showing dilatancy, a property of granular material,
possibly connected with gravitation'. Royal Institution,
Proceedings, February 12, 1886. Back
Paper 52 `On the theory of lubrication and its application to Mr. Beauchamp
Tower's experiments, including an experimental determination of
the viscosity of olive oil'. Royal Society, Phil. Trans., Pt. 1,
1886.Back
Paper 61 `Study of fluid motion by means of coloured bands'. Royal
Institution, Proceedings, June 2, 1893. Back
Paper 62 `On the dynamical theory of incompressible viscous fluids and the
determination of the criterion'. Royal Society, Phil. Trans.,
1895.Back
Paper 67 `On the slipperiness of ice'. Manchester Literary and
Philosophical Society, Memoirs and Proceedings, Vol. 43, Session
1898-9.Back
Document written by
Prof. J.D. Jackson
Centre for the History of Science, Technology & Medicine
Faculty of Life Sciences
University of Manchester, Manchester M13 9PL
e-mail: jdjackson@manchester.ac.uk
Web Pages prepared by Dr. J. E. Byrne
Back to Contents ||
Back to Main Document ||
Reynolds the Engineer ||
 In a presentation to the Manchester Literary and Philosophical Society,
`On the action of rain to calm the sea' (Paper 15, 1875) Reynolds showed
by experiment that vortex rings produced by droplets of rain cause water
to be carried well below the surface in appreciable amounts leading to
the damping of wave motion (see Figure 2).
In a presentation to the Manchester Literary and Philosophical Society,
`On the action of rain to calm the sea' (Paper 15, 1875) Reynolds showed
by experiment that vortex rings produced by droplets of rain cause water
to be carried well below the surface in appreciable amounts leading to
the damping of wave motion (see Figure 2).
 The earliest of these,
Papers 2, 3A and 3B (1870-1872), are all closely
related. In Papers 2 and 3A the tails of comets, the solar corona and
the aurora are considered as electrical phenomena. In Paper 3B (1872),
a corona resembling the solar corona produced by discharging electricity
from a brass ball in a partially evacuated receiver is described (see
Figure 1). In Paper 4 (1872), the induction of static electricity on the
part of the sun is proposed as a probable cause of terrestrial magnetism
and in Paper 5 (1872) the inductive action of the sun on the electrical
properties of clouds is considered with respect to thunderstorms.
Paper 7 (1873) `On the bursting of trees and other objects struck by lightning'
reports an experiment showing that the explosive effect of a lightning
strike is due to the rapid evaporation of moisture into steam.
The earliest of these,
Papers 2, 3A and 3B (1870-1872), are all closely
related. In Papers 2 and 3A the tails of comets, the solar corona and
the aurora are considered as electrical phenomena. In Paper 3B (1872),
a corona resembling the solar corona produced by discharging electricity
from a brass ball in a partially evacuated receiver is described (see
Figure 1). In Paper 4 (1872), the induction of static electricity on the
part of the sun is proposed as a probable cause of terrestrial magnetism
and in Paper 5 (1872) the inductive action of the sun on the electrical
properties of clouds is considered with respect to thunderstorms.
Paper 7 (1873) `On the bursting of trees and other objects struck by lightning'
reports an experiment showing that the explosive effect of a lightning
strike is due to the rapid evaporation of moisture into steam.
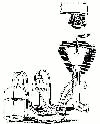

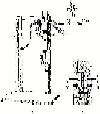

 Reynolds' interest in the physics of fluids extended to liquids. In
Papers 31 (1877) and 35 (1880) delivered to the Manchester Literary and
Philosophical Society he reported experiments on the internal cohesion
of mercury and water. By careful exclusion of air he was able to
suspend a column of mercury to a height of more than double that of the
barometer (see Figure 7).
Reynolds' interest in the physics of fluids extended to liquids. In
Papers 31 (1877) and 35 (1880) delivered to the Manchester Literary and
Philosophical Society he reported experiments on the internal cohesion
of mercury and water. By careful exclusion of air he was able to
suspend a column of mercury to a height of more than double that of the
barometer (see Figure 7).




