Bifurcations with dihedral symmetry

Any function invariant under the D_n action on the plane is a function of the two fundamental homogeneous polynomials:
$$N=x^2+y^2 = |z|^2,\quad \mbox{and} \quad P = \mathrm{Re}(z^n)$$ The following diagrams show level sets of the functions $$h_\lambda(z) = \lambda N +aN^2 + bP.$$ So $h_\lambda$ has a local min at the origin when $\lambda\gt0$.

We need to assume $b\neq0$, otherwise the function $h_0$ does not have an isolated singularity.
And w.l.o.g, we can assume $b>0$ (after a possible rotation in the plane).
(If $b=0$ we would need to take into account higher order terms such as $P^2$).
Mostly we take $a=b=1$, but for $n=4$ we must take $a\ne\pm b$.

In the diagrams, if points $p$ and $q$ are such that $p$ is coloured bluer than $q$, then $h(p) \lt h(q)$.
D_n	λ<0	λ>0	discussion
n=3		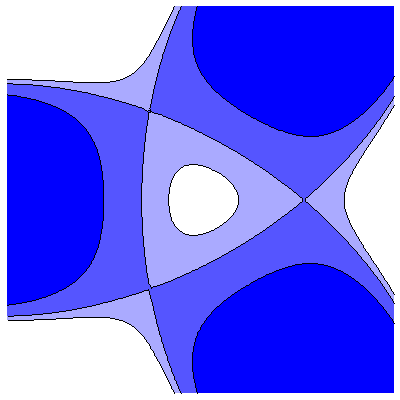	On both sides of the bifurcation, there are 3 saddle points; this is a traditional transcritical bifurcation
n=4 (i)			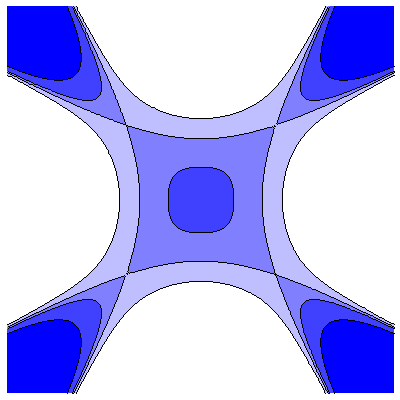(a<b) On both sides of the bifurcation, there are 4 saddle points; this is a traditional transcritical bifurcation
n=4 (ii)		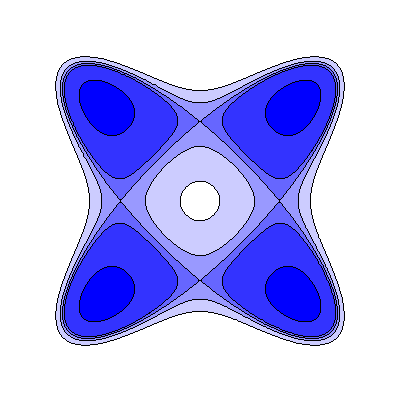	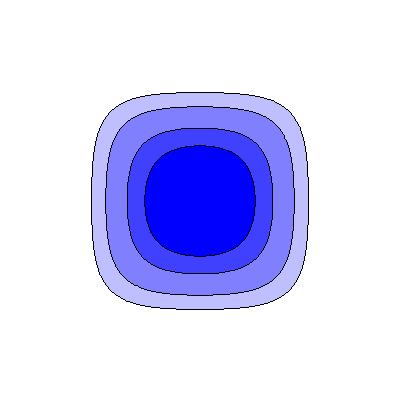(a>b) On one side there are 4 saddles and 4 local minima, and on the other no bifurcating critical points
n=5			On one side there are 5 saddles and 5 local minima, and on the other no bifurcating critical points
n=6		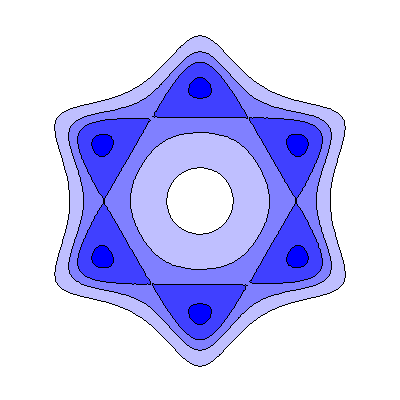	On one side there are 6 saddles and 6 local minima, and on the other no bifurcating critical points

Remark: Notice how $n = 3$ and $n = 4(i)$ are similar, while $n = 4(ii)$ and $n \gt 4$ are similar.
The general pattern depends on which of the terms $aN^2$ or $bP$ dominates.
Notice that all the bifurcating critical points lie in lines of symmetry;
this means that the solutions they represent in a given problem will have an order 2 symmetry.

James Montaldi
home page