MASIE Home Page

About this document

MASIE
Mechanics and Symmetry in Europe

Bibliography

AHMR

Abarbanel, H.D.I., D.D. Holm, J.E Marsden, and T.S. Ratiu [1986] Nonlinear stability of stratified fluid equilibria, Phil. Trans. Roy. Soc. London A 318, 349-409.

AM78

Abraham, R., and Marsden, J.E. [1978] Foundations of Mechanics. Second edition, Addison-Wesley.

AS81

Abud, M., and Sartori, G. [1981] The geometry of orbit-space and natural minima of Higgs potentials. Physics Letters 104B(2):147-152.

AS83

Abud, M., and Sartori, G. [1983] The geometry of spontaneous symmetry breaking. Annals of Physics 150, 307-372.

AA93

Akhmediev, N. and Ankiewicz, A. [1993] Solitons, nonlinear pulses and beams Chapman & Hall.

ACG91

Arms, J.M., Cushman, R., and Gotay, M.J. [1991] A universal reduction procedure for Hamiltonian group actions. In The Geometry of Hamiltonian Systems. T.S. Ratiu ed. pages 33-51. Springer Verlag.

AGJ90

Arms, J.M., Gotay, M., and Jennings, G.[1990] Geometric and algebraic reduction for singular momentum maps. Adv. in Math. 79, 43-103.

AMM81

Arms, J.M., Marsden, J.E., and Moncrief, V.[1975] Symmetry and bifurcations of momentum mappings. Comm. Math. Phys. 78, 455-478.

A66

Arnold, V.I. [1969] Sur la géométrie differentielle des groupes de Lie de dimension infinie et ses aplications à l'hydrodynamique des fluids parfaits, Ann. Inst. Fourier, Grenoble 16, 319-361.

A65

Arnold, V.I. [1965] Conditions for nonlinear stability of the stationary plane curvilinear flows of an ideal fluid, Dokl. Mat. Nauk 162, 773-777.

A69

Arnold, V.I. [1969] An a priori estimate in the theory of hydrodynamics stability, [English translation] Amer. Math. Soc. Transl. 19, 267-269.

AK98

Arnold, V.I., and Khesin, B. [1998] Topological Methods in Hydrodynamics. Springer Verlag.

BC98

Barenblatt, G.I. and Chorin, A.J. [1998] New perspectives in turbulence: scaling laws, asymptotics, and intermittency, SIAM Rev. 40, 265-291.

B91

Bates,L. [1991] Monodromy in the champagne bottle. Journal of Applied Mathematics and Physics ZAMP 42, 837-847.

BL97

Bates, L. and Lerman, E. [1997] Proper group actions and symplectic stratified spaces. Pacific J. Math. 181(2):201-229.

BZ93

Bates, L. and Zou, M. [1993] Degeneration of Hamiltonian monodromy cycles. Nonlinearity 6, 313-335.

BF??

Benettin and Fasso, F., (Nekhoroshev stability of equilibria)

BG94

Benettin, G. and Giorgilli, A. [1994] On the Hamiltonian interpolation of near to the identity symplectic mappings with application to symplectic integration algorithms, J. Stat. Phys. 74, 1117-1143.

B72

Benjamin, B. [1972] The stability of solitary waves, Proc. Royal Soc. London, A 328, 153-183.

BKMR94

Bloch, A.M., P.S. Krishnaprasad, J.E. Marsden and T.S. Ratiu [1994] Dissipation induced instabilities, Ann. Inst. H. Poincaré, Analyse Nonlinéaire 11, 37-90.

BKMR

Bloch, A.M., P.S. Krishnaprasad, J. Marsden, and T.S. Ratiu [1996] The Euler-Poincaré equations and double bracket dissipation, Comm. Math. Phys. 175, 1-42.

Born98

Bornemann, F.A. [1998] Homogenization in time of singularly perturbed conservative mechanical systems. Lecture Notes in Mathematics 1687, Springer-Verlag.

Bri90

Bridges, T. J. [1990] Bifurcation of periodic solutions near a collision of eigenvalues of opposite signature. Math. Proc. Camb. Phil. Soc. 108, 575-601.

Bri97

Bridges, T.J. [1997] Multi-symplectic structures and wave propagation, Math. Proc. Camb. Phil. Soc. 121, 147-190.

Bri98

Bridges, T.J. [1998] Toral-equivariant partial differential equations and quasiperiodic patterns, Nonlinearity 11, 467-500.

BD99

Bridges, T.J. and G. Derks [1999] Unstable eigenvalues and the linearisation about solitary waves and fronts with symmetry, Proc. Roy. Soc. Lond. A, to appear.

BR99

Bridges, T.J. and Reich, S. [1999] Multi-symplectic integrators: numerical schemes for Hamiltonian PDEs that conserve symplecticity, UniS preprint.

BZ95a

Brodersen S. and Zhilinskii B. [1995] Transfer of clusters between the vibrational components of CF₄. J. Mol. Spectrosc. 169:1-17.

BZ95b

Brodersen S. and Zhilinskii B. [1995] The rotational structure of the vibrational states and substates of symmetry E in CF₄. J. Mol. Spectrosc. 172:303-318.

BC97

Budd, C.J. and Collins, G.J. [1997], Symmetry based numerical methods for partial differential equations, Proc. 1997 Dundee Conference in Numerical Analysis.

CRS99

CastrillĪn-Lopez, M., T.S. Ratiu, and S. Shkoller [1999] Reduction in principal fiber bundles: covariant Euler-Poincaré equations, Proc. Amer. Math. Soc., to appear.

CHMR98

Cendra, H., D.D. Holm, J.E. Marsden, and T.S. Ratiu [1998] Lagrangian reduction, the Euler-Poincaré equations, and semidirect products, Amer. Math. Soc. Transl. 186, 1-25.

Ch69

Chandrasekhar, S. [1969] Ellipsoidal Figures of Equilibrium. Dover Publications, Inc.

Cd98

Child, M.S. [1998], Quantum states in a Champagne bottle, J. Phys. A. 31, 657--670.

CWT99

Child, M.S., Weston, T. and Tennyson, J. [1999], Quantum monodromy in the spectrum of H₂O and other systems, (to appear).

C86

Chossat, P. [1986] Bifurcation secondaire de solutions quasi-périodiques dans un problème de bifurcation invariant par symétrie O(2), C. R. Acad. Sci. Paris Sér. I Math. 302, 539-541.

CI85

Chossat, P. and Iooss, G. [1985] Primary and secondary bifurcations in the Couette-Taylor problem, Japan J. Appl. Math 2, 37-68.

CL99

Chossat, P. and Lauterbach, R. [1999] Methods in equivariant bifurcation and dynamical systems and their applications. To appear in Nonlinear Studies Series, World Scientific, Singapore.

Cu83

Cushman, R.H. [1983] Geometry of the energy momentum mapping of the spherical pendulum. C.W.I. Newsletter 1:4-18.

CB95

Cushman, R.H. and Bates, L.M. [1995] The magnetic spherical pendulum. Meccanica, 30:271-289.

CB97

Cushman, R.H., and Bates, L.M. [1997] Global Aspects of Classical Integrable Systems. Birkhäuser Verlag.

CD88

Cushman, R.H. and Duistermaat, J.J. [1988] The quantum mechanical spherical pendulum, Bull. Am. Math. Soc. 19:475.

CD99

Cushman, R.H. and Duistermaat, J.J. [1999] Nonhamiltonian monodromy. Preprint, University of Utrecht.

CK85

Cushman, R.H. and Knörrer, H. [1985] The energy momentum mapping of the Lagrange top. pp. 12-24 in: Differential Geometric methods in Mathematical Physics (Proceedings, Clausthal, 1983). Eds.: H.D. Doebner and D.J. Hennig. Lecture Notes in Mathematics 1139, Springer-Verlag, Berlin.

CM90

Cushman, R.H. and van der Meer, J.C. [1990] The Hamiltonian Hopf bifurcation in the Lagrange top. pp. 26-38 in: Géométrie Symplectique et Mécanique (Proceedings, La Grande Motte, 1988). Ed.: C. Albert, Lecture Notes in Mathematics 1416, Springer-Verlag, Berlin.

CS99

Cushman, R.H. and Sadovskii, D. [1999] Monodromy in perturbed Kepler systems: hydrogen atom in crossed fields. Europhys. Lett in press.

DZKS90

Davarashvili O.I., Zhilinskii B. I., Krivtsun V.M., Sadovskii D.A., and Snegirev E.P. [1990] Experimental study of a sequence of quantum bifurcations. JETP Lett.(USA) 51:18-21.

DMM92

Dellnitz, M., Melbourne, I., and Marsden, J. E. [1992] Generic Bifurcation of Hamiltonian vector fields with symmetry. Nonlinearity 5:979-996.

DR98

Derks, G. and T.S. Ratiu [1998] Attracting curves in Navier-Stokes and reduced magnetohydrodynamics, The Royal Society. Proceedings: Math., Phys. and Eng. Sci., Series A 454, 1407-1444.

DLR95

Derks, G., D.K. Lewis, and T.S. Ratiu [1995] Approximations with curves of relative equilibria in Hamiltonian systems with dissipation. Nonlinearity 8, 1087-1113.

DHLMRS99

Deuflhard, P., Hermans, J., Leimkuhler, B., Mark, A.E., Reich, S. and Skeel, R.D. (Eds.) [1999] Computational Molecular Dynamics: Challenges, Methods, Ideas, Lecture Notes in Computational Science and Engineering 4, Springer-Verlag.

D80

Duistermaat, J.J. [1980] On global action-angle coordinates. Comm. Pure Appl. Math. 33:687-706.

D97

Duistermaat, J.J. [1997] The monodromy in the Hamiltonian Hopf bifurcation. Journal of Applied Mathematics and Physics ZAMP 48:1-6.

EM70

Ebin , Marsden, J.E. [1970], Groups of diffeomorphisms and the motion of an incompressible fluid, Ann. Math. 92, 102-163.

F??

Fasso, (Nekhoroshev estimates for Riemann ellipsoids)

FR98

FassŽ, F. and T.S. Ratiu [1998] Compatibility of symplectic structures adapted to noncommutatively integrable systems, J. Geom. and Physics 27, 199-220.

Ro95

Robinson, C. [1995] Dynamical Systems. CRC Press, Inc.

FSSW96

Fiedler, B., Sandstede, B., Scheel, A. and Wulff, C. [1996] Bifurcation from relative equilibria of noncompact group actions: skew products, meanders and drifts. Doc. Math. J. DMV 1:479-505.

Fi80

Field, M. J. [1980] Equivariant dynamical systems. Trans. Amer. Math. Soc., 259(1):185-205.

Fi91

Field, M. J. [1991] Local structure of equivariant dynamics. In Singularity Theory and its Applications. M. Roberts and I. Stewart eds. Lecture Notes in Mathematics, 1463. Springer-Verlag.

GSS99

García-Archilla, B., Sanz-Serna, J.M. and Skeel, R.D. [1999] Long-Time-Step Methods for Oscillatory Differential Equations, SIAM J. Sci. Comput., to appear.

GKM96

Z. Ge, H.-P. Kruse, and J. Marsden[1996] The limits of Hamiltonian structures in three-dimensional elasticity, shells and rods, J. Nonlin. Science, 6, 277-302.

GKMS95

Z. Ge, H.-P. Kruse, J. Marsden, and C, Scovel[1995] The Hamiltonian structures in the shallow water approximations, Canadian Appl. Math. Quaterly, 3(3), 1-116.

GM88

Ge, Z. and Marsden, J.E. [1988] Lie-Poisson Hamilton-Jacobi Theory and Lie-Poisson Integrators, Physics Letters A 133, 134-139.

GMSD95

Golubitsky, M., Marsden, J.E., Stewart, I., and Dellnitz, M. [1995] The constrained Liapunov-Schmidt procedure and periodic orbits. In Normal Forms and Homoclinic Chaos, pages 81-127. Langford, W. F. and Nagata, W. eds. Fields Institute Communications, 4.

GoS85

Golubitsky, M., and Schaeffer, D.G. [1985] Singularities and Groups in Bifurcation Theory: Vol. I. Applied Mathematical Sciences, Vol. 51, Springer-Verlag.

GoS85

Golubitsky, M. and Stewart, I. [1985] Hopf bifurcation in the presence of symmetry. Arch. Rational Mech. Anal., 87:107-165.

GoS87

Golubitsky, M. and Stewart, I. With an appendix by J. E. Marsden. [1987] Generic bifurcation of Hamiltonian systems with symmetry. Physica D, 24:391-405.

GSS85

Golubitsky, M., Stewart, I., and Schaeffer, D.G. [1985] Singularities and Groups in Bifurcation Theory: Vol. II. Applied Mathematical Sciences, Vol. 69, Springer-Verlag.

GS84a

Guillemin, V. and Sternberg, S. [1984] A normal form for the moment map. In Differential Geometric Methods in Mathematical Physics. S. Sternberg ed. Mathematical Physics Studies, 6. D. Reidel Publishing Company.

GS84b

Guillemin, V. and Sternberg, S. [1984] Symplectic Techniques in Physics. Cambridge University Press.

HP77

Harter, W. G., and C. W. Patterson. [1977] Orbital level splitting in octahedral symmetry and SF₆ rotational spectra. I. Qualitative features of high J levels. J. Chem. Phys. 66, 4872-4885.

H88

Harter, W. G. [1988] Computer graphical and semiclassical approaches to molecular rotations and vibrations. Comp. Phys. Rep. 8, 319-394.

HP84

Harter, W.G. and Patterson, C.W. [1984] Rotational energy surfaces and high-J eigenvalue structure of polyatomic molecules. J. Chem. Phys. 80, 4241-4261.

HL99

Hochbruck, M. and Lubich, Ch. [1999] A bunch of time integrators for quantum/classical molecular dynamics, in: Computational Molecular Dynamics: Challenges, Methods, Ideas, P. Deuflhard et al. (eds), Lecture Notes in Computational Science and Engineering Vol. 4, Springer-Verlag, pp. 421-432.

HMRW85

Holm, D.D., J.E. Marsden, .S. Ratiu, and A. Weinstein [1985] Nonlinear stability of fluid and plasma equilibria, Physics Reports 123, 1-116.

HMR86

Holm, D.D., J.E. Marsden, and T.S. Ratiu [1986] Nonlinear stability of the Kelvin-Stuart cat's eyes flow, in Nonlinear Systems of PDEs in Applied Mathematics(B. Nicolaenko, ed.), Lectures in Applied Mathematics, 23, 171-186.

HMR98

Holm, D. D., J. E. Marsden and T. S. Ratiu [1998] Euler-Poincaré models of ideal fluids with nonlinear dispersion, Phys. Rev. Lett. 349, 4173-4177.

HMR98a

Holm, D.D., J.E. Marsden, and T.S. Ratiu [1998] The Euler-Poincaré equations and semidirect products with applications to continuum theories, Advances in Math., 137, 1-81.

HMR99

Holm, D.D., J.E. Marsden, and T.S. Ratiu [1999] Euler-Poincaré equations in geophysical fluid dynamics, Proceedings of the Isaac Newton Institute, to appear.

HLR99a

Hoveijn, I., Lamb, J.S.W. and Roberts, R.M. [1999] Normal forms and unfoldings of time-reversible equivariant linear systems. In preparation.

HLR99b

Hoveijn, I., Lamb, J.S.W. and Roberts, R.M. [1999] Time-reversible equivariant linear Hamiltonian systems. In preparation.

HL97

Huang, W. and Leimkuhler, B. [1997] The Adaptive Verlet Method, SIAM J. Sci. Comput. 18, 239-256.

HRR94

Huang, W, Ren Y. and Russell, R.D. [1994] Moving mesh methods based on moving mesh partial differential equations, J. Comput. Phys. 112, 279-290.

IRS99

Izaguirre, J.A., Reich, S. and Skeel, R.D. [1999] Longer time steps for molecular dynamics, J. Chem. Phys., to appear.

K67

Kato, Y. [1967] On classical solutions of the two-dimensional non-stationary Euler equations, Arch. Rat. Mech. Anal. 24 (3), 302-324.

KP96

Kozin, I.N. and Pavlichenkov, I.M. [1996] Bifurcation in rotational spectra of nonlinear AB₂ molecules. J. Chem. Phys. 104:4105-4113.

KRT99a

Kozin, I.N, Roberts, R.M. and Tennyson, J. [1999] Symmetry and structure of rotating H₃⁺. To appear in J. Chem. Phys..

KRT99b

Kozin, I.N, Roberts, R.M. and Tennyson, J. [1999] Relative equilibria of H₂D⁺ and D₂H⁺. In preparation.

KRSZ

Krivtsun V.M., Sadovskii D.A., and Zhilinskii B. I. [1990] Critical phenomena and diabolic points in rovibrational energy spectra of spherical top molecules. J.Mol.Spectrosc. 139:126-146.

KSSSZ

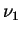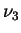Krivtsun V.M., Sadovskii D.A., Snegirev E.P., Shotov A.P., and Zasavitskií I.I. [1990] Diode Laser Study of the $\nu_1$ and $\nu_3$ Bands of the ¹²⁰SnH₄ Molecule. J. Mol. Spectrosc. 139:107-125.

Kr90

Krupa, M. [1990] Bifurcations of relative equilibria. SIAM J. Math. Anal. 21(6):1453-1486.

Kr99a

H.-P. Kruse [1999] On the configuration manifold of a liquid bridges, J. Geometry and Physics, 29, 260-282.

Kr99b

H.-P. Kruse [to appear] Bifurcation of rotating inviscid liquid bridges with fixed contact angles, Proc. London Math. Soc..

Kr99c

H.-P. Kruse [to appear] Bifurcation of rotating inviscid liquid bridges with fixed contact lines, ZAMM.

KMM99

H.-P. Kruse, A. Mahalov, and J. Marsden [1999] On the Hamiltonian structure and three-dimensional instabilities of rotating liquid bridges, Fluid Dynamics Research 24, 37-59.

KS98

H.-P. Kruse, and J. Scheurle 1998] On the bifurcation stability of rigidly rotating inviscid liquid bridges, J. Nonl. Science, 8, 215-232.

Ku98

Kudryavtseva, E. A. [1998] Generalization of geometric Poincaré theorem for small perturbations. Regular and chaotic dynamics, 3(2):46-65.

LaM99

Lamb, J.S.W. and Melbourne, I.[1999] Bifurcation from discrete rotating waves. To appear in Arch. Rat. Mech. Anal.

LaR99

Lamb, J.S.W. and Roberts, R.M. [1999] Reversible equivariant linear systems. To appear in J. Diff. Eq..

LS98

Lerman, E. and Singer, S.F. [1998] Relative equilibria at singular points of the momentum map. Nonlinearity 11 1637-1649.

LT99

Lerman, E. and Tokieda, T. F. [1999] On relative normal modes. C. R. Acad. Sci. Paris Sér. I Math., 328:413-418.

L9???

Lewis, D. [199?] Lagrangian block diagonialization

Lew93

Lewis, D. [1993] Bifurcation of liquid drops. Nonlinearity 6 491-522.

LMR87

Lewis, D.K., J.E. Marsden, and T.S. Ratiu [1987] Stability and bifurcation of a rotating planar liquid drop, Journal of Math. Phys., 28, 2508-2515.

LR96

Lewis, D.K. and T.S. Ratiu [1996] Rotating n-gon/kn-gon vortex configurations, Journ. Nonlinear Science 6, 385-414.

LRSM92

Lewis, D.K., T.S. Ratiu, J.C. Simo, and J.E. Marsden [1992] The heavy top: a geometric treatment, Nonlinearity, 5, 1-48.

LeR99

Lewis, A.D. and Roberts, R.M. [1999] Mechanical systems on homogeneous spaces. In preparation.

LP98

Li, Y.A. and Promislow, K. [1998] Structural stability of non-ground state traveling waves of coupled nonlinear Schrödinger equations, Physica D, 124:137-165.

LM87

Libermann, P., and Marle, C.-M. [1987] Symplectic Geometry and Analytical Mechanics. Reidel.

Liv95

Liverani, G. [1995] Decay of correlation, Ann. of Math. 142, 239-301.

LK95

Lu, Z. and Kellman, M.E. [1995] ?? Chem. Phys. Lett. 247:195-??.

M98

Makarewicz, J. [1998] ?? J. Chem. Phys 108:469-??.

Mar85

Marle, C.-M. [1985] Modéle d'action hamiltonienne d'un groupe the Lie sur une variété symplectique. Rend. Sem. Mat. Univers. Politecn. Torino, 43(2):227-251.

Mar92

Marsden, J.E. [1992] Lectures on Mechanics. London Mathematical Society Lecture Note Series, volume 174. Cambridge University Press.

MMPR98

Marsden,. J.E., G. Misiolek, M. Perlmutter, and T.S. Ratiu [1998] Symplectic reduction for semidirect products and central extensions, Diff. Geom. and its Appl., 9, 173-212.

MPS99

Marsden, J.E., Patrick, G.P. and Shkoller, S. [1999] Multisymplectic geometry, variational integrators, and nonlinear PDEs, Comm. in Math. Phys. 199 351-395.

MRS99

Marsden, J.E., T.S. Ratiu, and S. Shkoller [1999] The geometry and analysis of the averaged Euler equations with normal boundary conditions, Geom.and Funct. Anal., to appear

MR86

Marsden, J.E., and Ratiu, T.S. [1986] Reduction of Poisson manifolds. Letters in Mathematical Physics, 11:161-169.

MR94

Marsden, J.E. and Ratiu, T.S. [1999] Introduction to Mechanics and Symmetry, Second edition,. Texts in Applied Mathematics, volume 17. Springer-Verlag.

MS93

Marsden, J.E., and Scheurle, J. [1993] Lagrangian reduction and the double spherical pendulum. Z. Angew. Math. Phys., 44:17-43.

MW74

Marsden, J.E., and Weinstein, A. [1974] Reduction of symplectic manifolds with symmetry. Rep. Math. Phys., 5(1):121-130.

MR89

Mazer, A. and T.S. Ratiu [1989] Hamiltonian formulation of adiabatic free boundary Euler flows, Journal of Geometry and Physics, 6, 271-291.

MR89a

Mazer, A. and T.S. Ratiu [1989] Formal stability in two-dimensional self-gravitating Euler fluids, in The Connection between Infinite Dimensional and Finite Dimensional Dynamical Systems (B. Nicolaenko, C. Foias, R. Teman, eds.) Cont. Math., 99, 233-258.

McLS95

McLachlan, R.I., Scovel, C. [1995] Equivariant Constrained Symplectic Integration, J. Nonlinear Science 5, 233-256.

McL94

McLachlan, R.I. [1994] Symplectic integration of Hamiltonian wave equations, Numer. Math. 66, 465-492.

vdM85

van der Meer, J. C. [1985] The Hamiltonian Hopf Bifurcation. Lecture Notes in Mathematics, 1160. Springer Verlag.

vdM90

van der Meer, J. C. [1990] Hamiltonian Hopf bifurcation with symmetry. Nonlinearity 3, 1041-1056.

vdM96

van der Meer, J. C. [1996] Degenerate Hamiltonian Hopf bifurcations. In Conservative Systems and Quantum Chaos, pages 159-176. Bates, L. M. and Rod, D. L., eds. Fields Institute Communications 8.

MD93

Melbourne, I., and Dellnitz, M. [1993] Normal forms for linear Hamiltonian vector fields commuting with the action of a compact Lie group. Math. Proc. Camb. Phil. Soc. 114, 235-268.

Men87

Menyukm C. [1987] Stability of solitons in birefringent optical fibres, I. Equal propagation amplitudes, Opt. Lett. 12, 614-616.

Mey73

Meyer, K. R. [1973] Symmetries and integrals in mechanics. In Dynamical Systems, pp. 259-273. M.M. Peixoto, ed. Academic Press.

Mey86

Meyer, K. R. [1986] Bibliographical notes on generic bifurcation in Hamiltonian systems. In Multiparameter Bifurcation Theory, Contemp. Math. no. 56 (American Mathematical Society), pp. 373-381.

MeyS71

Meyer, K. R. and Schmidt, D. S. [1971] Periodic orbits near L₄ for mass ratios near the critical mass ratio of Routh. Celestial Mech., 99-109.

MZ97

Michel L. and Zhilinskii B. [1997] Rydberg states of atoms and molecules. Group theoretical and topological analysis. 76 p. Preprint IHES/P/97/54.

MR98

Michor, P. and T.S. Ratiu [1998] On the geometry of the Bott-Virasoro group, Journal of Lie Theory 8, 293-309.

M97a

Montaldi, J.A. [1997] Persistence and stability of relative equilibria. Nonlinearity 10, 449-466.

M97b

Montaldi, J.A. [1997] Persistance d'orbites périodiques relatives dans les systèmes hamiltoniens symétriques. C.R.Acad. Sci. Paris Série I 324, 553-558.

MR99a

Montaldi, J.A., and Roberts, R.M. [1999] Relative equilibria of molecules. J. Nonlinear Sc. 9, 53-88.

MR99b

Montaldi, J.A., and Roberts, R.M. [1999] Semisymplectic group actions and time-reversing symmetries of relative equilibria. In preparation.

MRS88

Montaldi, J.A., Roberts, R.M., and Stewart, I.N. [1988] Periodic solutions near equilibria of symmetric Hamiltonian systems. Phil. Trans. Roy. Soc. Lond. A 325, 237-293.

M76

Moser, J. [1976] Periodic orbits near an equilibrium and a theorem by Alan Weinstein. Comm. Pure Appl. Math. 29, 727-747.

MK91

Muraki, D.J. and Kath, W.L. [1991] Hamiltonian dynamics of solitons in optical fibres. Physica D 48 53-64.

Or98

Ortega, J.-P. [1998] Symmetry, Reduction, and Stability in Hamiltonian Systems. Ph.D. Thesis. University of California, Santa Cruz. June, 1998.

OR97

Ortega, J.-P. and Ratiu, T.S. [1997] Persistence and smoothness of critical relative elements in Hamiltonian systems with symmetry. C.R. Acad. Sci., Paris, Série I 325, 1107-1111.

OR98a

Ortega, J.-P. and Ratiu, T.S. [1998] Singular reduction of Poisson manifolds. Letters in Mathematical Physics 46, 359-372.

OR99a

Ortega, J.-P. and Ratiu, T.S. [1998] Stability of Hamiltonian relative equilibria. Nonlinearity 12, 693-720.

OR99b

Ortega, J.-P. and Ratiu, T. S. [1999] Lectures on Hamiltonian singular reduction. Preprint.

PF90

Paré, M. and Florjanczyk, M. [1990] Approximate model of soliton dynamics in all-optical couplers, Phys. Rev. A 41:6287-6295.

P95

Patrick, G.W. [1995] Relative equilibria of Hamiltonian systems with symmetry: linearization, smoothness and drift. J. Nonlin. Sc. 5, 373-418.

P98

Patrick, G.W. [1998] Dynamics near relative equilibria: nongeneric momenta at a 1:1 group reduced resonance. Preprint.

PR99

Patrick, G.W. and Roberts, R.M. [1999] The transversal relative equilibria of a Hamiltonian system with symmetry. Preprint.

PH77

Patterson, C. W., and W.G.Harter. [1977] Orbital level splitting in octahedral symmetry and SF₆ rotational spectra. II. Quantitative features of high J levels. J.Chem. Phys. 66, 4886-4892.

P93

Pavlichenkov I.M. [1993] Bifurcations in quantum rotational spectra. Phys. Rep. 226:17-279.

PZ85

Pavlichenkov I.M., and Zhilinskií B.I. [1985] Rotation of molecules around specific axes: axes reorientation under rotational excitation. Chem. Phys. 100, 339-354.

PZ88

Pavlichenkov, I.M. and Zhilinskií, B.I. [1988] Critical phenomena in rotational spectra. Ann. Phys. 184 1-32.

PVZ88a

Pavlov-Verevkin V.B. and Zhilinskií, B.I. [1988] Rearrangements of the vibrational polyadic spectra with excitation: two-mode case. Chem. Phys. 128 429-437.

PVZ88b

Pavlov-Verevkin V.B. and Zhilinskií, B.I. [1988] Effective Hamiltonians for vibrational polyads: Integrity basis approach. Chem. Phys. 126 243-253.

PVSZ88

Pavlov-Verevkin V.B., Sadovskii D.A., and Zhilinskií, B.I. [1988] On the dynamical meaning of the diabolic points. Europhys. Lett. 6 573-578.

PK98

Petrov, S.V. and Katsov, K.M. [1998] Chem. Phys. Let. 246:649-??.

PSZ89

Pierre G., Sadovskii D.A., and Zhilinskií, B.I. [1989] Organization of quantum bifurcations: crossover of rovibrational bands in spherical top molecules. Europhys. Lett. 10:409-414.

P87

Pollak, E. [1987] ?? J. Chem. Phys. 86:1645-??.

PF95

Prosmiti, R. and Farantos S.C. [1995] ?? J. Chem. Phys. 103:3299-??.

Rei94

Reich, S. [1994] Momentum Conserving Symplectic Integrators, Physica D 76, 375-383.

Rei98

Reich, S. [1998] Dynamical Systems, Numerical Integration, and Exponentially Small Estimates, Habilitationsschrift, Freie Universität Berlin.

Rei99a

Reich, S. [1999] Backward error analysis for numerical integrators, SIAM Numer. Anal., to appear.

Rei99b

Reich, S.[1999] Multi-symplectic collocation methods for Hamiltonian wave equations. UniS Preprint.

Rei99c

Reich, S. [1999] Multiple Time-Scales in Classical and Quantum-Classical Molecular Dynamics, J. Comput. Phys. 151, to appear

Ro70

Robinson, R. C. [1970] Generic properties of conservative systems. Amer. J. Math, 92:562-603.

Ro95

Robinson C. [1995] Dynamical Systems. CRC Press, Inc.

RdSD

Roberts, M., and de Sousa Dias, M.E.R.[1997] Bifurcations from relative equilibria of Hamiltonian systems. Nonlinearity 10, 1719-1738.

RTW92

Romagnoli, M., Trillo, S. and Wabnitz, S. [1992] Soliton switching in nonlinear couplers, Opt. Quant. Electron. 24, 1237-1267.

SDe96

Sadovskii, D. A., and D. Delos. [1996] Bifurcations of periodic orbits of Hamiltonian systems: Analysis using normal form theory. Phys. Rev. E. 54, 2033-2070.

SSDe95

Sadovskii, D. A., J. A. Shaw, and D. Delos. [1995] Organization of sequences of bifurcations of periodic orbits. Phys. Rev. Lett. 75, 2120-2123.

SFTZ93

Sadovskii D.A., N.G.Fulton, J.R.Tennyson, and Zhilinskií B. I. [1993] Nonlinear normal modes and local bending vibrationsi of H₃⁺ and D₃⁺. J.Chem.Phys. 99, 906-918.

SD88

Sadovskii D.A. and Zhilinskií, B.I. [1988] Qualitative analysis of vibration-rotation Hamiltonians for spherical top molecules. Mol. Phys. 65, 109-128.

SZ93a

Sadovskii D.A., and Zhilinskií, B.I. [1993] Group-theoretical and topological analysis of localized rotation-vibration states. Phys. Rev. A. 47, 2653-2671.

SZ93b

Sadovskii D.A., and Zhilinskií, B.I. [1993] Qualitative study of a model three-level Hamiltonian with SU(3) dynamical symmetry. Phys. Rev. A. 48, 1035-1044.

SZ95

Sadovskii D., Zhilinskií B. [1995] Counting levels within vibrational polyads. Generating function approach. J. Chem. Phys. 103, 10520-10536.

SZ98

Sadovskii D. A., and Zhilinskií B. I. [1998] Tuning the hydrogen atom in crossed fields between the Zeeman and Stark limits. Phys. Rev. A, 57:2867-2884.

SD99

Sadovskií, D.A. and Zhilinskií, B.I. [1999] Monodromy, diabolic points, and angular momentum coupling. Phys. Lett A in press.

SZCP90

Sadovskii D.A., Zhilinskii, B.I., Champion J.P., Pierre G. [1990] Manifestation of bifurcations and diabolic points in molecular energy spectra. J. Chem. Phys. 92:1523-1537.

SZM

Sadovskii, D. A., B. I. Zhilinskii, and L. Michel, [1996] Collapse of the Zeeman structure of the hydrogen atom in an external electric field. Phys. Rev. A 53:4064-4067.

SSC94

Sanz-Serna, J.M. and Calvo, M.P. [1994] Numerical Hamiltonian Systems, Chapman & Hall, London.

SY94

Sauer, T. and York, J.A. [1994] Rigorous Verification of Trajectories for the Computer Simulation of Dynamical Systems, Nonlinearity 4, 961-979.

Sch96

J. Scheurle [1996] Some aspects of successive bifurcation in the Couette-Taylor problem, Fields Institute Comm., 5, 335-345.

S98

Shkoller, S. [1998] Geometry and curvature of diffeomorohism groups with H^s-metric and mean hydrodynamics, Journ. Funct. Anal., 160, 337-365.

SLM91

Simo, J.C., Lewis, D.R. and Marsden, J.E. [1991] Stability of relative equilibria I: The reduced energy momentum method. Arch. Rat. Mech. Anal. 115:15-59.

SPM90

Simo, J.C., Posbergh, T.A. and Marsden, J.E. [1990] Stability of coupled rigid body and geometrically exact rods: block diagonalization and the energy momentum method. Physics Reports 193:280-360.

SPM91

Simo, J.C., Posbergh, T.A. and Marsden, J.E. [1991] Stability of relative equilibria II: Three dimensional elasticity. Arch. Rat. Mech. Anal. 115:61-100.

SL91

Sjamaar, R. and Lerman, E. [1991] Stratified symplectic spaces and reduction. Ann. of Math., 134:375-422.

SW90

Stegeman, G.I. and Wright, E.M. [1990] All-optical waveguide switching, Opt. Quant. Electron. 22:95-122.

Sto95

Stoffer, D. [1995] Variable steps for reversible methods, Computing 55, 1-22.

TZ97

Tien Zung, N. [1997] A note on focus-focus singularities, Differential Geometry and Applications 7:123-130.

UMGKML95

Usunov, I.M., Muschall, R., Gölles, M., Kivshar, Y.S., Malomed, B.A. and Lederer, F. [1995] Pulse switching in nonlinear fiber directional couplers, Phys. Rev. E 51:2527-2537.

VdBH98

Valkering, T.P., de Boer, P.T. and Hoekstra, H.J.W.M. [1998] Soliton dynamics in directional couplers, Physica D 123:223-234.

VvdM95

Vanderbauwhede, A. and van der Meer, J. C. [1995] General reduction method for periodic solutions near equilibria. In Normal Forms and Homoclinic Chaos, pages 273-294. Langford, W. F. and Nagata, W. eds. Fields Institute Communications, 4.

Via97

Viana, M. [1997] Stochastic Dynamics of Deterministic Systems, Instituto de Matemática Pura e Applicada (IMPA), Rio de Janeiro.

VNS97

Vu Ngoc San [1997] Formes normales semi-classiques des systèmes complèment intégrables au voisinage d'un point critque de l'application moment. Preprint, Insitut Fourier 377, 1997.

VNS98

Vu Ngoc San [1998] Bohr-Sommerfeld conditions for integrable systems with critical manifolds of focus-focus type. Preprint, Institute Fourier 433, 1998.

VNS99

Vu Ngoc San [1999] Quantum monodromy in integrable systems. To appear in Comm. Math. Phys.

WH74

Warming, R.F. and Hyett, B.J. [1974] The Modified Equation Approach to the Stability and Accuracy of Finite-Difference Methods, J. Comp. Phys. 14, 159-179.

W71

Weinstein, A. [1971] Perturbation of periodic manifolds of Hamiltonian systems. Bull. Amer. Math. Soc., 77(5):814-818.

W73

Weinstein, A. [1973] Lagrangian submanifolds and Hamiltonian systems. Ann. of Math., 98:377-410.

W73a

Weinstein, A. [1973] Normal forms for nonlinear Hamiltonian systems. Inventiones Math., 20:47-57.

Wil36

Williamson, J. [1936] On the algebraic problem concerning the normal forms of linear dynamical systems. Amer. J. Math., 58:141-163.

W33

Wolibner, W. [1933] Un théorème sur l'existence du mouvement plan d'un fluid parfait homogène, incompressible, pendant un temps infiniment longue, Math. Zeitschr. 37, 698-726.

WLM99

Wulff, C., Lamb J.S.W. and Melbourne I. [1999] Bifurcation from relative periodic orbits. Preprint.

Yo90

Yoshida, H. [1990] Construction of Higher Order Symplectic Integrators, Phys. Lett. A 150, 262-268.

Y63

Yudovich, V.I. [1963] Non-stationary flow of an ideal incompressible liquid, Zh. Vych. Mat. 3 (6), 1032-1066. English translation XXXXXX, 1407-1456.

Y95

Yudovich, V.I. [1995] Uniqueness theorem for the basic nonstationary problem in dynamics of ideal incompressible fluid, Math. Res. Lett. 2, 27-38.

Z89

Zhilinskií B.I. [1989] Qualitative analysis of vibrational polyads: N-mode case. Chem. Phys. 137:1-13.

Z91

Zhilinskií, B.I. [1991] Symmetry analysis of the qualitative intramolecular phenomena. Lecture Notes in Physics 382:487-489.

Z96

Zhilinskií, B.I. [1996] Topological and symmetry features of intramolecular dynamics through high-resolution molecular spectroscopy. Spectrochimica Acta A, 52:881-900.

ZB94

Zhilinskii B.I. and Brodersen S. [1994] The symmetry of the vibrational components in T_d molecules. J. Mol. Spectrosc. 163:326-338.

ZBM94

Zhilinskii B.I, Brodersen S., and Madsen M.[1993] The pattern of clusters in isolated vibrational components of CF₄ and the semiclassical model. J. Mol. Spectrosc. 160:192-216.

ZKP99

Zhilinskii B. I., Kozin I., and Petrov S. [1999] Correlation between asymmetric and spherical top: Imperfect quantum bifurcations. Spectrochimica Acta A, 55:1471-1484.

ZP87

Zhilinskii B.I. and Pavlichenkov, I.M. [1987] Critical phenomena in the rotational spectra. Sov. Phys. JETP 65:221-229.

ZP88

Zhilinskií, B.I. and Pavlichenkov, I.M. [1988] Critical phenomenon in the rotational spectra of water molecule. Opt. Spectrosc. (USSR) 64:413-414.

Z92

Zou, M. [1992] Monodromy in two degrees of freedom integrable systems. Journal of Geometry and Physics 10:37-45.