\[
\newcommand{\Arg}{\mathsf{Arg}}
\newcommand{\C}{\mathbb{C}}
\newcommand{\R}{\mathbb{R}}
\newcommand{\N}{\mathbb{N}}
\newcommand{\Z}{\mathbb{Z}}
\newcommand{\Im}{\mathsf{Im}}
\newcommand{\intd}{\,\mathsf{d}}
\newcommand{\Re}{\mathsf{Re}}
\newcommand{\ball}{\mathsf{B}}
\newcommand{\wind}{\mathsf{wind}}
\]
Week 1 Worksheet - Solutions
Home | Assessment | Notes | Index | Worksheets | Blackboard
Complex Numbers
- $|2i| = 2$. The arguments are $\frac{\pi}{2} + 2n \pi$ for any $n \in \Z$. $\Arg(2i) = \frac{\pi}{2}$.
- $|-1 - i \sqrt{3}| = \sqrt{(-1)^2 + (\sqrt{3})^2} = 2$. The arguments are $\frac{4 \pi}{3} + 2 n \pi$ for any $n \in \Z$. The principal argument is $\frac{-2 \pi}{3}$.
- $|-4| = 4$. The arguments are $-\pi + 2 n \pi$ for any $n \in \Z$. $\Arg(-4) = \pi$.
Arithmetic
-
Calculate using the rules of arithmetic.
\[
\begin{align*}
& (2+3i) * (-5 + i) \\
= & \Big( 2 \times (-5) - 3 \times 1 \Big) + i \Big( 2 \times 1 + 3 \times (-5) \Big) \\
= & -13 - 13i
\end{align*}
\]
- $-5 + 24i$
- $\dfrac{2+3i}{3-4i} * \dfrac{3+4i}{3+4i} = \dfrac{-6 + 17i}{25} = \dfrac{-6}{25} + \dfrac{17}{25}i$
- $\dfrac{1-5i}{3i-1} * \dfrac{-3i-1}{-3i-1} = \dfrac{-16 + 2i}{10} = -\dfrac{8}{5} + \dfrac{1}{5} i$
- $\dfrac{1-i}{1+i} * \dfrac{1-i}{1-i} - i + 2 = \dfrac{-2i}{2} - i + 2 = 2 - 2i$
- $-i$ (becuase $i * i = -1$)
Write $z = x+iy$ so that the equation becomes $x^2 - y^2 + 2xyi = -5 - 12i$. Real and imaginary parts must be equal, so $x^2 - y^2 = -5$ and $2xyi = 12i$. By inspection we can take $x = 2, y = 3$ or $x = -2, y = -3$. The solutions are $z = 2 + 3i$ and $z = -2 - 3i$.
Completing the square gives $(z + 2)^2 - 4 = -12 + 6i$ so $(z+2)^2 = -8 + 6i$. Writing $z+2 = x+iy$ gives the equations $x^2 - y^2 = -8$ and $2xyi = 6i$. By inspection, we can take $x = 1, y = 3$ or $x = -1, y = -3$. The solutions are therefore $-1+3i$ and $-3 - 3i$.
-
Calclate
\[
\begin{align*}
\Re(z+w) & = \Re((x+iy) + (u + iv)) \\
& = \Re((x+u) + i(y+v)) \\
& = x+u \\
& = \Re(z) + \Re(w)
\end{align*}
\]
-
Calculate
\[
\begin{align*}
\Im(z-w) & = \Re((x+iy) - (u + iv)) \\
& = \Re((x-u) + i(y-v)) \\
& = y-v \\
& = \Im(z) - \Im(w)
\end{align*}
\]
Take $z = w = i$. Then
\[
\Re(z) = \Re(w) = 0
\]
but $\Re(zw) = \Re(-1) = -1$. Also $\Im(z) = \Im(w) = 1$ but $\Im(zw) = \Im(-1) = 0$.
-
Calcuate
\[
\begin{align*}
\overline{z+w} & = \overline{(x+iy) + (u + iv)} \\
& = \overline{(x+u) + i(y+v)} \\
& = (x+u) - i(y+v) \\
& = \overline{z} + \overline{w}
\end{align*}
\]
-
Calcuate
\[
\begin{align*}
\overline{zw} & = \overline{(xu - yv) + i(xv + yu)} \\
& = (xu - yv) - i(xv + yu) \\
& = (x-iy)(u-iv) \\
& = \overline{z} \overline{w}
\end{align*}
\]
-
Calcuate
\[
\begin{align*}
\overline{1/z} & = \overline{\dfrac{x}{x^2+y^2} - i \dfrac{y}{x^2+y^2}} \\
& = \dfrac{x}{x^2+y^2} + i \dfrac{y}{x^2+y^2} \\
& = \dfrac{x}{x^2+(-y)^2} - i \dfrac{(-y)}{x^2+(-y)^2} \\
& = 1 / \overline{z}
\end{align*}
\]
- $z + \overline{z} = (x + iy) + (x - iy) = 2x = 2 \Re(z)$
- $z - \overline{z} = (x + iy) - (x - iy) = 2iy = 2i \Im(z)$
The case $n = 1$ is immediate. We assume
\[
(\cos \theta + i \sin \theta)^n = \cos(n \theta) + i \sin(n \theta)
\]
and calculate
\[
\begin{align*}
& (\cos \theta + i \sin \theta)^{n+1} \\
= & (\cos \theta + i \sin \theta)^n (\cos \theta + i \sin \theta) \\
= & (\cos(n \theta) + i \sin(n \theta))(\cos \theta + i \sin \theta) \\
= & (\cos(n \theta + \theta) + i \sin(n\theta + \theta)) \\
= & \cos((n+1)\theta) + i \sin((n+1)\theta)
\end{align*}
\]
because when we multiply complex numbers we add arguments and multiply moduli.
We have
\[
\begin{align*}
& \cos(3\theta) + i \sin(3\theta) \\
= & (\cos \theta + i \sin \theta)^3 \\
= & (\cos \theta)^3 + 3i (\cos \theta)^2 (\sin \theta) - 3 (\cos \theta)(\sin \theta)^2 - i(\sin \theta)^3
\end{align*}
\]
so equating real and imaginary parts tell us
\[
\cos(3\theta) = (\cos \theta)^3 - 3 (\cos \theta)(\sin \theta)^2
\]
and
\[
\sin(3\theta) = 3 (\cos \theta)^2(\sin \theta) - (\sin \theta)^3
\]
hold.
From
\[
\begin{align*}
& (\cos \theta + i \sin \theta)^4 \\
= & (\cos \theta)^4 + 4 i (\cos \theta)^3(\sin \theta) -6 (\cos \theta)^2 (\sin \theta)^2 - 4i (\cos \theta) (\sin \theta)^3 + (\sin \theta)^4
\end{align*}
\]
we get also that
\[
\cos (4\theta) = (\cos \theta)^4 - 6(\cos \theta)^2(\sin \theta)^2 - (\sin \theta)^4
\]
and
\[
\sin(4\theta) = 4 (\cos \theta)^3(\sin \theta) - 4 (\cos \theta)(\sin \theta)^3
\]
hold.
Write $z = r(\cos \theta + i \sin \theta)$. If $z^n = w_0$ then $|z|^n = |w_0|$ and $n \theta$ is an argument of $w_0$. Thus $n \theta = \Arg(w) + 2k \pi$ for some $k \in \Z$. This means
\[
\theta = \frac{\Arg(w) + 2 k \pi}{n}
\]
for some $k \in \Z$. Taking $k \in \{0,1,\dots,n-1\}$ gives all possible distinct $z$ as after that we repeat.
Take $z_1 = z_2 = -1 + i \sqrt{3}$. We have $\Arg(z_1) = \Arg(z_2) = \frac{2\pi}{3}$. But
\[
(-1 + i\sqrt{3})^2 = -2 - 2 \sqrt{3} i
\]
has principal argument $-\frac{2\pi}{3}$.
Distance and Limits
- Fix $\epsilon > 0$. There is $N \in \N$ such that $n \ge N$ guarantees $|z_n - a| < \epsilon$. If $n \ge N$ then $| |z_n| - |a| | \le |z_n - a| < \epsilon$ by the reverse triangle inequality.
- $|z_n| = |1+i|^n = (\sqrt{2})^n$ does not converge, so $z_n$ does not converge.
Calculate
\[
|z_n| = \dfrac{|(1+i)|^n}{n} = \dfrac{(\sqrt{2})^n}{n}
\]
and note that if $n$ is large enough then $(\sqrt{2})^{n/2} > n$ so $|z_n| \ge (\sqrt{2})^{n/2}$ which does not converge, so $z_n$ does not converge.
- $|z_n| = \dfrac{1}{|(1+i)^n|} = \dfrac{1}{(\sqrt{2})^n}$ converges to 0 so $z_n$ converges to 0.
- There is $K \in \N$ such that $|z| / \sqrt{n} < 1$ for all $n \ge K$. Now for $n \ge K$ we have
\[
\begin{align*}
& \left| \frac{z^n}{n!} \right| \\
= & \frac{|z|}{1} \frac{|z|}{2} \cdots \frac{|z|}{K-1} \frac{|z|}{K} \cdot \frac{|z|}{K+1} \cdots \frac{|z|}{n} \\
\le & \frac{|z|}{K!} \frac{1}{\sqrt{K+1}} \cdots \frac{1}{\sqrt{n}}
\end{align*}
\]
which converges to zero as $n \to \infty$.
Paths and Domains
Fix $1 \le c \le 2$. We calculate
\begin{align*}
\lim_{t \to c} \gamma(t) & = \lim_{t \to c} 4t^2 + 2it \\
& = 4 \lim_{t \to c} t^2 + 2i \lim_{t \to c} t \\
& = 4c^2 + 2ic = \gamma(c)
\end{align*}
using the limit laws, which proves $\gamma$ is continuous at $c$.
Since $1 \le c \le 2$ was arbitrary $\gamma$ is continuous on $[1,2]$.
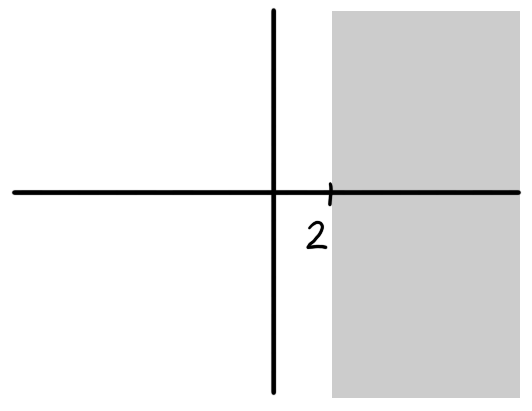
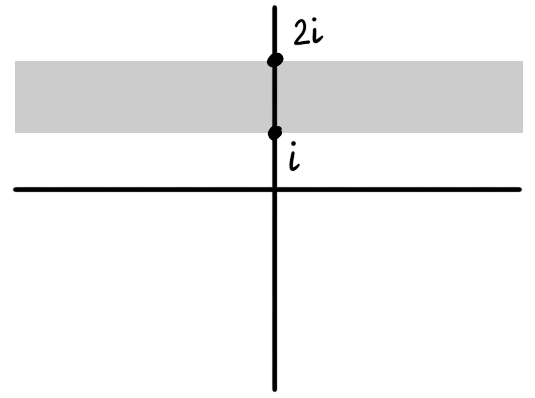
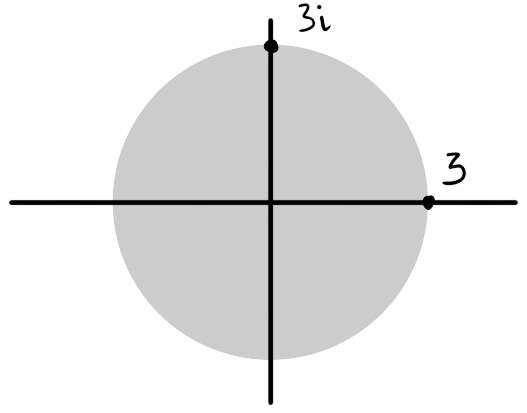
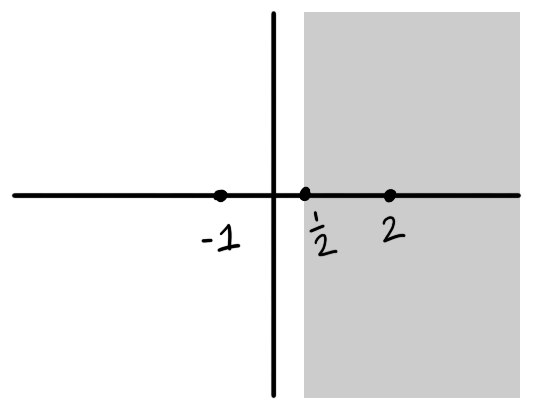
- Could be the image of a path.
- Could be the image of a path.
- Could not be the image of a path as it is not contiguous.
- Could be the image of a path.
Take
\[
\gamma(t) = (1-t)2 + t(i-1) = 2 + t(i-3)
\]
which is continuous and satisfies has $\gamma(0) = 2$ and $\gamma(1) = i-1$.

This is a domain as it is open and path connected.
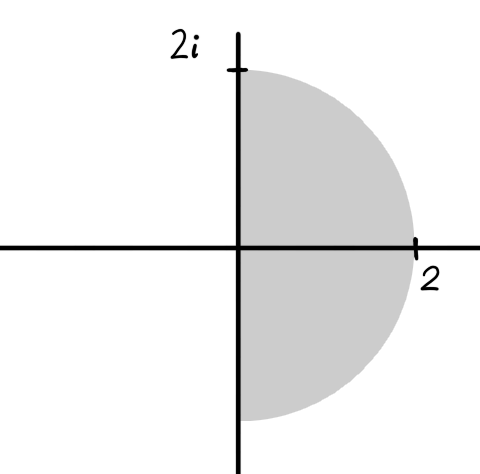
This is a domain as it is open and path connected.
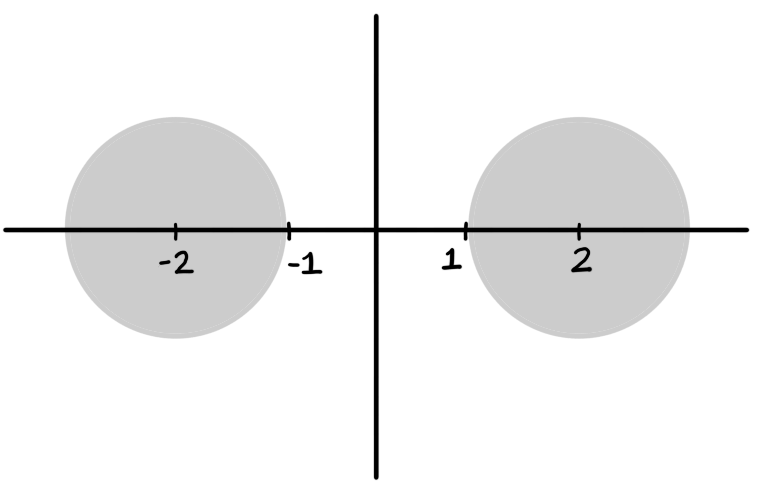
This is not a domain as it is not path connected.
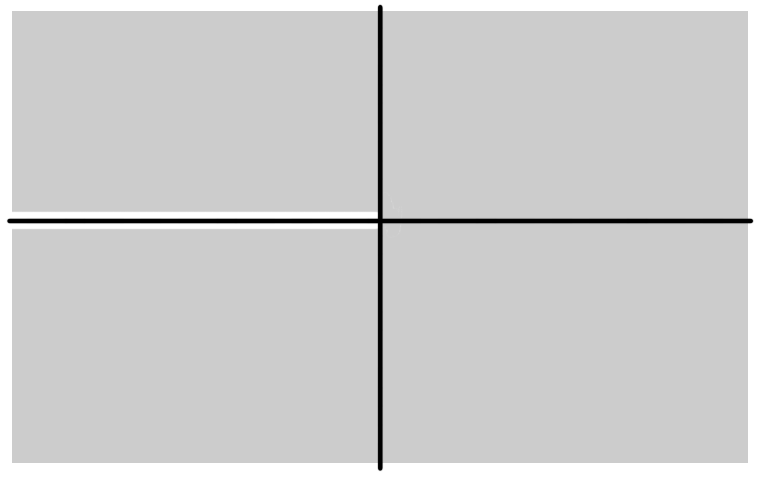
This is a domain as it is open and path connected.
- Fix $z \in E \cap F$. Since $E$ is open we can find $r > 0$ such that $\mathsf{B}(z,r) \subset E$. Since $F$ is open we can find $s > 0$ such that $\mathsf{B}(z,s) \subset F$. Put $t = \min \{r,s\}$. Then $\mathsf{B}(z,t) \subset E \cap F$. Since $z \in E \cap F$ was arbitrary, the intersection is open.

The red and blue sets above are both domains. However, their intersection is not path connected. The intersection of two domains need not be a domain.








