Week 1 Worksheet

Home | Assessment | Notes | Worksheets | Blackboard

Complex Numbers

1. Find the modulus, all arguments and the principal value of the argument for the following complex numbers.
   1. $2i$
   2. $1-i\sqrt{3}$
   3. $-4$
2. Draw the set of all $z \in \C$ satisfying the following conditions.
   1. $\Re(z) >2$
   2. $1 < \Im(z) < 2$
   3. $|z| < 3$
   4. $|z-2| < |z+1|$

Arithmetic

3. What is $2+3i$ multiplied by $-5+i$?
4. Write the following expressions in the form $x+iy$, $x,y\in\R$.
   1. $(3+4i)^2\vphantom{\dfrac{1}{1}}$
   2. $\dfrac{2+3i}{3-4i}$
   3. $\dfrac{1-5i}{3i-1}$
   4. $\dfrac{1-i}{1+i} -i+2$
   5. $\dfrac{1}{i}$
5. Find all solutions of the following equations.
   1. $z^2 = -5+12i$
   2. $z^2+4z+12-6i=0$
6. Let $z,w \in \C$. Prove the following statements.
   1. $\Re(z\pm w) = \Re(z)\pm\Re(w)$
   2. $\Im(z\pm w) = \Im(z) \pm \Im(w)$
7. Give examples to show that neither $\Re(zw)=\Re(z)\Re(w)$ nor $\Im(zw)=\Im(z)\Im(w)$ hold in general.
8. Fix $z,w \in \C$. Prove the following statements.
   1. $\overline{z\pm w} = \bar{z} \pm \bar{w}$
   2. $\overline{zw} =\bar{z}\bar{w}$
   3. $\overline{1 / z} = 1 / \overline{z}$ if $z \ne 0$
   4. $z+\bar{z}=2\Re(z)$
   5. $z-\bar{z} = 2i\Im(z)$
9. Recall that every non-zero $z \in \C$ can be written in polar form as $r( \cos \theta + i \sin \theta )$.
   1. Use induction on $n$ to derive \[ (\cos \theta + i \sin\theta)^n = \cos n\theta + i\sin n\theta \] for all $n \in \N$. (This is called de Moivre's Theorem.)
   2. Use De Moivre's Theorem to derive formulae for $\cos(3\theta)$, $\sin(3\theta)$, $\cos(4\theta)$, $\sin(4\theta)$ in terms of $\cos\theta$ and $\sin \theta$.
10. Let $w_0 \ne 0$ be a complex number such that $|w_0|=r$ and $\Arg(w_0) = \theta$. Find the polar forms of all the solutions $z$ to $z^n=w_0$, where $n \geq 1$ is a positive integer.
11. Let $\Arg(z)$ denote the principal value of the argument of $z$. Give an example to show that \[ \Arg(z_1z_2) \ne \Arg(z_1) + \Arg(z_2) \] in general.

Distance and Limits

12. A sequence $z_n$ in $\C$ is known to converge to $a$. Use the reverse triangle inequality to prove that $|z_n|$ converges to $|a|$.
13. Determine whether the following sequences converge.
    1. $z_n = (1+i)^n \vphantom{\dfrac{1}{1}}$
    2. $z_n = \dfrac{(1+i)^n}{n}$
    3. $z_n = \dfrac{1}{(1+i)^n}$
14. Prove that $z^n / n!$ converges to zero for every complex number $z \in \C$.

Paths and Domains

15. Verify that $\gamma(t) = 4t^2 + 2it$ on $[1,2]$ is continuous.
16. Which of the following could be the image of a path?
    1. 
    2. 
    3. 
    4. 
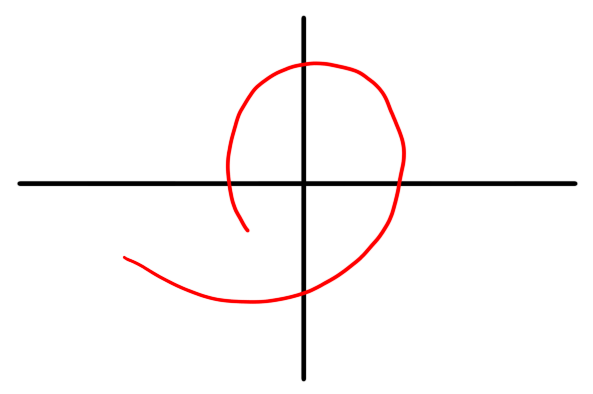
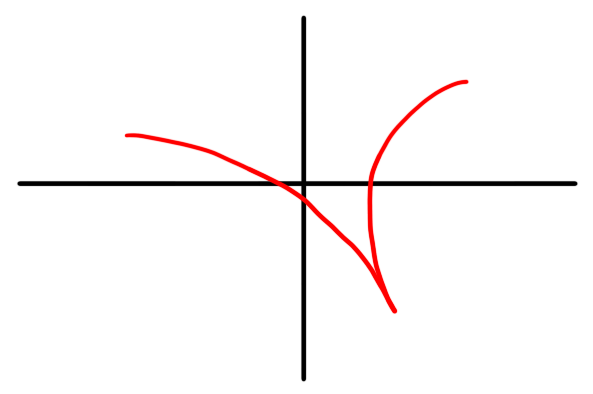
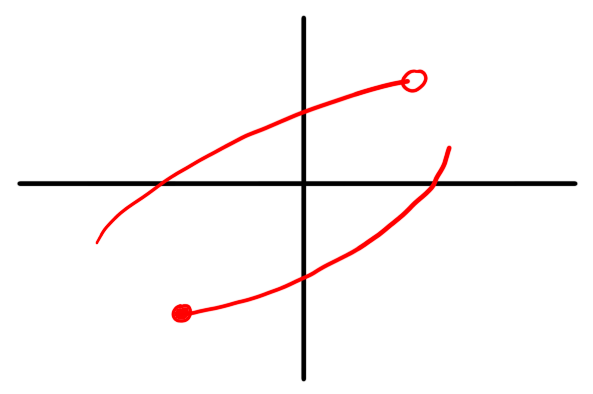
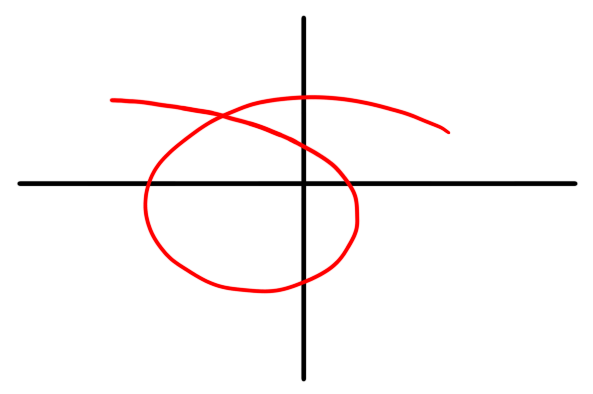
17. Write down a formula for a path $\gamma : [0,1] \to \C$ describing a path from $2$ to $i - 1$.
18. Sketch the following sets of complex numbers. Which of them are domains?
    1. $\{ z \in \C : \Im(z) > 0 \}$
    2. $\{ z \in \C : \Re(z) > 0 \textrm{ and } |z| < 2 \}$
    3. $\{ z \in \C : |z-2| < 1 \textup{ or } |z+2| < 1 \}$
    4. $\C \setminus \{ z \in \C : x\le 0 \textrm{ and } y = 0 \}$
19. Let $E$ and $F$ be open subsets of $\C$. Prove that $E \cap F$ is open.
20. Is the intersection of two domains always a domain? Either prove this or provide a counterexample.