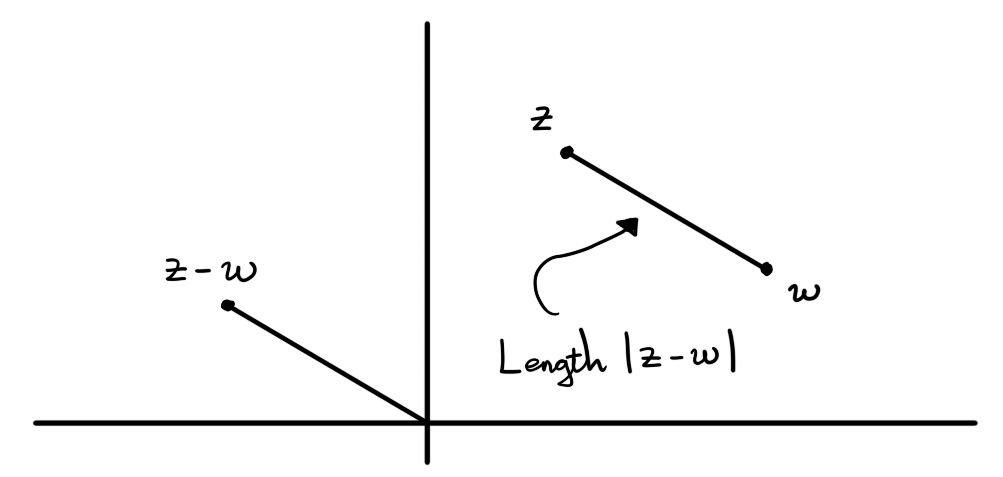
Figure 1: The distance between complex numbers $z$ and $w$ is defined to be $|z-w|$.
Home | Assessment | Notes | Worksheets | Blackboard
We can use the absolute value of a complex number to determine distance in the complex plane, and therefore to define what it means for a sequence of complex numbers to converge to a limit.
The distance between complex numbers $z,w \in \C$ is $|z-w|$.
The distance between two complex numbers as we have defined it here is the same as the Euclidean distance between the corresponding vectors in $\R^2$.
The open ball of radius $r > 0$ centered at $z \in \C$ is the set \[ \ball(z,r) = \{ w \in \C : |z-w| < r \} \] of all complex numbers $w$ within a distance of $r$ from $z$.
Open balls give us a notion of nearness. If complex numbers belong to an open ball of small radius then they are all close to the center of the ball.
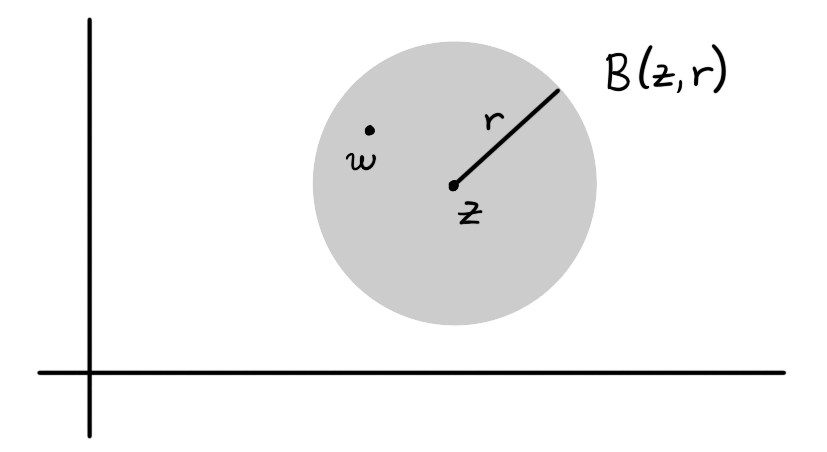
Figure 2: The open ball $\ball(z,r)$ centered at $z$ of radius $r$ is the shaded region of the plane. The point $w$ belongs to the ball.
The crucial definition in this section is what it means for a sequence of complex numbers to converge to a limiting complex number. Recall that a sequence of complex numbers is just an indexed list $z_1,z_2,z_3,\dots$ of complex numbers. Formally, a sequence is any function from $\N$ to $\C$.
A sequence $z_n$ of complex numbers converges to a complex number $a$ if, for every $\epsilon > 0$ one can find $N \in \N$ such that $n \ge N$ implies $|z_n - a| < \epsilon$.
When $z_n$ converges to $a$ we write $\displaystyle\lim_{n \to \infty} z_n = a$. This is equivalent to the real limit statement $\displaystyle\lim_{n \to \infty} |z_n - a| = 0$. We can interpret convergence in terms of open balls because $|z_n - a| < \epsilon$ is equivalent to $z_n \in \ball(a,\epsilon)$.
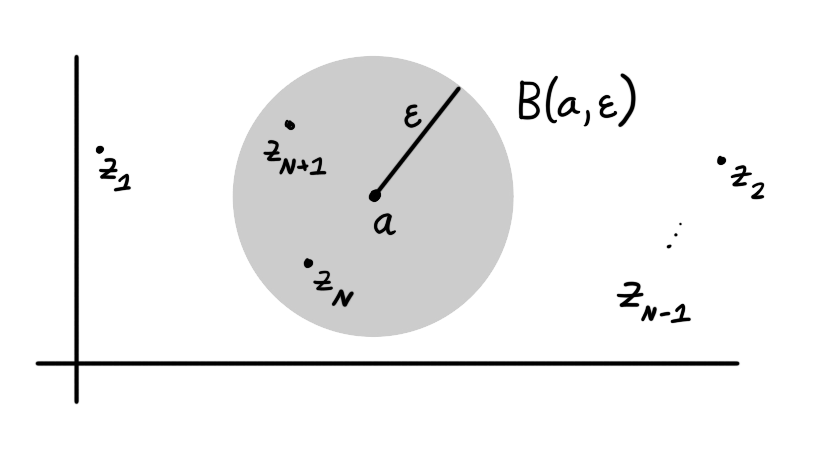
Figure 3: A sequence $z_n$ converges to $a$ if and only if, for every $\epsilon > 0$ there is $N \in \N$ such that $z_n \in \ball(a,\epsilon)$ for all $n \ge N$.
The sequence $z_n = \dfrac{1}{n+in^2}$ converges to 0.
Fix $\epsilon > 0$. We must produce $N \in \N$ with the property that $|z_n - 0| < \epsilon$ whenever $n \ge N$. First we calclate \[ \begin{align*} |z_n - 0| = \left| \frac{1}{n + in^2} \right| & = \left| \frac{n - in^2}{n^2 + n^4} \right| \\ & = \sqrt{ \left( \frac{n}{n^2 + n^4} \right)^2 + \left( \frac{-n^2}{n^2+n^4} \right)^2} \\ & = \sqrt{\frac{1}{n^2 + n^4}} \\ & \le \frac{1}{n} \end{align*} \] so that, if $n \ge N > \frac{1}{\epsilon}$ we automatically have $|z_n - 0| < \epsilon$.
If $\displaystyle\lim_{n \to \infty} z_n = a$ and $\displaystyle\lim_{n \to \infty} w_n = b$ then the following all hold.
The proofs of these results are exactly the same as in the real case. $\square$
Let $z_n \in \C$ for all $n \in \N$ and write $z_n = x_n + iy_n$. Then $z_n$ converges if and only if $x_n$ and $y_n$ converge.
Suppose that $z_n \rightarrow z$ and write $z=x+iy$. Then \[ |x_n-x| \leq \sqrt{ |x_n-x|^2 + |y_n-y|^2} = |z_n-z| \rightarrow 0 \] as $n\to\infty$. Hence $x_n \rightarrow x$. A similar argument show that $y_n \rightarrow y$.
Conversely, suppose that $x_n$ converges to $a$ and $y_n$ converges to $b$. Then \[ \lim_{n \to \infty} z_n = \lim_{n \to \infty} x_n + i \lim_{n \to \infty} y_n = a + ib \] so that $z_n \rightarrow a+ib$. $\square$
Next, we will talk about continuity of functions from intervals $[a,b] \subset \R$ to the complex plane. Informally, such a function is continuous if it can be drawn without lifting the pen from the paper. The formal definition involves limits.
Fix $a \le b $ real. A function $\gamma : [a,b] \to \C$ is continuous at $c \in [a,b]$ if \[\lim_{t \to c} \gamma(t) = \gamma(c)\] holds as a limit using the absolute value. We say that $\gamma$ is continuous if it is continuous at every $a \le c \le b$.
Formally, the expression \[\lim_{t \to c} \gamma(t) = \gamma(c)\] means the following: for every $\epsilon > 0$ there is $\delta > 0$ such that $|s - t| \l \delta$ implies $|\gamma(s) - \gamma(c)| \l \epsilon$. For the most part, we will take continity of functions given by simple formulae for granted. In such cases, continuity can be verified using the laws of limits. We finish with a discontinuous example.
The function defined on $[1,2]$ by \[\gamma(t) = \begin{cases} i+t & t < 1.5 \\ 1 + it & t \ge 1.5 \end{cases}\] is not a path.
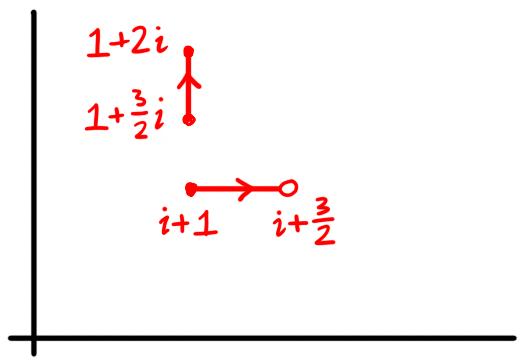
Figure 3: For $0 \le t < 1.5$ the function $\gamma$ traverses the horizontal segment and for $1.5 \le t \le 2$ it traverses the vertical segment. Since they are not joined together, we suspect $\gamma$ is not continuous.
To see this, we calculate the limits from the left and from the right as $t$ tends to $1.5$. We have \[ \begin{aligned} \lim_{t \to 1.5+} \gamma(t) & = \lim_{t \to 1.5+} 1 + it = 1 + \tfrac{3}{2} i \\ \lim_{t \to 1.5-} \gamma(t) & = \lim_{t \to 1.5-} i+t = \tfrac{3}{2} + i \end{aligned} \] and these limits are not the same, verifying what we suspect from the picture.