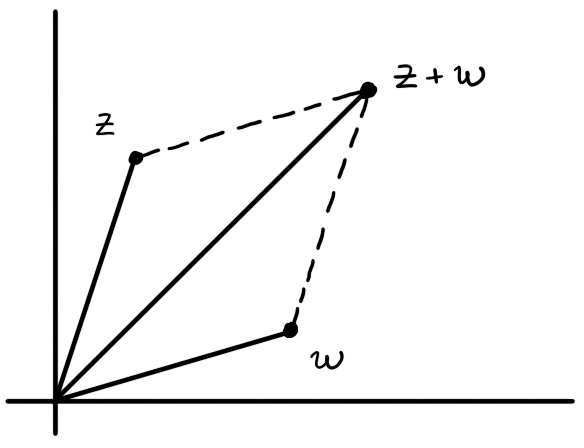
Figure 1: The complex numbers $z$ and $w$ can be thought of vectors in $\R^2$. Adding them as complex numbers is the same as adding the corresponding vectors.
Home | Assessment | Notes | Worksheets | Blackboard
In this section we will learn how to add, subtract, multiply and divide complex numbers, and comprehend addition and multiplication geometrically. We will represent complex numbers in polar form to develop a geometric picture of multiplication.
We define addition and subtraction of complex numbers as follows. \[ \begin{aligned} (x+iy) + (u+iv) &= (x+u) + i(y+v) \\ \\ (x+iy) - (u+iv) &= (x-u) + i(y-v) \end{aligned} \]
Note that the sums $x+u$, $y+v$ and the differences $x-u$, $y-v$ are sums and differences of real numbers, which we already know how to add and subtract.
Simplify the following.
We use the rules of addition and subtraction to write each expression in the form $x+iy$.
Writing complex numbers such as $(-1) + 0i$ and $0 + (-2)i$ will become cumbersone. We therefore adopt varions conventions to make writing easier. We will take for granted things like \[x - iy = x + i(-y)\] \[-x + iy = (-x) + iy\] \[yi = 0 + iy\] when writing complex numbers from now on.
Simplify the following.
We use the rules of addition and subtraction to write each expression in the form $x+iy$.
Addition of complex numbers can be thought of as addition of the corresponding vectors in $\R^2$.
Figure 1: The complex numbers $z$ and $w$ can be thought of vectors in $\R^2$. Adding them as complex numbers is the same as adding the corresponding vectors.
We define multiplication of complex numbers as follows. \[(x+iy) \cdot (u+iv) = (xu - yv) + i(xv + yu)\]
All the usual rules of arithmetic, like distribution, associativity and commutativity, apply to the arithmetic of complex numbers.
Simplify the following.
We use the definition of multiplication to write each expression in the form $x+iy$.
The polar representation give us a geometric picture of complex multiplication. Fix $z,w$ non-zero complex numbers with polar representations \[z = r \left( \cos(\theta) + i \sin(\theta) \right)\] \[w = s \left( \cos(\psi) + i \sin(\psi) \right)\] respectively. Multiplying $z \cdot w$ we get \[ \begin{aligned} z \cdot w & = r s \Big( \left( \cos(\phi) \cos(\psi) - \sin(\psi) \sin(\phi) \right) + i \left( \cos(\phi) \sin(\psi) + \cos(\psi) \sin(\phi) \right) \Big) \\ & = r s \Big( \cos(\phi + \psi) + i \sin(\phi + \psi) \Big) \end{aligned} \] from the sine and cosine angle addition formulae. This reveals the geometric picture for multiplication: we multiply lengths and add arguments.
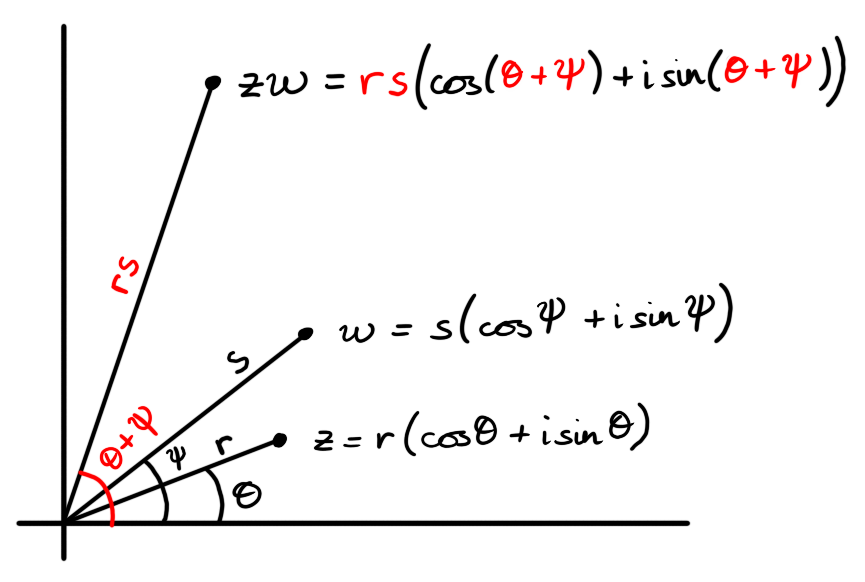
Figure 2: To multiply complex numbers we can simply multiply the lengths together and add the arguments.
We next look at reciprocals and division for complex numbers.
If $z \in \C$ is non-zero its inverse is \[ \frac{1}{z} = \frac{x}{x^2 + y^2} - i \frac{y}{x^2+y^2} \] which is also a complex number.
Calculate the inverse of $2 + i$.
We have \[ \dfrac{1}{2+i} = \dfrac{2}{5} - i \dfrac{1}{5} \] from the definition.
The inverse of a non-zero complex number $z$ is its inverse in the multiplicative sense. The calculation \[ \begin{aligned} z \cdot \frac{1}{z} & = (x + iy) \cdot \left( \frac{x}{x^2 + y^2} - i \frac{y}{x^2+y^2} \right) \\ & = \frac{ x^2 + y^2 }{x^2 + y^2} + i \frac{-xy + xy}{x^2 + y^2} \\ & = 1 \end{aligned} \] verifies that: every non-zero complex number has a multiplicative inverse.
For a geometric picture of the inverse we introduce conjugation.
The conjugate of a complex number $z=x+iy$ is the number $\overline{z} = x-iy$.
Figure 3: The conjugate of a complex number $z$ is the reflection of $z$ in the real axis.
We have \[ z \cdot \overline{z} = (x+iy)\cdot(x-iy) = x^2 + y^2 + i(-xy + yx)= |z|^2 \] so that \[ \dfrac{1}{z} = \dfrac{\overline{z}}{|z|^2} \] relating the conjugate to the absolute value.
Figure 4: The inverse of a non-zero complex number $z$ is a scaling of its conjugate.
With the rules of arithmetic - addition, subtraction, multiplication, and inverses - defined above $\C$ forms a number system or field.
Note that $\C$ contains within it the number system $\R$ of real numbers. Indeed, we can think of $x + 0 i$ as the real number $x$.
Note also, from the definition of multiplication, that \[ i \cdot i = (0 + i \cdot 1) \cdot (0 + i \cdot 1) = (0 - 1) + i(0) = -1 \] so $i^2 = -1$. Thus $\C$ is a field that contains both the field $\R$ of real numbers and a solution to the equation $x^2+1=0$.
The following relationships between arithmetic and the modulus will be used all the time.
Let $z,w \in \C$.
For 1. note that $|z| = 0$ if and only if $x^2 + y^2 = 0$. This is equivalent to $x = 0$ and $y = 0$ i.e. $z = 0$.
For 2. we fix $z = x+iy$ and $w = u + iv$ and calculate \[|z|^2 |w|^2 = (x^2 + y^2)(u^2 + v^2) = (xu)^2 + (xv)^2 + (yu)^2 + (yv)^2\] and \[|zw|^2 = (xu-yv)^2 + (xv + yu)^2 = (xu)^2 + (yv)^2 + (xv)^2 + (yu)^2\] to prove they are the same.
For 3. note that \[\left| \frac{1}{z} \right|^2 = \left( \frac{x}{x^2 + y^2} \right)^2 + \left( \frac{-y}{x^2 + y^2} \right)^2 = \frac{x^2 + y^2}{(x^2 + y^2)^2} = \frac{1}{|z|^2}\] or simply apply 2. with $w = 1/z$.
For 4. we calculate \[\begin{aligned} (|z| + |w|)^2 &= |z|^2 + |w|^2 + 2|z||w| \\ |z+w|^2 & = (z+w)(\overline{z} + \overline{w}) = |z|^2 + |w|^2 + z \overline{w} + \overline{z} w \end{aligned}\] so it suffices to prove that $z \overline{w} + \overline{z} w \le 2|z||w|$. Now \[z\overline{w} + \overline{z} w = (x+iy)(u - i v) + (x - i y)(u + iv) = 2 \Re(z \overline{w})\] and finally \[z\overline{w} + \overline{z} w = 2 \Re(z \overline{w}) \le 2 |z \overline{w}| = 2 |z| |w|\] using $|w| = |\overline{w}|$ and 2.
For 5. apply the triangle inequality with $z = Z-W$ and $w = W$ to get $|Z| \le |Z-W| + |W|$ and therefore $|Z| - |W| \le |Z-W|$. Repeating this argument with $Z$ and $W$ swapped gives also $|W| - |Z| \le |Z-W|$. Therefore \[| |Z| - |W| | = \max \{ |Z| - |W|, |W| - |Z| \} \le |Z| + |W|\] as desired. $\square$