\[
\newcommand{\Arg}{\mathsf{Arg}}
\newcommand{\C}{\mathbb{C}}
\newcommand{\R}{\mathbb{R}}
\newcommand{\N}{\mathbb{N}}
\newcommand{\Z}{\mathbb{Z}}
\newcommand{\Im}{\mathsf{Im}}
\newcommand{\intd}{\,\mathsf{d}}
\newcommand{\Re}{\mathsf{Re}}
\newcommand{\ball}{\mathsf{B}}
\newcommand{\wind}{\mathsf{wind}}
\newcommand{\Log}{\mathsf{Log}}
\]
Week 6 Worksheet
Home | Assessment | Notes | Index | Worksheets | Blackboard
Winding Numbers
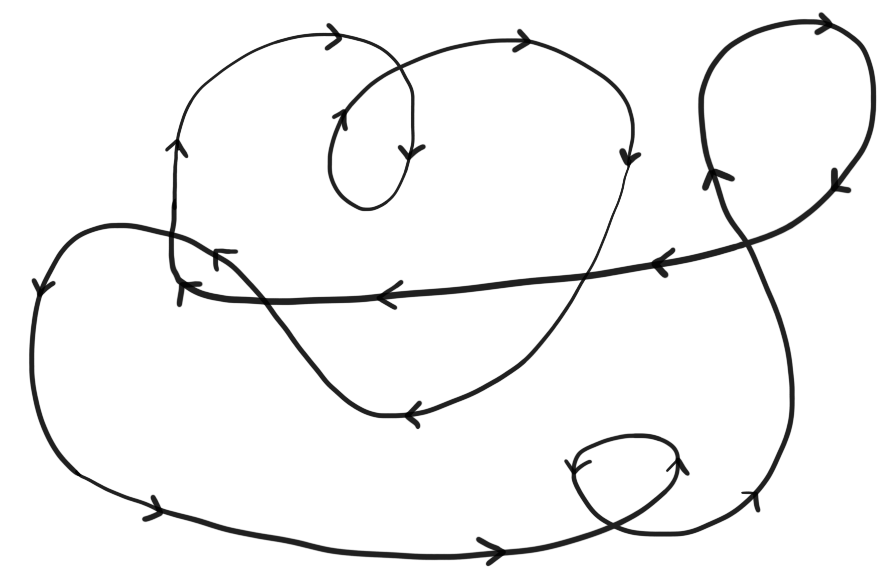
Calculate the winding number of the contour below around all points not on the path.
Cauchy's Theorem
- Let $\gamma_1(t) = -1+\frac{1}{2}e^{it}$ on $[0, 2\pi]$, let $\gamma_2(t) = 1+\frac{1}{2}e^{it}$ on $[0, 2\pi]$ and let $\gamma(t) = 2e^{-it}$ on $[0, 2\pi]$. Let $f(z)=1/(z^2-1)$. Use Cauchy Theorem to deduce that
\[
- \int\limits_{\gamma} f \intd z = \int\limits_{\gamma_1} f \intd z + \int\limits_{\gamma_2} f \intd z
\]
What is the contour integral of $f(z) = 1/z$ over the contour $\gamma$ shown below?
Fix distinct complex numbers $z_1$ and $z_2$ and contours $\gamma,\gamma_1,\gamma_2$ as in the figure. Suppose that $f : \C \setminus \{z_1,z_2 \} \to \C$ is holomorphic.
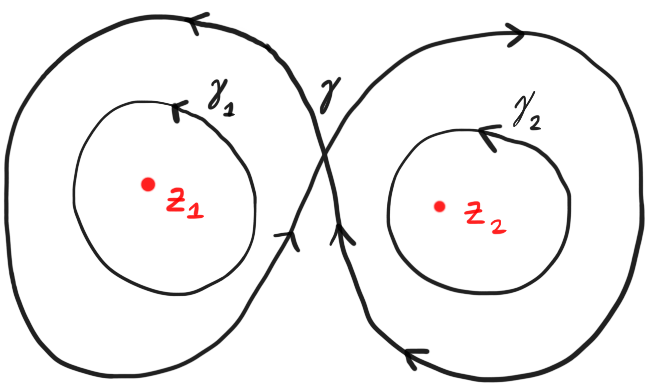
If $\displaystyle\int\limits_{\gamma_1} f = 3 + 4i$ and $\displaystyle\int\limits_{\gamma_2} f = 5 + 6i$ what is the value of $\displaystyle\int\limits_\gamma f$?
- Verify that
\[
f(z) = \begin{cases} \dfrac{\cos(z) - 1}{z} & z \ne 0 \\ 0 & z = 0 \end{cases}
\]
is holomorphic on $\C$. Then evaluate
\[
\int\limits_\gamma \dfrac{\cos(z)}{z} \intd z
\]
where $\gamma(t) = e^{it}$ on $[0,2\pi]$.