Week 2 Worksheet

Home | Assessment | Notes | Index | Worksheets | Blackboard

Paths

1. Verify that $\gamma(t) = 4t^2 + 2it$ on $[1,2]$ is continuous.
2. Which of the following could be the image of a path?
   1. 
   2. 
   3. 
   4. 
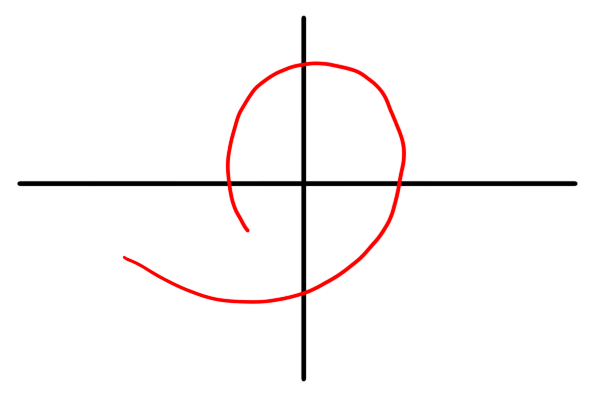
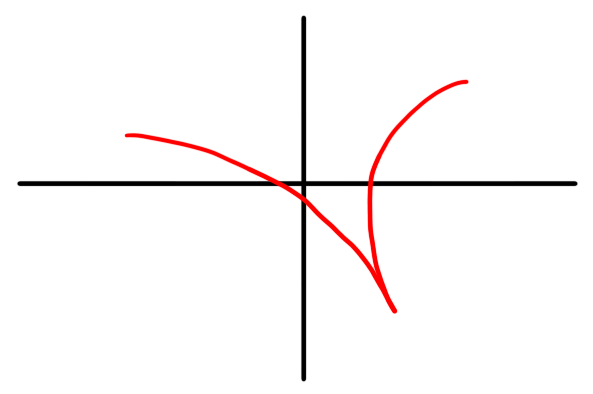
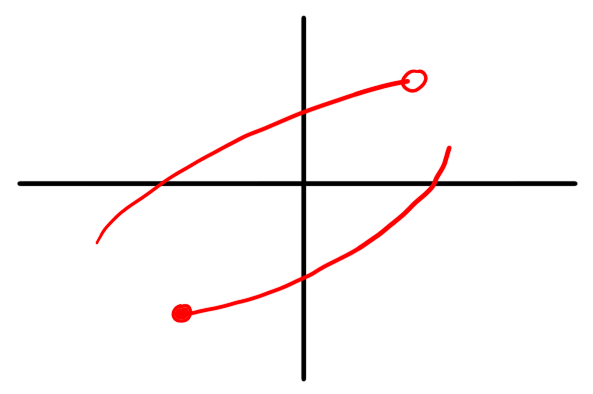
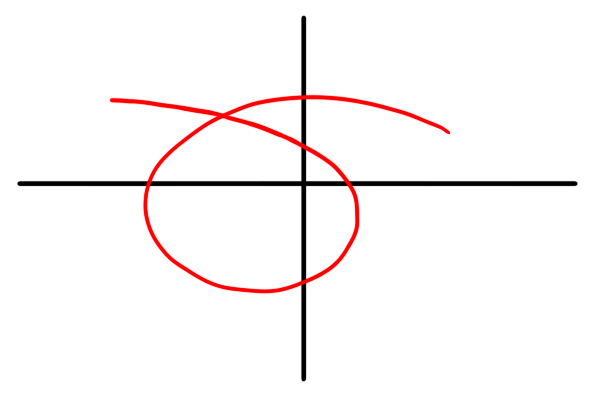
3. Write down a formula for a path $\gamma : [0,1] \to \C$ describing a path from $2$ to $i - 1$.

Domains

4. Sketch the following sets of complex numbers. Which of them are domains?
   1. $\{ z \in \C : \Im(z) > 0 \}$
   2. $\{ z \in \C : \Re(z) > 0 \textrm{ and } |z| < 2 \}$
   3. $\{ z \in \C : |z-2| < 1 \textup{ or } |z+2| < 1 \}$
   4. $\C \setminus \{ z \in \C : x\le 0 \textrm{ and } y = 0 \}$
5. Let $E$ and $F$ be open subsets of $\C$. Prove that $E \cap F$ is open.
6. Is the intersection of two domains always a domain? Either prove this or provide a counterexample.

Functions

7. What are the real and imaginary parts of $f(z) = \Re(z)$ and $f(z) = |z|$?
8. Let $f(z) = z^2$ on $\C$.
   1. Determine the real and imaginary parts of $f$.
   2. Calculate the gradients of $u$ and $v$. (Recall that \[ (\nabla h)(x,y) = \Big\langle (\partial_1 h)(x,y), (\partial_2 h)(x,y) \Big\rangle \] is the gradient of $h : \R^2 \to \R$.)
   3. Verify that $\nabla u$ and $\nabla v$ are perpendicular.
9. Let $f(z) = 1/z$ on $\C \setminus \{0\}$.
   1. What are the real and imaginary parts of $f$?
   2. What are the level curves of the real part?

Continuous Functions

10. Prove that $f(z) = 1/z$ is continuous on $\C \setminus \{0\}$.
11. For each of the following, determine the limit or explain why it does not exist.
    1. $\lim\limits_{z \to 0} \dfrac{|z|}{z}$
    2. $\lim\limits_{z \to 0} \dfrac{|z|^2}{z}$
    3. $\lim\limits_{z \to 0} \Arg(z)$
12. Prove that the following functions are continuous.
    1. $f(z) = \Re(z)$ on $\C$
    2. $f(z) = |z|$ on $\C$
    3. $f(z) = \Arg(z)$ on $\C \setminus (-\infty,0]$