Week 1 Worksheet - Solutions

Home | Assessment | Notes | Index | Worksheets | Blackboard

Complex Numbers

1. 1. $|2i| = 2$. The arguments are $\frac{\pi}{2} + 2n \pi$ for any $n \in \Z$. $\Arg(2i) = \frac{\pi}{2}$.
   2. $|-1 - i \sqrt{3}| = \sqrt{(-1)^2 + (\sqrt{3})^2} = 2$. The arguments are $\frac{4 \pi}{3} + 2 n \pi$ for any $n \in \Z$. The principal argument is $\frac{-2 \pi}{3}$.
   3. $|-4| = 4$. The arguments are $-\pi + 2 n \pi$ for any $n \in \Z$. $\Arg(-4) = \pi$.
2. 1. 
   2. 
   3. 
   4. 

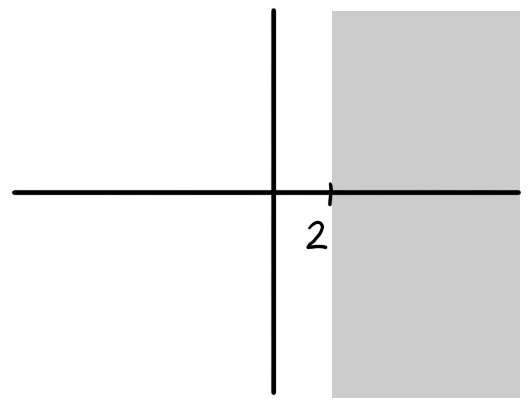
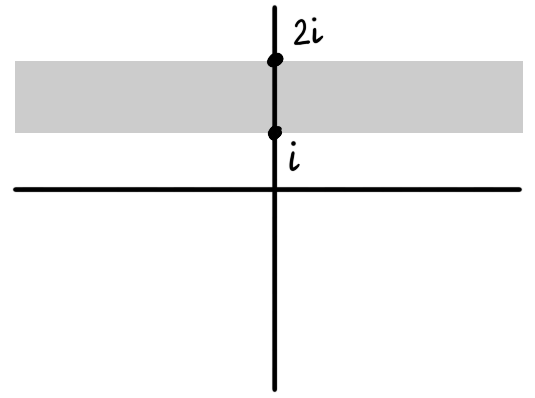
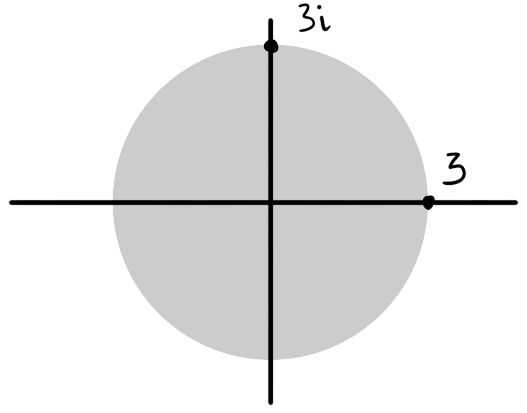
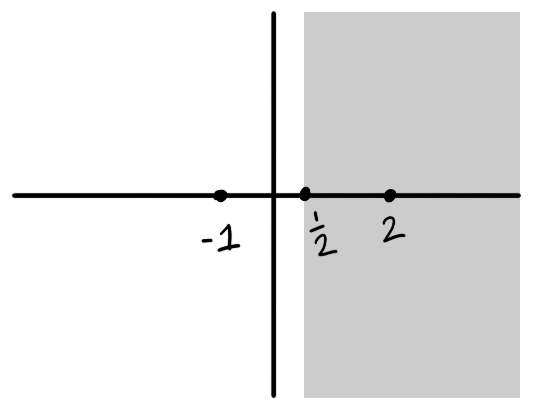
Arithmetic

3. Calculate using the rules of arithmetic. \[ \begin{align*} & (2+3i) * (-5 + i) \\ = & \Big( 2 \times (-5) - 3 \times 1 \Big) + i \Big( 2 \times 1 + 3 \times (-5) \Big) \\ = & -13 - 13i \end{align*} \]
4. 1. $-5 + 24i$
   2. $\dfrac{2+3i}{3-4i} * \dfrac{3+4i}{3+4i} = \dfrac{-6 + 17i}{25} = \dfrac{-6}{25} + \dfrac{17}{25}i$
   3. $\dfrac{1-5i}{3i-1} * \dfrac{-3i-1}{-3i-1} = \dfrac{-16 + 2i}{10} = -\dfrac{8}{5} + \dfrac{1}{5} i$
   4. $\dfrac{1-i}{1+i} * \dfrac{1-i}{1-i} - i + 2 = \dfrac{-2i}{2} - i + 2 = 2 - 2i$
   5. $-i$ (becuase $i * i = -1$)

5. 1. Write $z = x+iy$ so that the equation becomes $x^2 - y^2 + 2xyi = -5 - 12i$. Real and imaginary parts must be equal, so $x^2 - y^2 = -5$ and $2xyi = 12i$. By inspection we can take $x = 2, y = 3$ or $x = -2, y = -3$. The solutions are $z = 2 + 3i$ and $z = -2 - 3i$.

   2. Completing the square gives $(z + 2)^2 - 4 = -12 + 6i$ so $(z+2)^2 = -8 + 6i$. Writing $z+2 = x+iy$ gives the equations $x^2 - y^2 = -8$ and $2xyi = 6i$. By inspection, we can take $x = 1, y = 3$ or $x = -1, y = -3$. The solutions are therefore $-1+3i$ and $-3 - 3i$.

6. 1. Calclate \[ \begin{align*} \Re(z+w) & = \Re((x+iy) + (u + iv)) \\ & = \Re((x+u) + i(y+v)) \\ & = x+u \\ & = \Re(z) + \Re(w) \end{align*} \]
   2. Calculate \[ \begin{align*} \Im(z-w) & = \Re((x+iy) - (u + iv)) \\ & = \Re((x-u) + i(y-v)) \\ & = y-v \\ & = \Im(z) - \Im(w) \end{align*} \]

7. Take $z = w = i$. Then \[ \Re(z) = \Re(w) = 0 \] but $\Re(zw) = \Re(-1) = -1$. Also $\Im(z) = \Im(w) = 1$ but $\Im(zw) = \Im(-1) = 0$.

8. 1. Calcuate \[ \begin{align*} \overline{z+w} & = \overline{(x+iy) + (u + iv)} \\ & = \overline{(x+u) + i(y+v)} \\ & = (x+u) - i(y+v) \\ & = \overline{z} + \overline{w} \end{align*} \]

   2. Calcuate \[ \begin{align*} \overline{zw} & = \overline{(xu - yv) + i(xv + yu)} \\ & = (xu - yv) - i(xv + yu) \\ & = (x-iy)(u-iv) \\ & = \overline{z} \overline{w} \end{align*} \]

   3. Calcuate \[ \begin{align*} \overline{1/z} & = \overline{\dfrac{x}{x^2+y^2} - i \dfrac{y}{x^2+y^2}} \\ & = \dfrac{x}{x^2+y^2} + i \dfrac{y}{x^2+y^2} \\ & = \dfrac{x}{x^2+(-y)^2} - i \dfrac{(-y)}{x^2+(-y)^2} \\ & = 1 / \overline{z} \end{align*} \]

   4. $z + \overline{z} = (x + iy) + (x - iy) = 2x = 2 \Re(z)$
   5. $z - \overline{z} = (x + iy) - (x - iy) = 2iy = 2i \Im(z)$

9. 1. The case $n = 1$ is immediate. We assume \[ (\cos \theta + i \sin \theta)^n = \cos(n \theta) + i \sin(n \theta) \] and calculate \[ \begin{align*} & (\cos \theta + i \sin \theta)^{n+1} \\ = & (\cos \theta + i \sin \theta)^n (\cos \theta + i \sin \theta) \\ = & (\cos(n \theta) + i \sin(n \theta))(\cos \theta + i \sin \theta) \\ = & (\cos(n \theta + \theta) + i \sin(n\theta + \theta)) \\ = & \cos((n+1)\theta) + i \sin((n+1)\theta) \end{align*} \] because when we multiply complex numbers we add arguments and multiply moduli.

   2. We have \[ \begin{align*} & \cos(3\theta) + i \sin(3\theta) \\ = & (\cos \theta + i \sin \theta)^3 \\ = & (\cos \theta)^3 + 3i (\cos \theta)^2 (\sin \theta) - 3 (\cos \theta)(\sin \theta)^2 - i(\sin \theta)^3 \end{align*} \] so equating real and imaginary parts tell us \[ \cos(3\theta) = (\cos \theta)^3 - 3 (\cos \theta)(\sin \theta)^2 \] and \[ \sin(3\theta) = 3 (\cos \theta)^2(\sin \theta) - (\sin \theta)^3 \] hold.

      From \[ \begin{align*} & (\cos \theta + i \sin \theta)^4 \\ = & (\cos \theta)^4 + 4 i (\cos \theta)^3(\sin \theta) -6 (\cos \theta)^2 (\sin \theta)^2 - 4i (\cos \theta) (\sin \theta)^3 + (\sin \theta)^4 \end{align*} \] we get also that \[ \cos (4\theta) = (\cos \theta)^4 - 6(\cos \theta)^2(\sin \theta)^2 - (\sin \theta)^4 \] and \[ \sin(4\theta) = 4 (\cos \theta)^3(\sin \theta) - 4 (\cos \theta)(\sin \theta)^3 \] hold.

10. Write $z = r(\cos \theta + i \sin \theta)$. If $z^n = w_0$ then $|z|^n = |w_0|$ and $n \theta$ is an argument of $w_0$. Thus $n \theta = \Arg(w) + 2k \pi$ for some $k \in \Z$. This means \[ \theta = \frac{\Arg(w) + 2 k \pi}{n} \] for some $k \in \Z$. Taking $k \in \{0,1,\dots,n-1\}$ gives all possible distinct $z$ as after that we repeat.

11. Take $z_1 = z_2 = -1 + i \sqrt{3}$. We have $\Arg(z_1) = \Arg(z_2) = \frac{2\pi}{3}$. But \[ (-1 + i\sqrt{3})^2 = -2 - 2 \sqrt{3} i \] has principal argument $-\frac{2\pi}{3}$.

Sequences

12. Fix $\epsilon > 0$. There is $N \in \N$ such that $n \ge N$ guarantees $|z_n - a| < \epsilon$. If $n \ge N$ then $| |z_n| - |a| | \le |z_n - a| < \epsilon$ by the reverse triangle inequality.
13. 1. $|z_n| = |1+i|^n = (\sqrt{2})^n$ does not converge, so $z_n$ does not converge.

    2. Calculate \[ |z_n| = \dfrac{|(1+i)|^n}{n} = \dfrac{(\sqrt{2})^n}{n} \] and note that if $n$ is large enough then $(\sqrt{2})^{n/2} > n$ so $|z_n| \ge (\sqrt{2})^{n/2}$ which does not converge, so $z_n$ does not converge.

    3. $|z_n| = \dfrac{1}{|(1+i)^n|} = \dfrac{1}{(\sqrt{2})^n}$ converges to 0 so $z_n$ converges to 0.
14. There is $K \in \N$ such that $|z| / \sqrt{n} < 1$ for all $n \ge K$. Now for $n \ge K$ we have \[ \begin{align*} & \left| \frac{z^n}{n!} \right| \\ = & \frac{|z|}{1} \frac{|z|}{2} \cdots \frac{|z|}{K-1} \frac{|z|}{K} \cdot \frac{|z|}{K+1} \cdots \frac{|z|}{n} \\ \le & \frac{|z|}{K!} \frac{1}{\sqrt{K+1}} \cdots \frac{1}{\sqrt{n}} \end{align*} \] which converges to zero as $n \to \infty$.

Series

15. Let's look at the partial sums. Write $N = 4j + k$ where $1 \le k \le 4$. Then \[ \begin{align*} \sum_{n=1}^N i^n ={} & (i + i^2 + i^3 + i^4) + \cdots \\ & \quad {}+{} (i^{4j-3} + i^{4j-2} + i^{4j-1} + i^{4j}) \\ & \quad {}+{} (i^{4j+1} + \cdots + i^{4j+k}) \end{align*} \] is either $i$, $i-1$, $-1$ or $0$. That is \[ \sum_{n=1}^N i^n = \begin{cases} 0 & N = 4k \\ i & N = 4k+1 \\ i-1 & N = 4k+2 \\ -1 & N = 4k+3 \end{cases} \] and the partial sums do not converge.
16. From $|2/(3+i)| = 2/\sqrt{10} < 1$ we can apply the geometric series formula to get \[ \dfrac{\dfrac{2}{3+i}}{1 - \dfrac{2}{3+i}} - 1 = \dfrac{2}{1+i} - 1 = -i \] as the limit. (We subtract 1 because the series began at $n=1$.)
17. Yes, but this is not easy to prove from the tools we have, because we cannot compare this series with the geometric series. (The ratio and root tests are not conclusive.) We can write \[ \frac{1}{n^2} \le \frac{1}{n(n-1)} = \frac{1}{n-1} - \frac{1}{n} \] so that \[ \sum_{n=1}^N \frac{1}{n^2} \le 1 + \sum_{n=2}^N \frac{1}{n-1} - \frac{1}{n} = 1 + 1 - \frac{1}{N} \] is increasing and bounded. Therefore the partial sums converge.
18. For every $N \in \N$ we have \[ \Re \left( \sum_{n=1}^N z_n \right) = \sum_{n=1}^N \Re(z_n) \qquad \Im \left( \sum_{n=1}^N z_n \right) = \sum_{n=1}^N \Im(z_n) \] so the statement is a consequence of our theorem about convergence of sequences in terms of their real and imaginary parts.