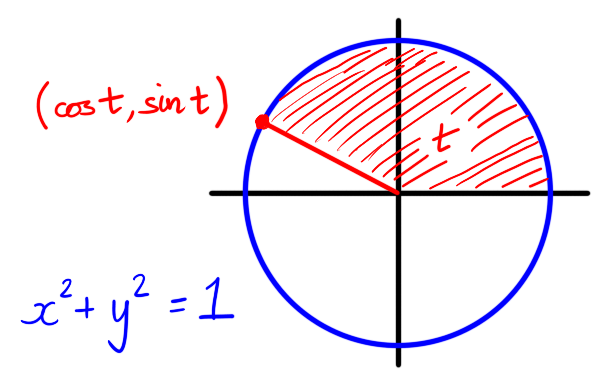
Figure 1: When $t$ is real $(\cos(t), \sin(t))$ lies on the unit circle $x^2 + y^2 = 1$. The area swept out from the positive horizontal axis is $t$.
Home | Assessment | Notes | Index | Worksheets | Blackboard
There are many ways to define the trigonometric functions cosine and sine. Here we will define them by power series. Put \[\begin{aligned} \cos(z) & = \sum_{n=0}^\infty (-1)^n \frac{z^{2n}}{(2n)!} = 1 - \frac{z^2}{2!} + \frac{z^4}{4!} - \frac{z^6}{6!} + \cdots \\ \sin(z) & = \sum_{n=0}^\infty (-1)^n \frac{z^{2n+1}}{(2n+1)!} = z - \frac{z^3}{3!} + \frac{z^5}{5!} - \frac{z^7}{7!} + \cdots \end{aligned}\] which both have infinite radius of convergence by comparison with the power series of the exponential function. Algebraic manipulations and our theorem on differentation of power series give all of the following properties for all $z \in \C$.
Next we prove two further properties of trigonometric functions that remain true in complex analysis.
For every $z \in \C$ we have $\cos(z) + i \sin(z) = \exp(iz)$.
From the power series definitions we have \[\begin{aligned} \exp(iz) &= \sum_{n=0}^\infty \frac{(iz)^n}{n!} \\ &= \sum_{j=0}^\infty \frac{(iz)^{4j}}{(4j)!} + \sum_{j=0}^\infty \frac{(iz)^{4j+1}}{(4j+1)!} + \sum_{j=0}^\infty \frac{(iz)^{4j+2}}{(4j+2)!} + \sum_{j=0}^\infty \frac{(iz)^{4j+3}}{(4j+3)!} \\ &= \sum_{j=0}^\infty \frac{z^{4j}}{(4j)!} + i \sum_{j=0}^\infty \frac{z^{4j+1}}{(4j+1)!} - \sum_{j=0}^\infty \frac{z^{4j+2}}{(4j+2)!} - i \sum_{j=0}^\infty \frac{z^{4j+3}}{(4j+3)!} \\ &= \cos(z) + i \sin(z) \end{aligned}\] because $i^4 = 1$. $\square$
We have $(\sin(z))^2 + (\cos(z))^2 = 1$ for all $z \in \C$.
From the previous theorem and preceding properties we have \[ \begin{gather*} \cos(z) = \frac{\exp(iz) + \exp(-iz)}{2}\\ \sin(z) = \frac{\exp(iz) - \exp(-iz)}{2i} \end{gather*}\] and so \[\begin{gather*} (\cos(z))^2 = \frac{\exp(2iz) + 2 + \exp(-2iz)}{4} \\ (\sin(z))^2 = \frac{\exp(2iz) - 2 + \exp(-2iz)}{-4} \end{gather*}\] which sum to 1. $\square$
Having introduced trigonometric functions as power series, it is not immediately clear how they are related to right-triangles. We can see from the power series definitions that $\cos(x)$ and $\sin(x)$ are real whenever $x$ is real. Since in particular $(\cos(x))^2 + (\sin(x))^2 = 1$ holds for all $x \in \R$ we can think of the point $(\cos(x),\sin(x))$ as belonging to the unit circle for all $x \in \R$. One can continue along these lines to define the number $\pi$.

Figure 1: When $t$ is real $(\cos(t), \sin(t))$ lies on the unit circle $x^2 + y^2 = 1$. The area swept out from the positive horizontal axis is $t$.
In particular, if $t = \pi$ we have $\exp(i \pi) = \cos(\pi) + i \sin(\pi) = 1$. Writing $e^{it} = \exp(it)$ we get Euler's famous relationship $e^{i\pi} = -1$.
We'll conclude this section by trying to understand $\cos(it)$ and $\sin(it)$ for $t \in \R$. Using \[\cos(z) = \frac{\exp(iz) + \exp(-iz)}{2} \qquad \sin(z) = \frac{\exp(iz) - \exp(-iz)}{2i}\] and replacing $z$ with $it$ for $t$ real gives \[\cos(it) = \frac{\exp(-t) + \exp(t)}{2} \qquad \sin(it) = \frac{\exp(-t) - \exp(t)}{2i}\] which reveals a relationship with the hyperbolic functions.
Define the hyperbolic functions $\cosh$ and $\sinh$ by \[\begin{aligned} \cosh(z) & = \frac{\exp(z) + \exp(-z)}{2} = \sum_{n=0}^\infty \frac{z^{2n}}{(2n)!} = 1 + \frac{z^2}{2!} + \frac{z^4}{4!} + \frac{z^6}{6!} + \cdots \\ \sinh(z) & = \frac{\exp(z) - \exp(-z)}{2} = \sum_{n=0}^\infty \frac{z^{2n+1}}{(2n+1)!} = z + \frac{z^3}{3!} + \frac{z^5}{5!} + \frac{z^7}{7!} + \cdots \end{aligned}\] for all $z \in \C$.
Algebraic manipulations and our theorem on differentation of power series give all of the following properties for all $z \in \C$.
We have $\cosh(z) + \sinh(z) = \exp(z)$ for all $z \in \C$.
This follows from adding the definitions together. $\square$
We have $(\cosh(z))^2 - (\sinh(z))^2 = 1$ for all $z \in \C$.
This is an exercise. $\square$
In particular, when $t$ is real the point $(\sinh(t),\cosh(t))$ belongs to the unit hyperbola $x^2 - y^2 = 1$.