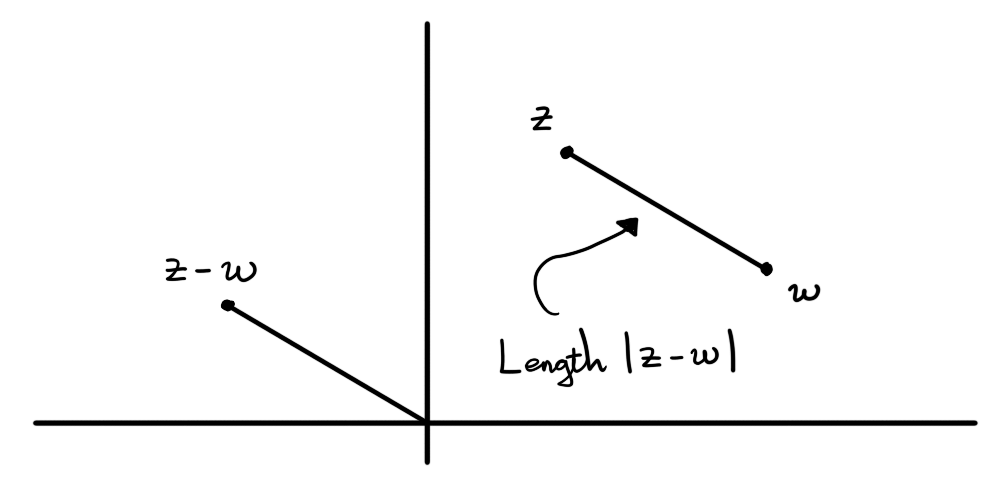
Figure 1: The distance between complex numbers $z$ and $w$ is defined to be $|z-w|$.
Home | Assessment | Notes | Index | Worksheets | Blackboard
We can use the absolute value of a complex number to determine distance in the complex plane, and therefore to define what it means for a sequence of complex numbers to converge to a limit.
The distance between complex numbers $z,w \in \C$ is $|z-w|$.
Figure 1: The distance between complex numbers $z$ and $w$ is defined to be $|z-w|$.
The distance between two complex numbers as we have defined it here is the same as the Euclidean distance between the corresponding vectors in $\R^2$.
The open ball of radius $r > 0$ centered at $z \in \C$ is the set \[ \ball(z,r) = \{ w \in \C : |z-w| < r \} \] of all complex numbers $w$ within a distance of $r$ from $z$.
Open balls give us a notion of nearness. If complex numbers belong to an open ball of small radius then they are all close to the center of the ball.
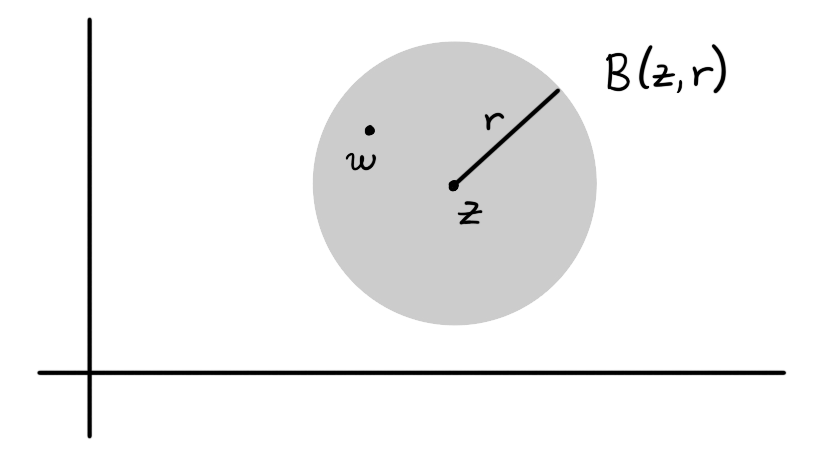
Figure 2: The open ball $\ball(z,r)$ centered at $z$ of radius $r$ is the shaded region of the plane. The point $w$ belongs to the ball.
The crucial definition in this section is what it means for a sequence of complex numbers to converge to a limiting complex number. Recall that a sequence of complex numbers is just an indexed list $z_1,z_2,z_3,\dots$ of complex numbers. Formally, a sequence is any function from $\N$ to $\C$.
A sequence $z_n$ of complex numbers converges to a complex number $a$ if, for every $\epsilon > 0$ one can find $N \in \N$ such that $n \ge N$ implies $|z_n - a| < \epsilon$.
When $z_n$ converges to $a$ we write $\displaystyle\lim_{n \to \infty} z_n = a$. This is equivalent to the real limit statement $\displaystyle\lim_{n \to \infty} |z_n - a| = 0$. We can interpret convergence in terms of open balls because $|z_n - a| < \epsilon$ is equivalent to $z_n \in \ball(a,\epsilon)$.
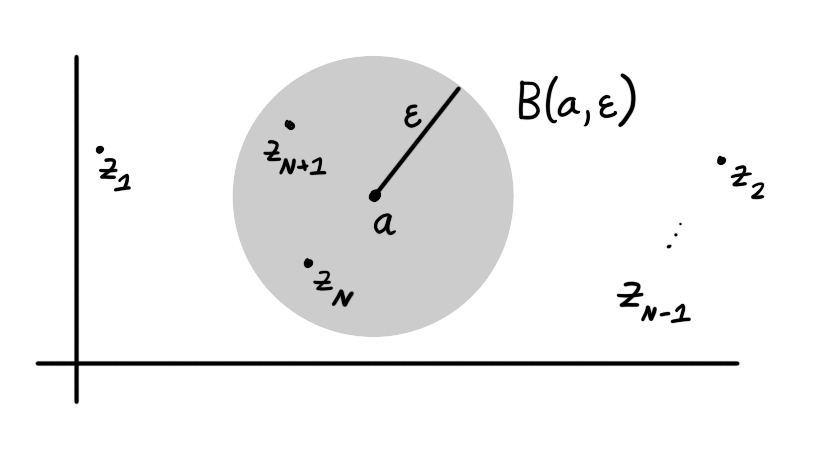
Figure 3: A sequence $z_n$ converges to $a$ if and only if, for every $\epsilon > 0$ there is $N \in \N$ such that $z_n \in \ball(a,\epsilon)$ for all $n \ge N$.
The sequence $z_n = \dfrac{1}{n+in^2}$ converges to 0.
Fix $\epsilon > 0$. We must produce $N \in \N$ with the property that $|z_n - 0| < \epsilon$ whenever $n \ge N$. First we calclate \[ \begin{align*} |z_n - 0| = \left| \frac{1}{n + in^2} \right| & = \left| \frac{n - in^2}{n^2 + n^4} \right| \\ & = \sqrt{ \left( \frac{n}{n^2 + n^4} \right)^2 + \left( \frac{-n^2}{n^2+n^4} \right)^2} \\ & = \sqrt{\frac{1}{n^2 + n^4}} \\ & \le \frac{1}{n} \end{align*} \] so that, if $n \ge N > \frac{1}{\epsilon}$ we automatically have $|z_n - 0| < \epsilon$.
If $\displaystyle\lim_{n \to \infty} z_n = a$ and $\displaystyle\lim_{n \to \infty} w_n = b$ then the following all hold.
The proofs of these results are exactly the same as in the real case. $\square$
Let $z_n \in \C$ for all $n \in \N$ and write $z_n = x_n + iy_n$. Then $z_n$ converges if and only if $x_n$ and $y_n$ converge.
Suppose that $z_n \rightarrow z$ and write $z=x+iy$. Then \[ |x_n-x| \leq \sqrt{ |x_n-x|^2 + |y_n-y|^2} = |z_n-z| \rightarrow 0 \] as $n\to\infty$. Hence $x_n \rightarrow x$. A similar argument show that $y_n \rightarrow y$.
Conversely, suppose that $x_n$ converges to $a$ and $y_n$ converges to $b$. Then \[ \lim_{n \to \infty} z_n = \lim_{n \to \infty} x_n + i \lim_{n \to \infty} y_n = a + ib \] so that $z_n \rightarrow a+ib$. $\square$