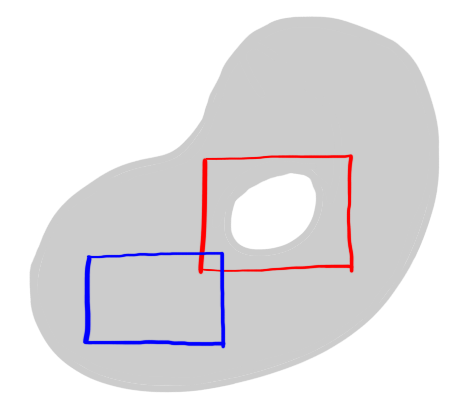
 it would be possible to apply the theorem to the blue rectangle, but it would not be possible to apply the theorem to the red rectangle.
it would be possible to apply the theorem to the blue rectangle, but it would not be possible to apply the theorem to the red rectangle.Home | Assessment | Notes | Index | Worksheets | Blackboard
There are many versions of Cauchy's theorem in complex analysis. They all give conditions under which the contour integral of a holomorphic function over a closed contour will be zero. Next week we will cover a sophisticated version whose condition is in terms of winding numbers. Here, we cover the most basic version: Cauchy's theorem in a rectangle.
Fix a domain $D \subset \C$ and $f : D \to \C$ holomorphic. For any rectangle $R$ which, together with its interior, is entirely contained within $D$ we have \[\int\limits_\gamma f(z) \intd z = 0\] where $\gamma$ is the contour parameterizing the edges of $R$ in turn.
Before we prove this theorem, there are two comments to make about its hypotheses.
 it would be possible to apply the theorem to the blue rectangle, but it would not be possible to apply the theorem to the red rectangle.
it would be possible to apply the theorem to the blue rectangle, but it would not be possible to apply the theorem to the red rectangle.We will also need the following lemma.
Fix $\gamma$ a smooth path in a domain $D$ and $f : D \to \C$ continuous. Then \[\left| \int\limits_\gamma f \right| \le \ell(\gamma) M\] where $M$ is any upper bound for $\{ |f(\gamma(t))| : a \le t \le b \}$.
Recall that the contour integral is a limit of Riemann sums \[\int\limits_\gamma f = \lim_{N \to \infty} \frac{b-a}{N} \sum_{n=1}^N f \left( \gamma \left( a + n \frac{b-a}{N} \right) \right) \gamma'\left( a + n \frac{b-a}{N} \right)\] so \[ \begin{aligned} \left| \int\limits_\gamma f \right| &= \lim_{N \to \infty} \frac{b-a}{N} \left| \sum_{n=1}^N f \left( \gamma \left( a + n \frac{b-a}{N} \right) \right) \gamma'\left( a + n \frac{b-a}{N} \right) \right| \\ & \le \lim_{N \to \infty} \frac{b-a}{N} \sum_{n=1}^N \left| f \left( \gamma \left( a + n \frac{b-a}{N} \right) \right) \gamma'\left( a + n \frac{b-a}{N} \right) \right| \\ & \le M \lim_{N \to \infty} \frac{b-a}{N} \sum_{n=1}^N \left| \gamma' \left( a + n \frac{b-a}{N} \right) \right| \\ & = M \int\limits_a^b |\gamma'(t)| \intd t = M \ell(\gamma) \end{aligned}\] as claimed. $\square$
Suppose that the integral is not zero. Write $\rho$ for the perimiter of $R$. Subdivide $R$ into four equally sized rectangles $R(1),R(2),R(3),R(4)$. We have \[\int\limits_{R(1)} f(z) \intd z + \int\limits_{R(2)} f(z) \intd z + \int\limits_{R(3)} f(z) \intd z + \int\limits_{R(4)} f(z) \intd z = \int\limits_R f(z) \intd z \] so there is a rectangle $S(1) \in \{R(1), R(2), R(3), R(4) \}$ with \[ \left| \int\limits_{S(1)} f(z) \intd z \right| \ge \frac{1}{4} \left| \int\limits_R f(z) \intd z \right| \] as otherwise the triangle inequality would give a contradiction. Repeating this argument, now subdividing $S(1)$ into four equal sub-rectangles, one of the sub-rectangles $S(2)$ will satisfy \[ \left| \int\limits_{S(2)} f(z) \intd z \right| \ge \frac{1}{4} \left| \int\limits_{S(1)} f(z) \intd z \right| \ge \frac{1}{4^2} \left| \int\limits_R f(z) \intd z \right| \] via the same argument as before. Continuing by induction, we get a sequence $S(n)$ of rectangles with
There is a unique point $\zeta$ contained in all of the rectangles $S(n)$. Fix \[\epsilon = \frac{1}{2\rho^2} \left| \int\limits_\gamma f(z) \intd z \right|\] and choose $r > 0$ such that \[\left| f(\zeta + h) - \left( f(\zeta) + h f'(\zeta) \right) \right| < |h| \epsilon\] holds whenever $|h| < r$. Fix $n$ so large that $S(n) \subset \ball(\zeta,r)$. Thus for every $z \in S(n)$ we have \[ \left| f(z) - \Big( f(\zeta) + (z - \zeta) f'(\zeta) \Big) \right| \le |z - \zeta| \epsilon \] and can estimate that \[ \begin{align*} & \left| \int\limits_{S(n)} \!\! f(z) \intd z \right| \\ ={} & \bigg| \int\limits_{S(n)} f(z) - \left( f(\zeta) + (z - \zeta) f'(\zeta) \right) \intd z \\ & \qquad + \int\limits_{S(n)} f(\zeta) + (z - \zeta) f'(\zeta) \intd z \bigg| \\ \le{} & \epsilon \int\limits_{S(n)} |z-\zeta| \intd z \le \frac{\epsilon \rho^2}{4^n} \end{align*} \] using the estimation lemma and the fact that \[g(z) = f(\zeta) + (z - \zeta) f'(\zeta)\] has an anti-derivative on $D$. Relating this to the original rectangle $R$ gives \[ \frac{\epsilon \rho^2}{4^n} \ge \left| \int\limits_{S(n)} f(z) \intd z \right| \ge \frac{1}{4^n} \left| \int\limits_R f(z) \intd z \right| \] and allows us to conclude that \[ \epsilon \rho^2 \ge \left| \int\limits_R f(z) \intd z \right| \] contradicting our choice of $\epsilon$. The original integral must therefore be zero. $\square$