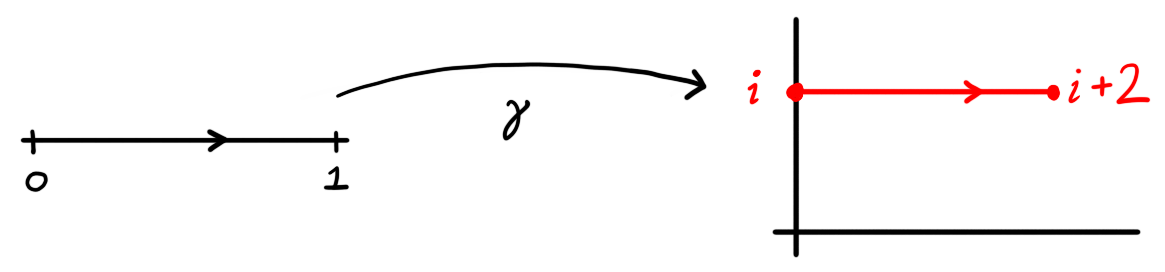
Figure 1: The image of the interval $[0,1]$ under the function $\gamma(t) = 2t + i$ describes route from $\gamma(0) = i$ to $\gamma(1) = 2+i$.
Home | Assessment | Notes | Index | Worksheets | Blackboard
Roughly speaking, a path will be a description of a journey in the complex plane. More formally, a path will be a parameterization of a continuous curve in the plane. In this section we make clear what is meant by this. We will be using paths throughout the course.
Fix $a \le b$ real. A path in $\C$ is any continuous function $\gamma : [a,b] \to \C$.
We will think of a path as describing the traversal of a curve in the complex plane from $\gamma(a)$ to $\gamma(b)$.
The function \[\gamma(t) = 2t + i = (1-t)i + t(i+2)\] defined on $[0,1]$ is a path. It describes a staight trajectory from $\gamma(0) = i$ to $\gamma(1) = 2 + i$.

Figure 1: The image of the interval $[0,1]$ under the function $\gamma(t) = 2t + i$ describes route from $\gamma(0) = i$ to $\gamma(1) = 2+i$.
The function \[\gamma(t) = 2 \cos(t) + 2 i \sin(t)\] defined on $[0,3 \pi / 2]$ is a path. It describes a circular trajectory from $\gamma(0) = 2$ to $\gamma(3 \pi /2) = -2i$.
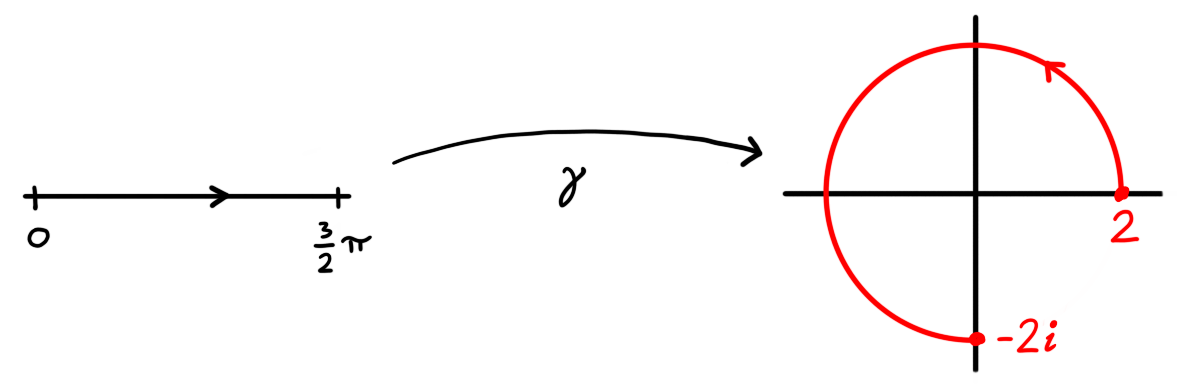
Figure 2: The image of the interval $[0,3 \pi / 2]$ under the function $\gamma(t) = 2 \cos(t) + 2 i \sin(t)$ describes a route from $\gamma(0) = 2$ to $\gamma(3 \pi / 2) = -2i$.
Informally, a path is continuous if its trajectory can be drawn without lifting the pen from the paper. The formal definition involves limits. We now discuss formally what we mean by continuity of a map from an interval to the complex plane.
Fix $a \le b $ real. A function $\gamma : [a,b] \to \C$ is continuous at $c \in [a,b]$ if \[\lim_{t \to c} \gamma(t) = \gamma(c)\] holds as a limit in the real sense. We say that $\gamma$ is continuous if it is continuous at every $a \le c \le b$.
When curves are given by simple formulae as in the previous example, we can use the laws of limits to determine whether they are continuous.
The function defined on $[1,2]$ by \[\gamma(t) = \begin{cases} i+t & t < 1.5 \\ 1 + it & t \ge 1.5 \end{cases}\] is not a path.
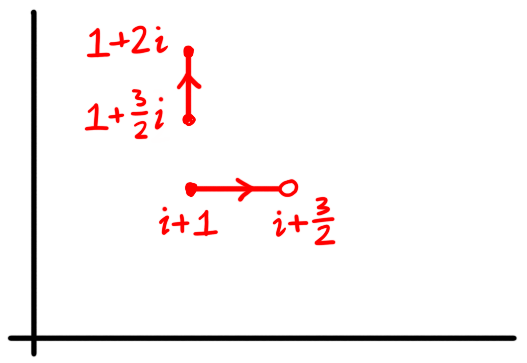
Figure 3: For $0 \le t < 1.5$ the function $\gamma$ traverses the horizontal segment and for $1.5 \le t \le 2$ it traverses the vertical segment. Since they are not joined together, we suspect $\gamma$ is not continuous.
To see this, we calculate the limits from the left and from the right as $t$ tends to $1.5$. We have \[ \begin{aligned} \lim_{t \to 1.5+} \gamma(t) & = \lim_{t \to 1.5+} 1 + it = 1 + \tfrac{3}{2} i \\ \lim_{t \to 1.5-} \gamma(t) & = \lim_{t \to 1.5-} i+t = \tfrac{3}{2} + i \end{aligned} \] and these limits are not the same, verifying what we suspect from the picture.