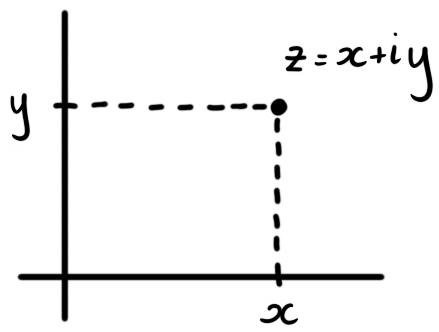
Figure 1: The complex number $z = x+iy$ reprenented as the point $(x,y)$ in the plane.
Home | Assessment | Notes | Index | Worksheets | Blackboard
We are familiar with the set $\R$ of real numbers. In earlier courses covering real analysis we learned about convergence of sequences of real numbers, continuity of functions defined on sets of real numbers, and the calculus of functions defined on subintervals of the real numbers.
This course is about the analysis of a different number system: the system $\C$ of complex numbers. When we learn about limits and continuity in the complex number system, the material will seem for the most part similar to what happens over the real number system. We will spend most of the course learning the calculus of the complex number system, which is distinct and powerful.
We begin the course with what complex numbers are and how we can picture them.
A complex number is an expression of the form \[x + iy\] where $x$ and $y$ are real numbers. We write $\C$ for the set of all complex numbers.
We usually use letters like $z$ and $w$ to represent complex numbers.
If $z = x+iy$ then $x$ is the real part of $z$ and $y$ is the imaginary part of $z$. Write $\Re(z)$ for the real part of $z$ and write $\Im(z)$ for the imaginary part of $z$.
Both the real and imaginary parts of a complex number are real!
We have defined a complex number to be an expression $x+iy$ where $x$ and $y$ are real. Strictly speaking $x+iy$ is merely a formal expression representing two real numbers $x$ and $y$ together. No meaning has yet been ascribed to the symbols $+$ and $i$ in the expression.
Thinking of $x+iy$ as two real numbers $x$ and $y$ suggests a geometric representation of $x+iy$ as the point $(x,y)$ in the plane. Representing complex numbers in this way came about in the 18th century, two hundred years after complex numbers first appeared.
Figure 1: The complex number $z = x+iy$ reprenented as the point $(x,y)$ in the plane.
We say that $z \in \C$ is real if $\Im(z)=0$ and we say that $z \in \C$ is imaginary if $\Re(z)=0$.
In the complex plane, the set of real numbers lie on the horizontal axis (which we will often call the real axis) and the set of imaginary numbers lie on the vertical axis (which we will often call the imaginary axis).
If we picture complex numbers as lying in the plane we can consider Euclidean properties of complex numbers. In particular, every non-zero complex is a certain distance from the origin that we can calculate using the Pythagoras theorem, and every non-zero complex makes an angle with the positive real axis that we can relate to other properties via trigonometry.
Figure 2: The line from the origin to $z = x + iy$ has length $\sqrt{x^2 + y^2}$ by Pythagoras.
The modulus or absolute value of the complex number $z$ is the quantity \[|z| = \sqrt{x^2 + y^2}\] measuring the distance between $z$ and the origin.
What is the modulus of $-4 + i3$?
We calculate that $|(-4) + i3| = \sqrt{(-4)^2 + 3^2} = 5$.
We conclude this section with the polar representaton of a complex number. When we plot $z = x + iy$ as a point in the plane the quantity $|z|$ is its distance from the origin. The angle $\theta$ from the positive real axis anti-clockwire to $z$ is called an argument of $z$.
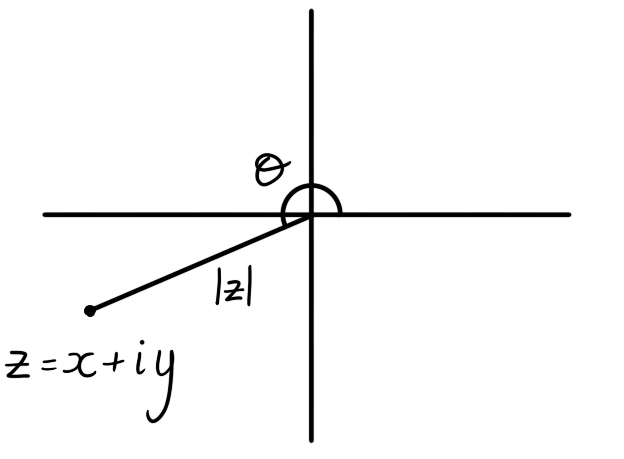
Figure 3: The complex number $z = x+iy$ makes a counter-clockwise angle $\theta$ with the positive real axis.
We say "an argument" because it is not uniquely determined: if we replace $\theta$ by $\theta + 2f n \pi$ for any $n \in \Z$ then we describe the same complex number. However, there is always a unique argument $-\pi < \theta \le \pi$.
The principle argument of a non-zero complex number $z$ is the value \[-\pi < \Arg(z) \le \pi\] representing the anti-clockwise angle between $z$ and the positive real axis.
Although every non-zero complex number has many arguments, each non-zero complex number has only one principle argument.
Fix $z \in \C$ non-zero. Writing $r = |z|$ and $\theta = \Arg(z)$ we call \[z = r \left( \cos(\theta) + i \sin(\theta) \right)\] the polar representation of $z$.
Write the polar representation of $z = \sqrt{3} - i$.
The modulus of $\sqrt{3} - i$ is $2$.
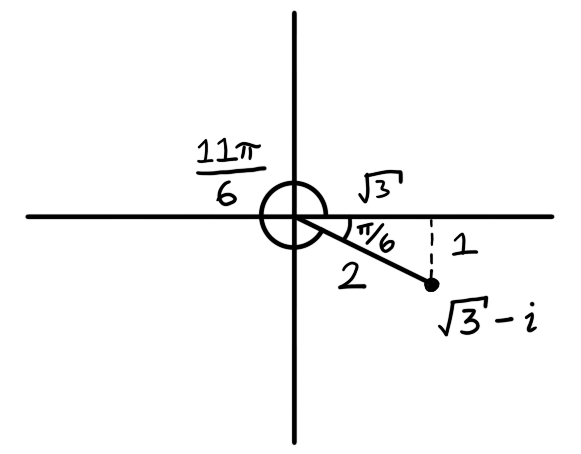
There is an angle of $\pi/6$ between $z$ and the positive real axis. This is not an argument of $z$ as it a clockwise measurement. $11 \pi /6$ is an argument of $z$ but not its principle argument as it is not in the range $- \pi < \theta \le \pi$. The principle argument of $z$ is $-\pi/6$ and \[ 2(\cos(-\pi/6) + i \sin(- \pi / 6)) \] is the polar representation of $z$.