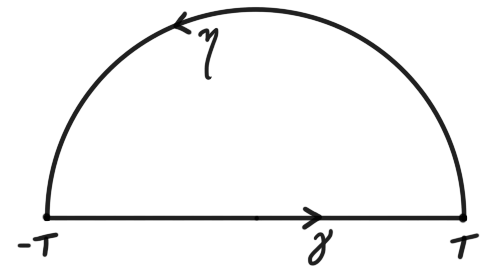
Figure 1: The contour $\Gamma = (\gamma,\eta)$ used to calculate infinite real integrals using Cauchy's residue theorem.
Home | Assessment | Notes | Index | Worksheets | Blackboard
In this section we will use Cauchy's residue theorem to calculate integrals of the form \[ \int\limits_{-\infty}^\infty f(t) \intd t \] where $f : \R \to \R$ decays suitably at infinity. Generally, the above notation is shorthand for the limit \[ \lim_{A,B \to \infty} \int\limits_{-A}^B f(t) \intd t \] but in this course we will only consider the special case covered by the following lemma.
Fix $f : \R \to \R$ continuous. If there is $C > 0$ and $r > 1$ with $|f(t)| \le C / |t|^r$ for all $t \in \R$ then \[ \int\limits_{-\infty}^\infty f(t) \intd t \] exists and equals \[ \lim_{T \to \infty} \int\limits_{-T}^T f(t) \intd t \] exists.
Fix $0 < S < T$ and calculate \[ \begin{aligned} \left| \int\limits_{-T}^T f(t) \intd t - \int\limits_{-S}^S f(t) \intd t \right| & = \left| \int\limits_{-T}^{-S} f(t) \intd t + \int\limits_S^T f(t) \intd t \right| \\ & \le \int\limits_{-T}^{-S} \dfrac{C}{|t|^r} \intd t + \int\limits_S^T \dfrac{C}{|t|^r} \intd t \\ & = 2C \int\limits_S^T \dfrac{1}{t^r} \intd t \\ & = \dfrac{2C}{1-r} \left[ \dfrac{1}{t^{r-1}} \right]_S^T = \dfrac{2C}{r-1} \left( \dfrac{1}{S^{r-1}} - \dfrac{1}{T^{r-1}} \right) \end{aligned} \] which will be at most $\epsilon$ whenever $S,T$ are large enough. This imples that, as $T \to \infty$, the quantity \[ \int\limits_{-T}^T f(t) \intd t \] is Cauchy and therefore converges. A similar line of argument proves the second part of the lemma. $\square$
The connection between infinite real integrals and contour integration is given by the contour $\Gamma = (\gamma,\eta)$ where $\gamma(t) = t$ on $[-T,T]$ and $\eta(t) = Te^{it}$ on $[0,\pi]$. Indeed - provided one can extend the definition of $f$ to a domain containing $\R$ - one has \[ \int\limits_\Gamma f = \int\limits_\gamma f + \int\limits_\eta f = \int\limits_{-T}^T f(t) \intd t + \int\limits_0^\pi f(Te^{it}) i T e^{it} \intd t \] and we are faced with two tasks.
The first involves the calculation of any residues $f$ may have inside $\Gamma$. For the second we need $f$ to decay as $T \to \infty$ in some way.

Figure 1: The contour $\Gamma = (\gamma,\eta)$ used to calculate infinite real integrals using Cauchy's residue theorem.
Lets evaluate \[\int\limits_{-\infty}^\infty \dfrac{1}{(t^2+1)(t^2+4)} \intd t\] using the above approach. First, we estimate that \[ \left| \dfrac{1}{(t^2+1)(t^2+4)} \right| \le \dfrac{1}{t^4} \] for all $t \in \R$ so that the lemma applies, allowing us to follow the strategy outlined above. Define $f$ on $\C \setminus \{i,-i,2i,-2i\}$ by \[ f(z) = \dfrac{1}{(z^2 + 1)(z^2 + 4)} \] and put $\eta(t) = Te^{it}$ on $[0,\pi]$. We can estimate \[ \left| \int\limits_0^\pi f(Te^{it}) i T e^{it} \intd t \right| \] if we have an upper bound for $|f(T e^{it})|$ on $[0,\pi]$. But \[ |f(z)| = \dfrac{1}{|z-i| |z+i| |z-2i| |z+2i| } \le \dfrac{1}{(|z| - 1)^2 (|z| - 2)^2} \] using the reverse triangle inequality, so \[ |f(Te^{it})| \le \dfrac{1}{(T - 1)^2 (T - 2)^2} \le \dfrac{100}{T^4} \] for all $T$ large enough. We conclude that \[ \left| \int\limits_0^\pi f(Te^{it}) i T e^{it} \intd t \right| \le \int\limits_0^\pi \dfrac{100}{T^4} T \intd t \le \dfrac{2 \pi}{T^3} \] so that the contour integral over $\eta$ goes to zero as $T \to \infty$. When $T$ is large $\Gamma$ contains $i$ and $2i$ so \[ \int\limits_{-\infty}^\infty \dfrac{1}{t^2 + 1}{t^2 + 4} \intd t = 2 \pi i \Res(f,i) + 2 \pi i \Res(f,2i) \] by Cauchy's residue theorem. The residues are \[ \begin{aligned} \Res(f,i) & = \lim_{z \to i} \dfrac{z-i}{(z^2 + 1)(z^2 + 4)} = \dfrac{1}{6i} \\ \Res(f,2i) & = \lim_{z \to 2i} \dfrac{z-2i}{(z^2 + 1)(z^2 + 4)} = - \dfrac{1}{12 i} \end{aligned} \] so \[\int\limits_{-\infty}^\infty \dfrac{1}{(t^2+1)(t^2 + 4)} \intd t = \dfrac{\pi}{3} - \dfrac{\pi}{6} = \dfrac{\pi}{6}\] concluding the example.