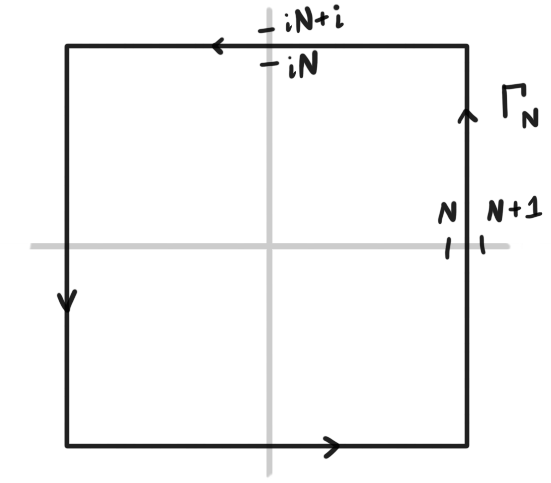
Figure 1: The square contour $\Gamma_N$ contains the poles of $g$ at $-N,\dots,N$ and possibly poles of $f$ as well.
Home | Assessment | Notes | Index | Worksheets | Blackboard
We can also use Cauchy's residue theorem to sum series. The link between the two is the function $g(z) = \cot(\pi z)$ which we define on $\C \setminus \Z$ by $g(z) = \cos(\pi z) / \sin(\pi z)$. Since $\sin(\pi z)$ has a simple zeroe at every integer and $\cos(\pi z)$ is non-zero at every integer our function $g$ has a simple pole at every integer. It also has no other poles. We can calculate that \[ \Res(g,n) = \dfrac{\cos(\pi n)}{\pi \cos(n \pi)} = \dfrac{1}{\pi} \] using our lemma for residues of simple poles of ratios.
Suppose now that we are given a series \[\sum_{n=1}^\infty a_n\] that we wish to sum. Suppose that the terms $a_n$ are all non-zero and that we can find a meromorphic function $f : \C \to \C$ with $f(n) = a_n$ for all $n \in \N$. We can calculate that \[ \Res(fg,n) = \dfrac{f(n) \cos(\pi n)}{\pi \cos(\pi n)} = \dfrac{f(n)}{\pi} = \dfrac{a_n}{\pi} \] so that \[ 2 i \sum_{n=1}^N a_n = 2 \pi i \sum_{n=1}^N \Res(fg,n) \] will contribute to the conclusion of Cauchy's residue theorem whenever $\Gamma$ is a contour with a winding number of $1$ around each of $1,\dots,N$. Depending on what other poles $f$ has - and we will see some examples later - there may be other contributions as well.
The contour $\Gamma_N$ we will use will be a square centered at the origin with sides parallel to the axes and of length $2N + 1$. We want the contour integral to vanish as $N \to \infty$ leaving only the residues of $g$ that give the series, and the additional residues of $f$ that will tell us the value of the series.

Figure 1: The square contour $\Gamma_N$ contains the poles of $g$ at $-N,\dots,N$ and possibly poles of $f$ as well.
For the contour integral to vanish as $N \to \infty$ we will need to estimate the integral \[ \int\limits_{\Gamma_N} f(z) \cot(\pi z) \intd z \] as $N \to \infty$. As we will see in the example, the following lemma tells us that strong enough decay in $|f(z)|$ as $|z| \to \infty$ will suffice.
There is $M > 0$ such that $|\cot(\pi z)| \le M$ whenever $N \in \N$ and $z$ lies on $\Gamma_N$.
Calculate \[\sum_{n=1}^\infty \dfrac{1}{n^2}\] using the lemma and the strategy above.
Take $f(z) = 1/z^2$ on $\C \setminus \{0\}$ so that $f(\pm n) = 1/n^2$ for all $n \in \N$. For every non-zero $n \in \Z$ we have \[ \Res(fg,n) = \dfrac{1}{n^2 \pi} \] as above. At $-n$ we have the same residue. Thus \[ \int\limits_{\Gamma_N} \dfrac{1}{z^2} \dfrac{\cos(\pi z)}{\sin(\pi z)} \intd z = 4 \pi i \sum_{n=1}^N \dfrac{1}{n^2 \pi} + 2 \pi i \Res(fg,0) \] and it remains to both dispense with the contour integral and calculate the reimaining residue.
For the contour integral, note that \[ \left| \int\limits_{\Gamma_N} \dfrac{1}{z^2} \cot(\pi z) \intd z \right| \le \ell(\Gamma_N) \dfrac{M}{N^2} = M \dfrac{4(2N+1)}{N^2} \] from our lemma on the cotangent function and the fact that $|z| \ge N$ for all $z$ on $\Gamma_N$. This quantity goes to zero as $N \to \infty$ so \[ 0 = 4 \pi i \sum_{n \in \N} \dfrac{1}{n^2 \pi} + 2 \pi i \Res(fg,0) \] and it remains to calculate the residue at the origin.
The pole at the origin has order three. The residue is therefore \[ \lim_{z \to 0} \dfrac{1}{2} \left( \dfrac{z^3 \cos(\pi z)}{z^2 \sin(\pi z)} \right)^{(2)} \] and \[ \dfrac{z}{\sin z} = 1 + \dfrac{z^2}{6} + \cdots \] so \[ \dfrac{z}{\sin(\pi z)} = \dfrac{1}{\pi} \dfrac{\pi z}{\sin(\pi z)} = \dfrac{1}{\pi} \left( 1 + \dfrac{\pi^2 z^2}{6} + \cdots \right) \] and \[ \begin{align*} & \dfrac{z}{\sin(\pi z)} \cos(\pi z) \\ ={} & \dfrac{1}{\pi} \left( 1 + \dfrac{\pi^2 z^2}{6} + \cdots \right) \left( 1 - \dfrac{\pi^2 z^2}{2!} + \cdots \right) \\ ={} & = \dfrac{1}{\pi} - \dfrac{\pi}{3} z^2 + \cdots \end{align*} \] so that $\Res(fg,0) = -\pi/3$. Plugging into what we had earlier gives \[\sum_{n=1}^\infty \dfrac{1}{n^2} = \dfrac{\pi^2}{6}\] concluding the example.