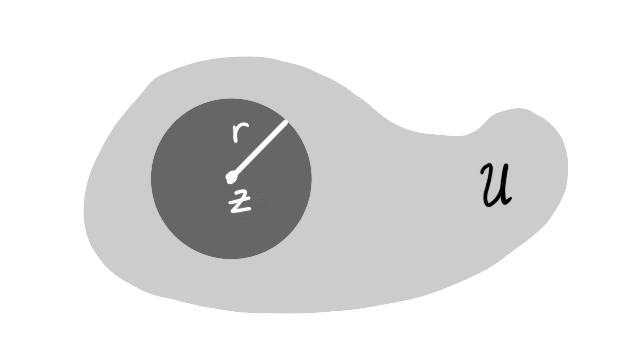
Figure 1: In this example the open ball of radius $r$ centered at $z$ is entirely contained within the shaded set $U$.
Home | Assessment | Notes | Index | Worksheets | Blackboard
In real analysis, one normally studies real-valued functions $f$ defined on open intervals $(a,b)$, $(-\infty,b)$, $(a,\infty)$ or $(-\infty,\infty)$. These are the natural subsets of $\R$ on which to first define differentiation and integration. This is because, when studying whether a function $f : (a,b) \to \R$ is differentiable at a point $a$ we want to be able to look at points $x$ near to $a$ i.e. either slightly to the left or slightly to the right of $a$ and to take limits as $x \to a$; and because when integrating we don't want their to be any gaps in the domain of our function. Formally, the intervals above are the only subsets of $\R$ that are open and path connected.
In this section we will make the terms open and path connected precise in the complex plane. It will turn out that open and path connected subsets of $\C$ are much more varied topologically than in the real case. This is one of the main reasons that complex analysis in one variable is so much more interesting than real analysis in one variable.
We will first discuss open subsets of $\C$. Recall from the previous section that the open ball centered at $z \in \C$ of radius $r > 0$ is the set $\ball(z,r) = \{ w \in \C : |z-w| < r \}$.
A set $U \subset \C$ is open if, for every $z \in U$ there is $r > 0$ such that $\ball(z,u) \subset D$.

Figure 1: In this example the open ball of radius $r$ centered at $z$ is entirely contained within the shaded set $U$.
For every $z \in \C$ and every $r > 0$ the open ball $\ball(z,r)$ is open.
Fix $w \in \ball(z,r)$. We need to find $s > 0$ such that $\ball(w,s) \subset \ball(z,r)$. Choose $s = r - |z-w|$. Fix $u \in \ball(w,s)$. This means $|w-u| < s$. We need to prove that $u \in \ball(z,r)$. We estimate \[|u-z| < |u-w| + |w-z| < r - |z-w| + |w-z| = r\] using the triangle inequality, giving the desired inclusion. $\square$
The set \[E = \{z \in \C : \Im(z) = 0 \}\] is not open. Indeed, there is no open ball centered at $1$ entirely contained within $E$. This is because every open ball centered at $1$ contains $1+is$ for some $s > 0$.
A set $E \subset \C$ is said to be closed its its complement $\C \setminus E$ is open.
Note that a set is closed precisely when the complement is open. A very common mistake is to think that "closed" means "not open"! Unlike in real life, here this is not the case, and it is easy to write down examples of sets that are neither open nor closed, and examples of sets that are both open and closed!
Now lets discuss path connected sets.
A set $Q \subset \C$ is path connected if for any two points $z,w \in Q$ there is a path $\gamma : [0,1] \to Q$ with $\gamma(0) = z$ and $\gamma(1) = w$.
Recall from the previous section that, informally, a path is continuous if its trajectory can be drawn without lifting the pen from the paper. We therefore think (informally!) of a set $Q \subset \C$ being path connected if you are able to draw a curve from any point of $Q$ to any other point of $Q$ without ever drawing outside $Q$ or lifting your pen from the paper. In this course, we will almost always work with sets whose path connectedness can easily be determined by visual inspection.
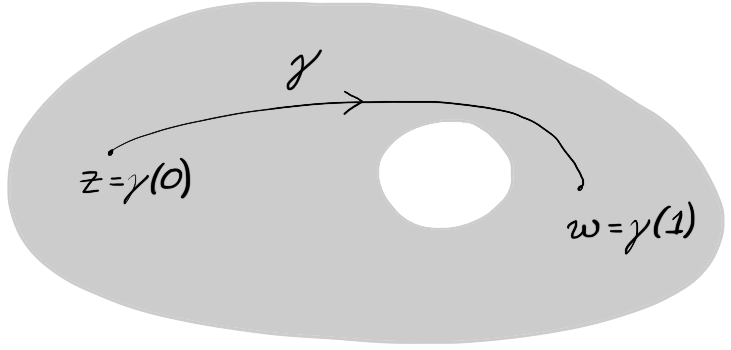
Figure 3: The trajectory of a path $\gamma$ connecting $z$ to $w$ and staying entirely within the shaded set $Q$.
For every $z \in \C$ and every $r > 0$ the open ball $\ball(z,r)$ is path connected.
Fix $w \in \ball(z,r)$. Define $\gamma$ on $[0,1]$ by $\gamma(t) = (1-t)z + tw$. Certainly $\gamma$ is continuous and $\gamma(t) \in \ball(z,r)$ for all $0 \le t \le 1$. Since $\gamma(0) = z$ and $\gamma(1) = w$ we have formed a continuous path from $z$ to an arbitrary point $w$ in our set. It $u$ is any other point in $\ball(z,r)$ we can get a continuous path from $u$ to $w$ by first traversing backwards the path from $z$ to $u$, and then traversing forwards the path from $z$ to $w$. Thus $\ball(z,r)$ is path connected. $\square$
If a set is made up of two disjoint open pieces then it will not be path connected.
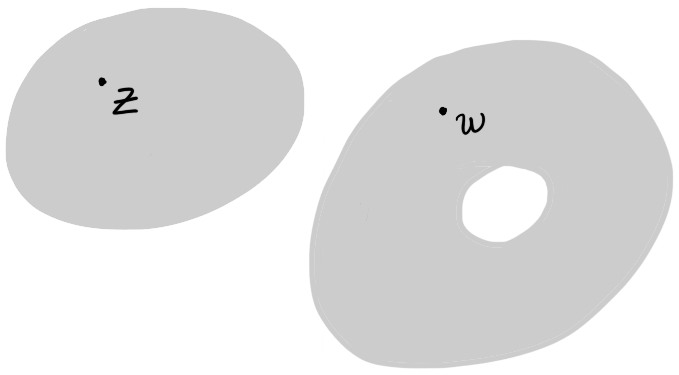
Figure 4: There is no path between $z$ and $w$ that stays entirely within the shaded set shown, because any continuous map $\gamma : [0,1] \to \C$ with $\gamma(0) = z$ and $\gamma(1) = w$ must pass through the dashed line, which is not within the shaded region.
A set $D \subset \C$ is a domain if it is non-empty, open and path connected.
Throughout the course we will be working with domains. We will think of them as being analogous to subintervals of the line..
Here are some examples and non-exmaples of domains.