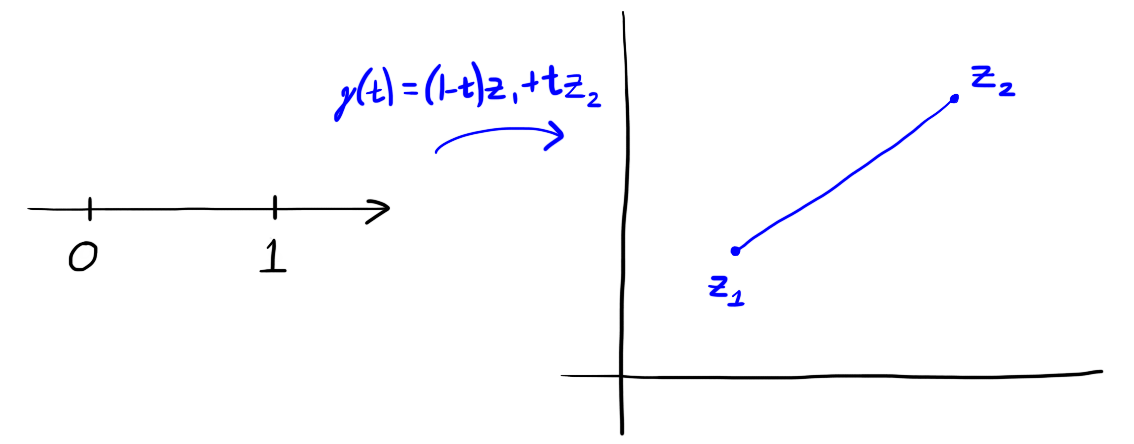
Figure 1: The path $\gamma(t) = (1-t)z_1 + tz_2$ on $[0,1]$ is a straight line from $z_1$ to $z_2$.
Home | Assessment | Notes | Index | Worksheets | Blackboard
Recall that a path in $\mathbb{C}$ is any continuous function $\gamma : [a,b] \to \mathbb{C}$. We met paths in Week 2 when we discussed continuous functions. We will think of a path as describing a specific way of travelling from $\gamma(a)$ to $\gamma(b)$ in the complex plane. We will typically deal with simple paths like straight lines and circular arcs.
For any two complex numbers $z_1,z_2$ the straight-line from $z_1$ to $z_2$ can be parameterized by $\gamma : [0,1] \to \C$ with $\gamma(t) = (1-t)z_1 + t z_2$.
Figure 1: The path $\gamma(t) = (1-t)z_1 + tz_2$ on $[0,1]$ is a straight line from $z_1$ to $z_2$.
For any complex numbers $w$ and any $r > 0$ the circular path centered at $w$ of radius $r$ can be parameterized by $\gamma : [0,2\pi] \to \C$ with $\gamma(t) = w + r \exp(i t)$.
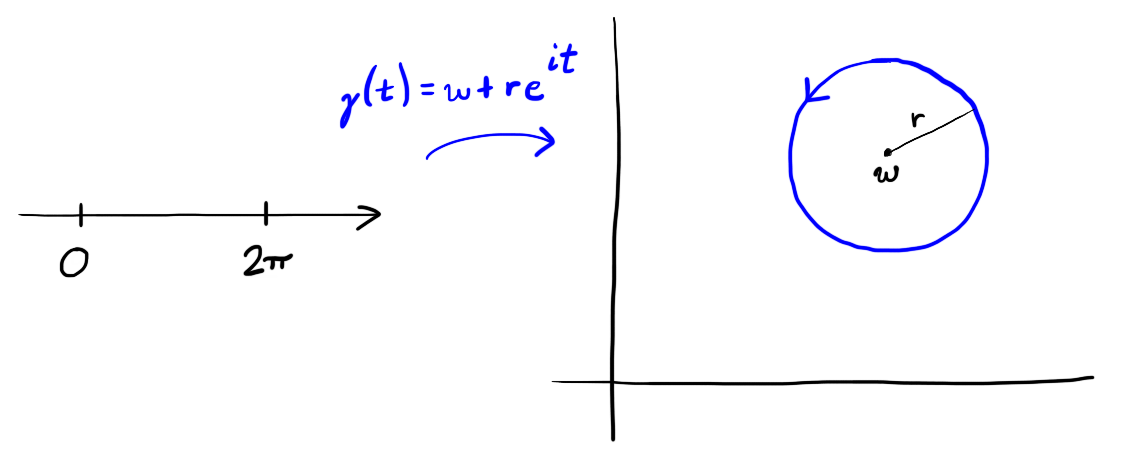
Figure 2: The path $\gamma(t) = w + r \exp(it)$ on $[0,2\pi]$ is a circular path around $w$ starting at $w + r$.
A path $\gamma : [a,b] \to \C$ is closed if $\gamma(b) = \gamma(a)$.
We will be using paths to define integrals. Not all paths are suited for this purpose. In this course we will work with smooth paths.
A smooth path is a path $\gamma$ with the property that its derivative \[\gamma'(t) = \lim_{h \to 0} \frac{\gamma(t+h) - \gamma(t)}{t}\] exists for every $t \in [a,b]$ and $\gamma'$ is continuous on $[a,b]$.
Roughly speaking, a path is smooth if it has a continuously varying tangent line at every point. Thus smooth paths cannot have cusps or sharp corners.
Figure 3: A smooth path has a tangent line at every point $\gamma(t)$.
In a more advanced course we would work with the broader class of rectifiable curves. Rectifiability is a property that, amongst other things, guarantees that a path has a well-defined length. For smooth paths, we can define length by a formula.
The length of a smooth path $\gamma : [a,b] \to \C$ is \[\int\limits_a^b |\gamma'(t)| \intd t\] which is denoted $\ell(\gamma)$.
Note that $|\gamma'(t)|$ is a real number so the integral defining the length does not involve complex analysis. It is a Riemann integral and can be calculated using techniques from Calculus.
Calculate the lengths of the following smooth paths.
We calculate as follows.
Often we will want to integrate over a number of paths joined together. One could make the latter a path by constructing a suitable reparametrisation, but in practice this makes things complicated; in particular the joins may not be smooth. It is simpler to give a name to several smooth paths joined together.
A contour is a finite list $(\gamma_1,\dots,\gamma_n)$ of smooth paths with the property that $\gamma_{i+1}$ starts where $\gamma_i$ ends for every $1 \le i \le n-1$.
We usually write $\Gamma = (\gamma_1,\dots,\gamma_n)$ for a contour.
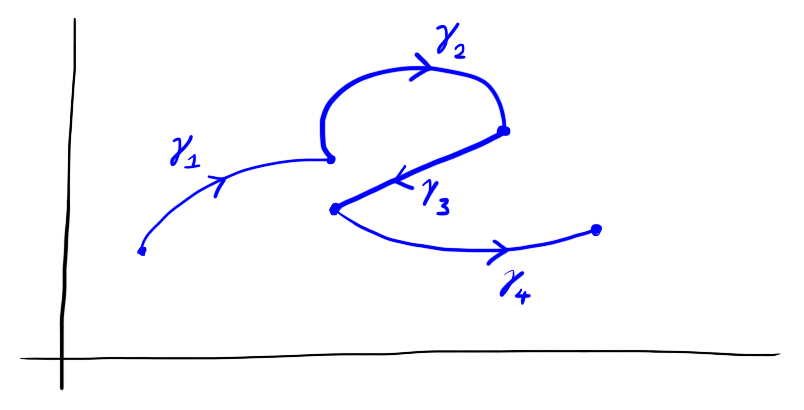
Figure 4: A contour consists of a sequence paths, with successive paths beginning where preceding paths ended.
A contour $\Gamma = (\gamma_1,\dots,\gamma_n)$ is closed if $\gamma_n$ ends where $\gamma_1$ begins.
If $\Gamma = (\gamma_1,\dots,\gamma_n)$ is a contour then each of the $\gamma_i$ is a smooth path with a length $\ell(\gamma_i)$. It is then natural to define the length of a contour as follows.
The length of a contour $\Gamma = (\gamma_1,\dots,\gamma_n)$ is the sum \[\ell(\Gamma) = \ell(\gamma_1) + \cdots + \ell(\gamma_n)\] of the lengths of its constituent paths.
Define $\gamma_1 : [0,1] \to \C$ by $\gamma_1(t) = 2t-1$ and $\gamma_2 : [0,\pi] \to \C$ by $\gamma_2(t) = e^{it}$. The contour $(\gamma_1,\gamma_2)$ is a semicircle.
Its length is \[\int\limits_0^1 |\gamma_1'(t)| \intd t + \int\limits_0^\pi |\gamma_2'(t)| \intd t = \int\limits_0^1 2 \intd t + \int\limits_0^\pi |i e^{it}| \intd t = 2 + \pi \]