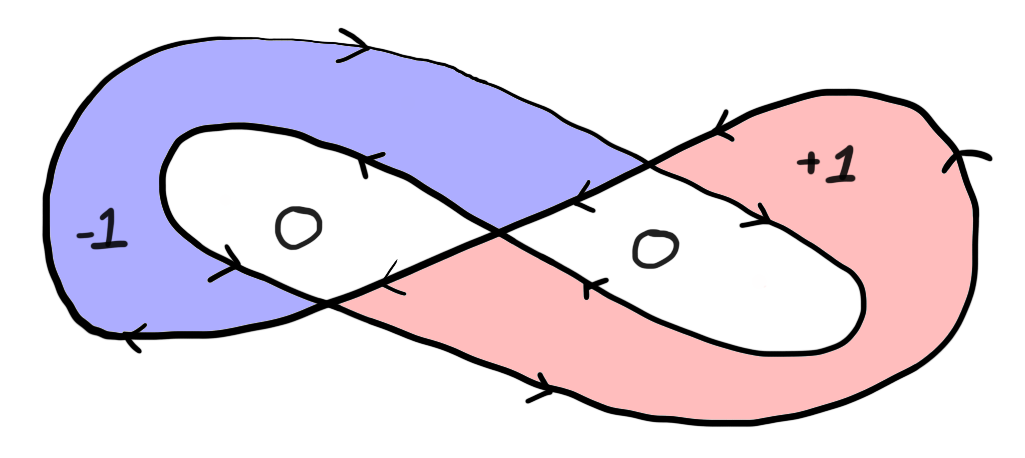
Figure 1: The winding number of the coutour around some points that appear inside the contour is zero.
Home | Assessment | Notes | Index | Worksheets | Blackboard
Generally, a contour in a domain can be quite complicated, interacting in a delicate way with the holes in the domain. From the last section, the winding number can tell us whether a contour "really" wraps around a hole in a domain. If $\wind(\gamma,z) = 0$ then $\gamma$ does not wrap around $z$ and we think of $z$ as being outside $\gamma$. Sometimes this can be a bit unintuitive.

Figure 1: The winding number of the coutour around some points that appear inside the contour is zero.
Thy hypothesis of our second version of Cauchy's theorem is in terms of winding numbers. It states that, given $f : D \to \C$ holomorphic and $\gamma$ a closed contour in $D$, the contour integral of $f$ over $\gamma$ will be zero whenever $\gamma$ does not wind around any points outwith $D$. Since $f$ is holomorphic on $D$ this assumption avoids the possibility of $\gamma$ winding around points where $f$ is not differentiable.
Fix a domain $D \subset \C$ and $f : D \to \C$ holomorphic. If $\Gamma$ is a closed contour in $D$ with $\wind(\Gamma,z) = 0$ for all $z \in \C \setminus D$ then $\displaystyle \int\limits_\Gamma f = 0$.
Here are some example contours and domains to help understand the hypothesis.
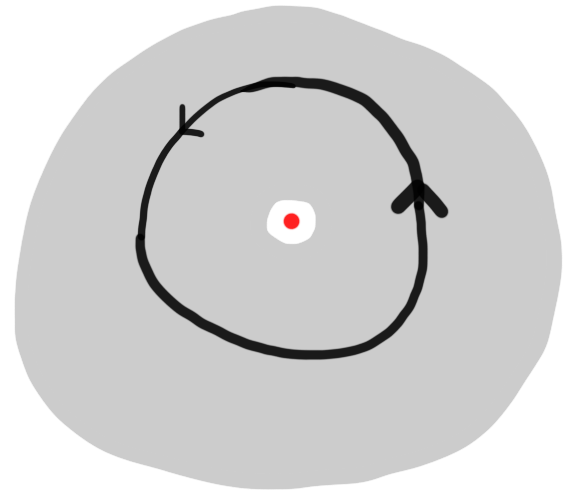
Figure 2: We may not apply Cauchy's theorem to holomorphic functions on the shaded domain $D$ because the contour $\Gamma$ winds around points (e.g. the red point) outside the domain.
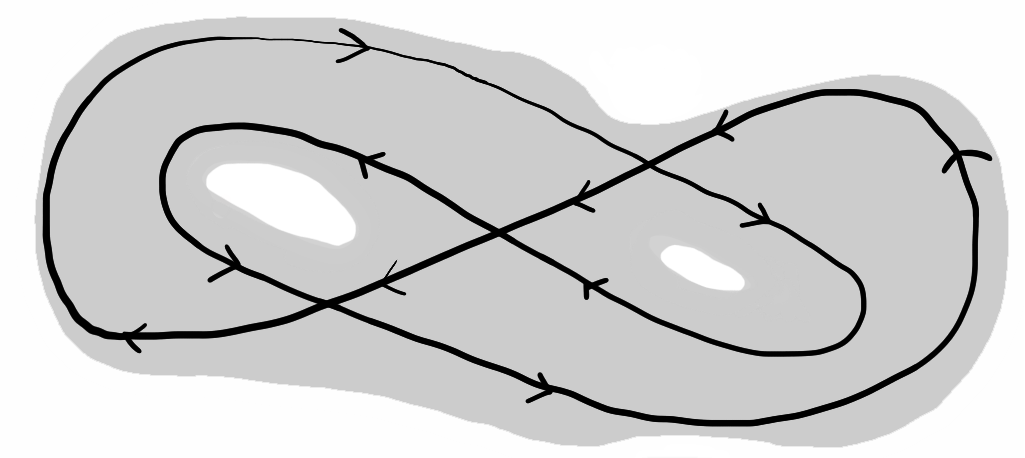
Figure 3: We may apply Cauchy's theorem to holomorphic functions on the shaded domain $D$ because the contour $\Gamma$ does not wind around any point outside the domain.
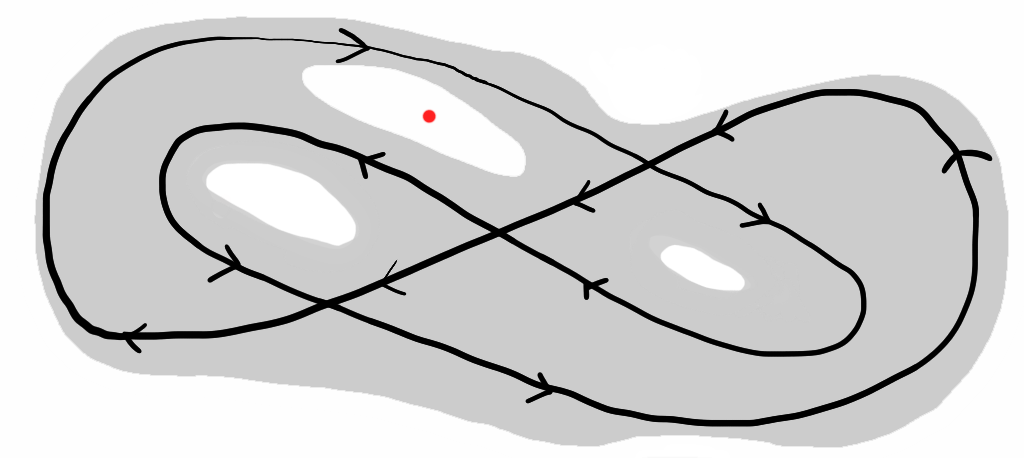
Figure 4: We may not apply Cauchy's theorem to holomorphic functions on the shaded domain $D$ because the contour $\Gamma$ winds around points (e.g. the red point) outside the domain.
A domain $D \subset \C$ is simply connected if for every closed contour $\Gamma$ in $D$ and every $z \notin D$ we have $\wind(\Gamma,z) = 0$.
Roughly speaking, a simply connected domain cannot have any holes in it: if a domain has a hole in it then we can find a contour that winds around it once.
Fix a domain $D \subset \C$. If $D$ is simply connected then \[\int\limits_\Gamma f = 0\] for every closed contour $\Gamma$ in $D$ and every holomorphic function $f : D \to \C$.
There is one more version of Cauchy's theorem we will mention.
Fix a domain $D \subset \C$ and $f : D \to \C$ holomorphic. If $\Gamma_1,\dots,\Gamma_m$ are closed contours in $D$ with \[ \wind(\Gamma_1,z) + \cdots + \wind(\Gamma_m,z) = 0 \] for all $z \in \C \setminus D$ then $\displaystyle\int\limits_{\Gamma_1} f + \cdots + \int\limits_{\Gamma_m} f = 0$
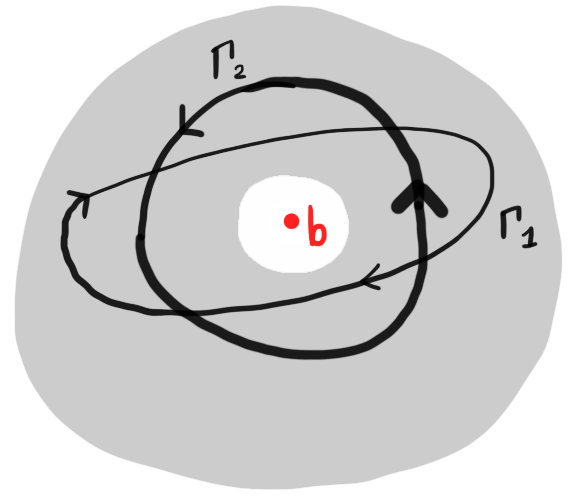
Figure 6: We may apply Cauchy's theorem to holomorphic functions on the shaded domain $D$ because the contours $\Gamma_1,\Gamma_2$ satisfy $\wind(\Gamma_1,b) + \wind(\Gamma_2,b) = 0$. This is despite the fact that both contours individually do wind around $b$.
We will not prove Cauchy's theorem in this course. When a domain is simply connected, one can imagine flooding a closed contour in $D$ with rectangles and applying Cauchy's theorem in a rectangle to each one.