Model-free estimation of a psychometric function

Home	Downloads	Demonstration	Documentation	Examples	Functions	Contacts

Example 1. Frequency of seeing

Miranda, M. A. & Henson, D. B. “Perimetric sensitivity and response variability in glaucoma with single-stimulus automated perimetry and multiple-stimulus perimetry with verbal feedback”, Acta Ophthalmologica, 86, 202-206, 2008.

MatLab R

Back to Examples

A flash of light of variable intensity was presented repeatedly at a fixed location in the visual field of a subject who reported whether the flash was visible. There were 3–20 trials at each stimulus level.

Load data

data("Miranda_Henson") x = Miranda_Henson$x r = Miranda_Henson$r m = Miranda_Henson$m

Loaded R data consist of three columns:

Stimulus level, x

Number of successes, r

Number of trials, m

Parametric fitting
Four different parametric models are fitted to these data: Gaussian (probit), Weibull, reverse Weibull and logistic. The parameters of the models are estimated in the Matlab functions binomfit_lims for the probit and logit links. The other two models require an estimate of the exponent K and the estimation is performed in the functions binom_weib and binom_revweib. The values of the fitted functions at specified points are calculated in the function binomval_lims.

First plot the psychometric data (black dots):

plot( x, r / m, xlim = c( 0.1, 1.302 ), ylim = c( 0.0165, 0.965 ), type = "p", pch="*" ) # Limits set to match the MatLab ones

1. For the Gaussian cumulative distribution function (black curve):

val <- binomfit_lims( r, m, x, link = "probit" ) # Plot the fitted curve numxfit <- 999 # Number of points to be generated minus 1 xfit <- (max(x)-min(x)) * (0:numxfit) / numxfit + min(x) pfit <- predict( val$fit, data.frame( x = xfit ), type = "response" ) lines(xfit, pfit )

2. For the Weibull function (red curve):

val <- binom_weib( r, m, x ) # Plot the fitted curve pfit <- predict( val$fit, data.frame( x = xfit ), type = "response" ) lines(xfit, pfit, col = "red" )

3. For the reverse Weibull function (green curve):

val <- binom_revweib( r, m, x ) # Plot the fitted curve pfit <- predict( val$fit, data.frame( x = xfit ), type = "response" ) lines(xfit, pfit, col = "green" )

4. For the logistic function (blue curve):

val <- binomfit_lims( r, m, x, link = "logit" ) # Plot the fitted curve pfit<-predict( val$fit, data.frame( x = xfit ), type = "response" ) lines(xfit, pfit, col = "blue" )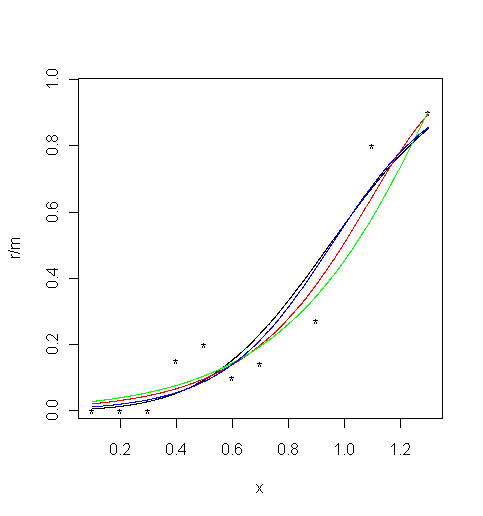

Local linear fitting

Local linear fitting is performed in the function locglmfit, which returns the fitted values at specified points. This function requires a bandwidth as an input. The bandwidth bwd is typically chosen by a cross-validation. There are three different loss functions used in cross-validation: ISE defined on a p-scale, ISE defined on an eta-scale, and deviance.

bwd_min <- min( diff( x ) ) bwd_max <- max( x ) - min( x ) bwd <- bandwidth_cross_validation( r, m, x, c( bwd_min, bwd_max ) )

The values of cross-validation bandwidths are

bwd = 0.1007 for ISE on a p-scale,

bwd = 0.2999 for ISE defined on an eta-scale,

bwd = 0.2959 for deviance.

Here, the bandwidth obtained with cross-validated deviance is used.

bwd <- bwd$deviance # Choose the estimate based on cross-validated deviance pfit <- locglmfit( xfit, r, m, x, bwd )$pfit plot( x, r / m, xlim = c( 0.1, 1.302 ), ylim = c( 0.0165, 0.965 ), type = "p", pch="*" ) # Limits set to match the MatLab ones lines(xfit, pfit )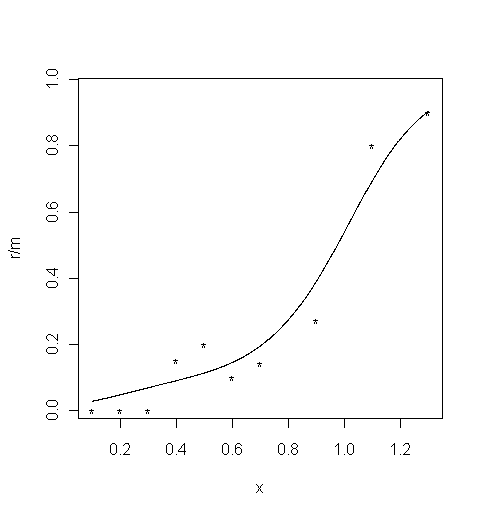

From the fitted values of the psychometric function, the threshold and slope for a requied threshold level, here prob = 0.5, are calculated in the function threshold_slope. The functions bootstrap_sd_th and bootstrap_sd_sl estimate their standard deviations by the percentile bootstrap method. In the following example, 200 bootstrap replications were used. Note that these functions, as with all bootstrap methods, return similar but slightly different values at each execution.

prob <- 0.5 # Required threshold level niter <- 200 # Number of bootstrap iterations thr_sl <- threshold_slope( pfit, xfit, prob ) sd_th <- bootstrap_sd_th( prob, r, m, x, niter, bwd ) # Be patient, slow process sd_sl <- bootstrap_sd_sl( prob, r, m, x, niter, bwd ) # Be patient, slow process

Examples of values returned by R are as follows:

threshold (sd_th) = 0.9745 (0.0558)

slope (sd_sl) = 1.5536 (0.2941)

Bootstrap estimates of confidence intervals for the threshold and slope are calculated by the functions bootstrap_ci_th and bootstrap_ci_sl; here a significance level alpha = 0.05 was used. Again, the these functions return similar but slightly different values at each execution.

prob <- 0.5 # Required threshold level alpha <- 0.05 # Significance level for the confidence intervals niterci <- 1000 # Number of bootstrap iterations ci_th <- bootstrap_ci_th( prob, r, m, x, niterci, bwd, alpha ) # Be patient, slow process ci_sl <- bootstrap_ci_sl( prob, r, m, x, niterci, bwd, alpha ) # Be patient, slow process

Examples of confidence intervals returned by R are as follows:

ci_th = [0.8363,1.0538]

ci_sl = [0.9863,2.1536]

Back to Examples