Commentary on Roger Shepard, and H. B. Barlow, H. Hecht, M. Kubovy, R. Schwartz, and D. Todorovic.
Abstract: 76 words
Main Text: 3140 words
References: 514 words
Acknowledgements: 27 words
Total Text: 3757 words
David H. Foster
d.h.foster@umist.ac.uk
http://www.op.umist.ac.uk/dhf.html
Shepard's analysis of how shape, motion, and color are perceptually represented can be generalized. Apparent motion and shape may be associated with a group of spatial transformations, accounting for rigid and plastic motion. Perceived object color may be associated with a group of illuminant transformations, accounting for the discriminability of surface-reflectance changes and illuminant changes beyond daylights. The phenomenological and mathematical parallels between these perceptual domains may indicate common organizational rules, rather than specific ecological adaptations.
For the biologically relevant properties of objects such as their position, motion, shape, and color, what sorts of representational spaces offer the possibility of yielding invariant psychological principles? The aim here is to show that the analyses Shepard (2001) used to address this problem can be generalized. Thus, the phenomenon of rigid apparent motion between sequentially presented objects may be cast as a special case of more general kinds of apparent motion, and surface color perception under daylights may cast as an invariant of more general illuminant transformations. Supporting experimental data are cited for each. As a side-effect of this generalization, it may be more difficult to maintain the notion that the rules governing these phenomena are specific adaptations to properties of the world (Shepard, 2001), although they remain illuminating (Schwartz, 2001). As with Shepard's approach, the present analysis depends critically on choosing appropriate perceptual representations, here based on the natural group structures of the spaces involved.
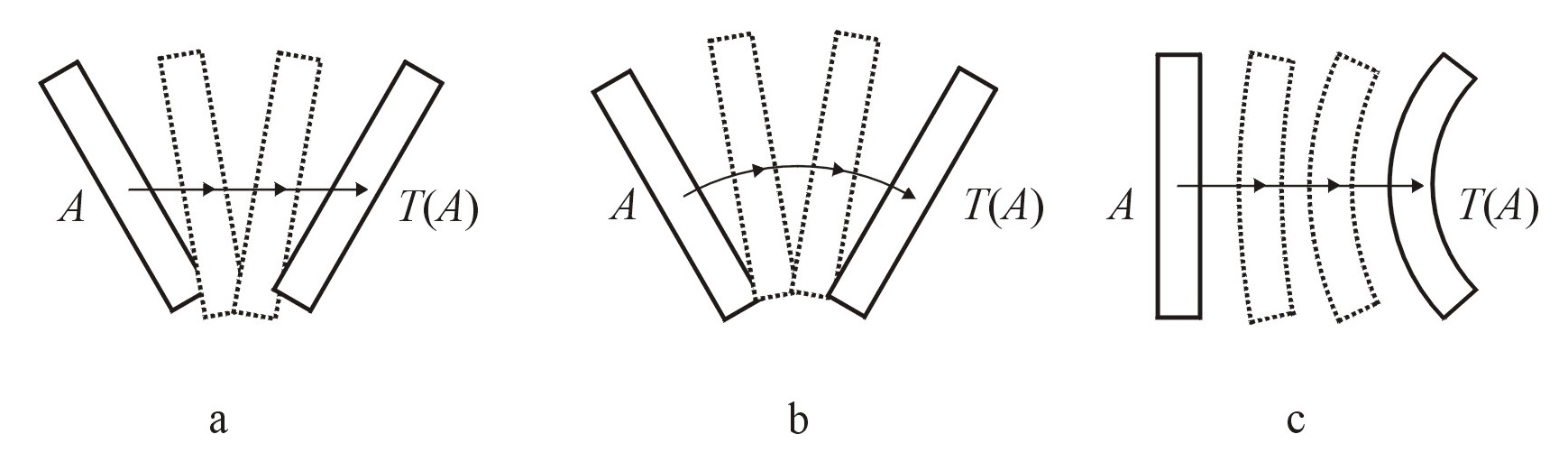
Figure 1a, b shows two possible apparent motion paths between two sequentially presented bars placed at an angle to each other (adapted from Foster, 1978). Of all the possible paths, what determines the one actually perceived? As proposed in Foster (1975b), one way to tackle this problem is to imagine that each path, in some suitable space, has a certain cost or energy associated with it, and, in accord with Maupertius, the path chosen is the one with least energy. As shown later, energy can be defined in two natural ways: (1) with reference to the space in which the object appears to transform; and (2) with reference to the space of transformations acting on the object. Neither is a subcase of the other (cf. Kubovy & Pomerantz, 2001; Todorovic, 2001).

How should apparent-motion paths be described? Assume that a stimulus object A and some transformed version of it T(A) are each defined on a region S of some 2- or 3-dimensional smooth manifold constituting visible space. The spatial transformation T, which describes the point-to-point relationship between A and T(A), should be distinguished from any dynamical process that instantiates this relationship. Depending on the type of apparent motion (rigid or plastic; see Kolers, 1972), an object may change its position, its shape, or both. For the sake of generality, therefore, assume that the transformations T are drawn from a set T that is sufficiently large to allow all such possibilities (Foster, 1978). For technical reasons, assume also that the space S is compact and connected, and that T is a group, with neutral element the identity transformation Id, taking A into itself. Although T is a large group, including nonlinear transformations, it is not assumed to coincide with the entire group of diffeomorphisms of S.
Apparent motion between A and T(A) can then be represented as the generation by the visual system of a time-parameterized family c(t), 0 £ t £ 1, of transformations defining a path in T starting at Id and ending at T; that is, c(0) = Id and c(1) = T. (The actual time scale has been set to unity.)
As shown later, the group T can be given the structure of a Riemannian manifold, so that at each point T of T there is an inner product á , ñ defined on the tangent space at T (the tangent space at a point is simply the collection of all tangent vectors to all possible curves passing through that point). The length ||v|| of a tangent vector v is given by áv, vñ1/2. The length of a path and its (kinetic) energy can then be defined straightforwardly.
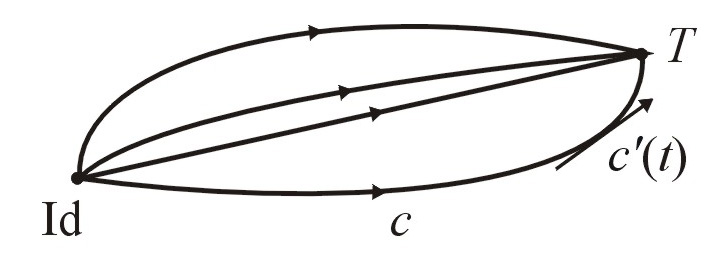
For each path c in the group T of transformations connecting Id to T, its arclength L(c) is given by ò ||c¢(t)|| dt, where c¢(t) is the vector tangent to c at t (i.e. the velocity at c(t); see Fig. 2) and the integral is taken over the interval 0 £ t £ 1. If c, parameterized by arclength, is not longer than any other path with the same start and endpoints, then c is called a geodesic.
The energy E(c) of c is given by ò ||c(t)||2 dt, where the integral is again taken over the interval 0 £ t £ 1. It can be shown that the energy E(c) as a function of c takes its minimum precisely on those paths between Id and T that are geodesics. How, then, should the Riemannian metric || || be defined?
Assume that apparent motion is determined by the properties of the manifold S in which the object appears to transform. As a subset of 2- or 3-dimensional Euclidean space, S inherits the Euclidean metric | |. For a given object A in S, the induced Riemannian metric || || = || ||1 on T is defined thus. Let c¢(t) be the vector tangent to a path c in T at time t (remember that any tangent vector can be represented in this way). As c(t) is a transformation acting on S, it follows that, for each point p in A, the vector (c¢(t))(p) is tangent to the path (c(s))(p), 0 £ s £ 1, at s = t. The energy of A at time t is simply the integral of |(c¢(t))(p)|2 over all p in A. Define ||c¢(t)||1 to be integral of |(c¢(t))(p)| over all p in A.
If T is the group of rigid transformations (isometries) of S, the geodesics produce the types of motion shown in Fig. 1a, where the rotating motion of the bar takes place about its center of mass and the latter moves in a straight line. A matrix formulation is given in Foster (1975b). This is the motion of a free body in space. Yet, as Foster (1975b) and Shepard (2001) pointed out, it is not the apparent motion that is most likely to be observed.
Assume instead that apparent motion is determined by the properties of the group T in which the path is described: the emphasis is thus on transformations rather than transforms. Because T is a group, it has a natural Riemannian metric || || = || ||2, compatible with its group structure, obtained by translating an inner product on the tangent space to T at Id. With respect to || ||2, the geodesics c that pass through Id are (segments of) 1-parameter subgroups of T; that is, c(s + t) = c(s)c(t), wherever they are defined.
If T is the group of rigid transformations of S, the geodesics produce the types of motion shown in Fig. 1b, where the rotating motion of the bar and the movement of the center of mass both take place about the same point. A matrix formulation is given in Foster (1975b). When the perceived paths are estimated by a probe or windowing technique, they are found to fall closer to these "group" geodesics than to those associated with object space, the free-body motions (Foster, 1975b; McBeath & Shepard, 1989; Hecht & Proffitt, 1991).
Shepard's (2001) argument for the simplicity of geodesics concentrated on their representation as rotations or screw displacements in the group of rigid transformations of 3-dimensional space. In fact, their simplicity has a more general basis (Foster, 1975b; Carlton & Shepard, 1990), which, notwithstanding Todorovic (2001), extends to the nonlinear motion shown in Fig. 1c between a straight bar and curved bar, and to non-smooth motion between smooth and non-smooth objects (Kolers, 1972; Foster, 1978). To enumerate: (1) group geodesics minimize energy with respect to the natural metric on the group T; (2) they coincide with the 1-parameter subgroups of T, and are therefore computationally economic in that each may be generated by its tangent vector at the identity Id (Shepard's uniformity principle; see Carlton & Shepard, 1990); and (3) as 1-parameter subgroups each geodesic naturally generates a vector field on S (an assignment of a tangent vector at each point of S varying smoothly from point to point). This assignment does not vary with time; that is, the vector field is stationary. Conversely, a stationary vector field generates a unique 1-parameter subgroup of transformations.
A moving fluid provides a useful example of the significance of stationarity. Its streamlines defined by the velocity vector field usually vary with time, but, if the vector field is stationary, then the streamlines are steady and represent the actual paths of the fluid particles.
In general, the geodesics derived from the natural metric of object space (free-body motions) do not generate stationary vector fields.
The stationarity of vector fields may be relevant to the question of whether kinematic geometry internalizes specific properties of the world (Shepard, 2001). Thus certain vector fields may reflect J. J. Gibson's "ambient optic array" (Shepard, 2001), but they may also relate directly to observers' actions. Some kinds of mental activity, including preparation for movement (Richter et al., 2000) and mental rotation (Deutsch, Bourbon, Papanicolaou, & Eisenberg, 1988), are associated with neuronal activity in the motor cortex and related areas. Each of the vectors constituting a (stationary) vector field could offer the most efficient template for elementary neural activity to take object A into its transform T(A) (see comments by Barlow, 2001). In this sense, apparent motion might be an internalization not of the ways in which objects move freely in space (cf. Hecht, 2001) but of the ways in which observers manipulate or interact with them. Such hypotheses are testable (Barlow, 2001; cf. Kubovy & Epstein, 2001).
The foregoing analysis assumed that the energy of apparent motion is minimized (Foster, 1975b, 1978). Shepard's approach assumed an affine connection (Carlton & Shepard, 1990). The result, however, is the same.
A connection on any manifold M, not necessarily Riemannian, is a rule Ñ that uses one vector field X to transform another vector field Y into a new vector field ÑX(Y). Informally, ÑX(Y) describes how Y varies as one flows along X. In general, even when X and Y are symmetric, ÑX(Y) and ÑY(X) need not coincide, but, if the connection is symmetric, they do.
A connection provides a sensible notion of parallelism with respect to a path c in M. Let Y(t), 0 £ t £ 1, be a parameterized family of vectors such that Y(t) is in the tangent space to M at c(t). Then Y is said to be parallel with respect to c if Ñc¢(Y)c(t) = 0 for all t. With respect to this connection, a path c is called a geodesic if the family of tangent vectors c¢(t) is parallel with respect to c.
Now suppose that the manifold M has a Riemannian metric. A connection Ñ on M is compatible with the Riemannian metric if parallel translation preserves inner products; that is, for any path c and any pair X, Y of parallel vector fields along c, the inner product áX, Yñ is constant. According to the fundamental theorem of Riemannian geometry, there is one and only one symmetric connection that is compatible with its metric: the Levi-Civita connection.
The geodesics defined as length-minimizing paths in the group T of transformations are therefore precisely the same as the geodesics defined with respect to the Levi-Civita connection on T. The premiss adopted by Shepard (2001) and Carlton & Shepard (1990) is therefore formally equivalent to that in Foster (1975b).
A problem with geodesic-based schemes for apparent motion—whether based on metrics or connections—is how to cost the degree to which object structure is preserved. As Kolers (1972) and others have noted, if the rigid transformation T relating two objects is sufficiently large, then the apparent motion may become non-rigid or plastic, even if T has not reached a cut point on the geodesic (e.g. an antipodal point on the sphere).
One way to accommodate this failure is to introduce an additional energy function E1 that represents the cost of preserving metric structure over a path. Such a notion is not implausible. In shape-recognition experiments with stimulus displays too brief to involve useful eye movements or mental rotation, performance is known still to depend strongly on planar rotation angle (see e.g. Foster, 1991). Thus, for a rigid transformation T far from Id, the total energy of the geodesic c connecting Id and T would be ò ||c¢(t)||2 dt + E1(c), which could exceed the energy ò ||b¢(t)||2 dt + E2(b) of some other, longer path b connecting Id and T, preserving a weaker non-metric structure with smaller energy function E2.
If this is true, there ought to be a close relationship between apparent motion and visual shape recognition.
The existence of rigid apparent motion between two objects implies that a visual isometry can be established. In a shape-recognition experiment, therefore, the two objects should be recognizable as each other. This hypothesis has been confirmed for rotated random-dot patterns (Foster, 1973). But how should one deal with structures other than metric ones? In practice, one needs a definition of structure that can be interpreted operationally in terms of the transformations (isomorphisms) preserving that structure (Foster, 1975a; Van Gool, Moons, Pauwels, & Wagemans, 1994). For (1) metric, (2) affine, (3) projective, and (4) topological structures, their groups of isomorphisms form a nested sequence, T1ÌT2ÌT3ÌT4 . Accordingly, for one of these more general structures i, suppose that transformation T is drawn from Ti and that sequentially presenting object A and transform T(A) produces apparent motion that lies entirely within Ti. Then, in a shape-recognition experiment, A and T(A) should be recognizable as each other with respect to the structure i. Such an exercise offers the possibility of identifying an underlying structure for visual space (Foster, 1975a; Indow, 1999).
The remainder of this commentary is concerned with perceived surface color, which can be analyzed in a somewhat similar way to apparent motion.
The illumination on surfaces varies naturally, and the spectrum of the light reaching the eye depends both on the reflectance function of the surface and on the illuminant spectrum. Shepard (2001) suggested that the intrinsically 3-dimensional nature of daylights is intimately linked to how observers compensate for illuminant variations.
Yet the degree to which observers are color constant is limited, with levels in the unadapted eye rarely exceeding 0.6–0.7, where on a 0–1 scale 1.0 would be perfect constancy (for review, see Foster, Amano, & Nascimento, 2001). In contrast, observers can rapidly, effortlessly, and reliably discriminate illuminant changes on a scene from simultaneous changes in the reflecting properties of its surfaces (Craven & Foster, 1992). The sequential presentation of the stimuli generates a strong temporal cue: illuminant changes give a "wash" over the scene and reflectance changes a "pop-out" effect (Foster et al., 2001). The former is analogous to apparent motion between an object and its smooth transform, and the latter to split apparent motion between an object and its discontinuous transform.
If perceived surface color is not always preserved under illuminant changes, then what is invariant in discriminations of illuminant and material changes?
One possibility is that observers assess whether the perceived relations between the colors of surfaces are preserved, that is, whether relational color constancy holds. Relational color constancy is similar to color constancy but refers to the invariant perception of the relations between the colors of surfaces under illuminant changes. It has a physical substrate in the almost-invariant spatial ratios of cone excitations generated in response to light, including lights with random spectra, reflected from different illuminated surfaces (Foster & Nascimento, 1994). There is strong evidence that observers use this ratio cue, even when it may not be reliable (Nascimento & Foster, 1997).
In the language of geometric-invariance theory, relational color constancy is a relative invariant with respect to illuminant changes, and, in that sense, is a weaker notion than color constancy (Maloney, 1999). But relational color constancy can be used to produce color-constant percepts. Again, the argument depends on group properties.
The set T of all illuminant transformations T is a one-to-one copy of the multiplicative group of (everywhere-positive) functions defined on the visible spectrum, and it accordingly inherits the group structure of the latter. The group T induces (Foster & Nascimento, 1994) a canonical equivalence relation on the space C of all color signals (each signal consisting of the reflected spectrum at each point in the image). That is, C1 and C2 in C are related if and only if T(C1) = C2 for some T in T.
The assumption of color constancy is that it is possible to find some f that associates with each C in C a percept f(C) that is invariant under illuminant transformations. Because T is a group, there is a one-to-one correspondence between color-constant percepts f(C) and equivalence classes [C] of illuminant-related color signals. This formal equivalence between color constancy and relational color constancy can be exploited in practical measurements (e.g. Foster et al., 2001).
As Shepard (2001) pointed out, although we may not perceive everything that could be perceived about each surface, we at least perceive each surface as the same under all naturally occurring conditions of illumination, and, as argued here, sometimes even under unnatural illuminants.
The representations of apparent motion and perceived shape and object color are intimately associated with groups of spatial transformations. In Shepard's analysis, the geodesics for apparent motion are attributed to an affine connection, but the same geodesics can be derived as the natural energy-minimizing paths of a transformation group, which allows an additional energy function to be introduced to accommodate rigid-motion breakdown, and more generalized kinds of shape recognition. In Shepard's analysis of perceived object color, daylight illuminants have a special role, but the same perceptual invariants may be obtained with groups of illuminant transformations beyond the daylight locus.
What of the evidence? For rigid transformations in 2- and 3-dimensional space there is a clear bias towards motions following the natural transformation-group metric. There is also evidence that rigid apparent motion does not occur at angles of rotation where shape recognition does not occur, consistent with the proposed link between the two phenomena. Finally, there is evidence that observers can exploit violations of invariance of spatial color relations under illuminant transformations in a predictable way.
The phenomenological and mathematical parallels between these various perceptual domains may not be consequences of Shepard's notion of adaptation to specific properties of the world. They do, however, suggest an application of common organizational rules.
Barlow, H. B. (2001). The exploitation of regularities in the
environment by the brain. Behavioral and Brain Sciences,
24(3), XXX-XXX.
Carlton, E. H., Shepard, R. N. (1990). Psychologically simple
motions as geodesic paths. I. Asymmetric objects. Journal of
Mathematical Psychology, 34, 127-188.
Craven, B. J., Foster, D. H. (1992). An operational approach
to colour constancy. Vision Research, 32, 1359-1366.
Deutsch, G., Bourbon, W. T., Papanicolaou, A. C., Eisenberg,
H. M. (1988). Visuospatial Tasks compared via activation of regional
cerebral blood-flow. Neuropsychologia, 26(3), 445-452.
Foster, D. H. (1973). An experimental examination of a hypothesis
connecting visual pattern recognition and apparent motion. Kybernetik,
14, 63-70.
Foster, D. H. (1975a). An approach to the analysis of the underlying
structure of visual space using a generalized notion of visual
pattern recognition. Biological Cybernetics, 17,
77-79.
Foster, D. H. (1975b). Visual apparent motion and some preferred
paths in the rotation group SO(3). Biological Cybernetics,
18, 81-89.
Foster, D. H. (1978). Visual apparent motion and the calculus
of variations. In E. L. J. Leeuwenberg B. H. F. J. M. (Eds.),
Formal Theories of Visual Perception (pp. 67-82). Chichester:
Wiley.
Foster, D. H., Amano, K., Nascimento, S. M. C. (2001). How
temporal cues can aid colour constancy. Color Research and
Application, 26 (suppl.), S180-S185.
Foster, D. H., Nascimento, S. M. C. (1994). Relational colour
constancy from invariant cone-excitation ratios. Proceedings
of the Royal Society of London, Series B, 257, 115-121.
Hecht, H. (2001). Regularities of the physical world and the
absence of their internalization. Behavioral and Brain Sciences,
24(3), XXX-XXX.
Hecht, H., Proffitt, D. R. (1991). Apparent extended body motions
in depth. Journal of Experimental Psychology: Human Perception
and Performance, 17(4), 1090-1103.
Indow, T. (1999). Global structure of visual space as a united
entity. Mathematical Social Sciences, 38(3), 377-392.
Kolers, P. A. (1972). Aspects of motion perception. Oxford: Pergamon.
Kubovy, M. (2001). Internalization: A metaphor we can live
without. Behavioral and Brain Sciences, 24(3), XXX-XXX.
Maloney, L. T. (1999). Physics-based approaches to modeling
surface color perception. In K. R. Gegenfurtner L. T. Sharpe (Eds.),
Color Vision: From Genes to Perception (pp. 387-416). Cambridge:
Cambridge University Press.
McBeath, M. K., Shepard, R. N. (1989). Apparent motion between
shapes differing in location and orientation: A window technique
for estimating path curvature. Perception Psychophysics,
46(4), 333-337.
Nascimento, S. M. C., Foster, D. H. (1997). Detecting natural
changes of cone-excitation ratios in simple and complex coloured
images. Proceedings of the Royal Society of London, Series
B, 264, 1395-1402.
Richter, W., Somorjai, R., Summers, R., Jarmasz, M., Menon,
R. S., Gati, J. S., Georgopoulos, A. P., Tegeler, C., Ugurbil,
K., Kim, S. G. (2000). Motor area activity during mental rotation
studied by time- resolved single-trial fMRI. Journal of Cognitive
Neuroscience, 12(2), 310-320.
Schwartz, R. (2001). Evolutionary internalized regularities.
Behavioral and Brain Sciences, 24(3), XXX-XXX.
Shepard, R. N. (2001). Perceptual-cognitive universals as reflections
of the world. Behavioral and Brain Sciences, 24(3),
XXX-XXX.
Todorovic, D. (2001). Is kinematic geometry an internalized
regularity? Behavioral and Brain Sciences, 24(3),
XXX-XXX.
Van Gool, L. J., Moons, T., Pauwels, E., Wagemans, J. (1994).
Invariance from the Euclidean geometer's perspective. Perception,
23, 547-561.
This work was supported by the Engineering and Physical Sciences Research Council. I thank E. Pauwels for helpful discussions and E. K. Oxtoby for critically reading the manuscript.