I am currently seeking to recruit PhD student to work with me and Prof. Anne Juel on a PhD project (fully funded for UK/EU students), focusing on experiments in nonlinear dynamics. The advertisement for this project is given below. I would be very happy to discuss the project or PhD position by email, phone or video conference with anyone who is interested.

Applications are sought for a PhD project associated with a recently-funded EPSRC project (Feedback Control of Deformable Bubbles), to use new control-based experimental methods to explore and stabilise disordered multiphase flows. This interdisciplinary, self-contained experimental PhD project draws on aspects of nonlinear dynamics, control theory, fluid dynamics and soft matter and offers the opportunity for the successful applicant to interact closely with a PDRA in the Department of Mathematics tasked with developing the theoretical control framework.

The PhD student will be supervised by Dr. Alice Thompson (alice.thompson@manchester.ac.uk, Department of Mathematics) and Prof. Anne Juel (anne.juel@manchester.ac.uk, Department of Physics and Astronomy).

We study the propagation of an air bubble through a confined fluid-filled channel (a Hele-Shaw cell; see Fig. 1a) -- a prototypical nonlinear system exhibiting an abrupt transition to disorder and amenable to both controlled experiments and numerical simulations using a simplified model. At low flow rates, the bubble propagates steadily and is insensitive to unavoidable background perturbations in the channel. This so-called invariant state of the system is therefore stable, in accordance with model predictions. Unstable invariant modes of bubble propagation are also predicted by the model (Fig. 1b), but cannot be observed in the experiments other than transiently (Fig. 1c).

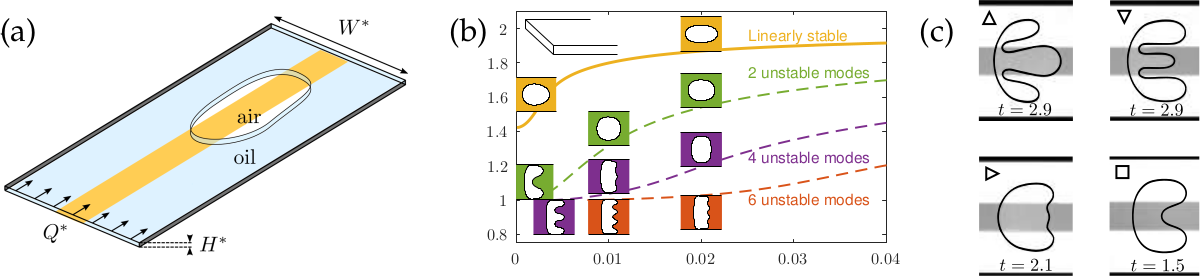
Figure 1: (a) A bubble confined in a Hele-Shaw cell, (b) theoretical predictions for stable and unstable steady propagation modes, and (c) experimental snapshots of evolving bubbles suggesting that the bubble transiently adopts unstable configurations similar to those in (b).

Above a threshold value of the flow rate (dependent on the level of background perturbations), the bubble motion abruptly becomes disordered in that the bubble propagates with irregular speed and exhibits complex shape changes. This complex dynamics has been conjectured to be organised by weakly unstable invariant states of the system so that the bubble transiently `adopts' different unstable configurations.

The aim of this project is to use new control methods to explore the dynamics of static and propagating confined bubbles. Our main goal is to use feedback control to detect and stabilise the underlying unstable modes, with a second aim of using control to deliver precise perturbations to probe the transition to disorder in the uncontrolled system. Importantly, observations of both stable and unstable regimes can be based entirely on experiments, without relying on costly or inaccurate theoretical models. Such new capabilities will enable improved understanding of how disordered systems operate, and are likely to have applications in a wide range of fluid and soft matter research.

Laboratory experiments will be hosted within the Manchester Centre for Nonlinear Dynamics, and the funding for this project includes a generous budget for consumables.

The successful candidate should have experience (or strong interest) in experiments, and a good undergraduate/masters degree in applied mathematics, physics or engineering.

Dedicated funding for this project is available via the Department of Mathematics, which will cover fees and stipend for UK candidates. Other students should enquire about alternative funding availability.