Airway Closure: Static Liquid Bridges in Non-Axisymmetrically
Buckled Elastic Tubes
Background
The lung's airways are coated with a thin liquid film which affects
many aspects of its mechanical behaviour. In the smaller airways
where the wall curvature is large, the surface tension
of the liquid film is important and is generally believed to be
the cause of `airway closure' which has been observed directly
and indirectly in the excised lungs of laboratory animals.
Airway
closure occurs through
the
formation of occluding liquid bridges across the airway lumen.
The formation of these liquid bridges is assumed to follow the growth of a
Rayleigh instability of the liquid lining which is commonly referred to
as `film collapse'. The formation of the liquid bridge can be
accompanied (and indeed dominated) by large elastic
deformations of the airway walls, leading to a so-called `compliant collapse'.
The physiological problems associated with airway closure are greatly
enhanced in prematurely born babies whose lungs cannot produce
sufficient quantities of the surfactant which reduces the liquid
film's surface tension. This manifests itself in the potentially
life-threatening `Respiratory Distress Syndrome'.
The Problem
Previous
theoretical investigations of this problem were restricted to axisymmetric geometries.
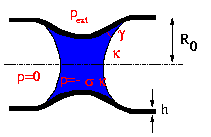
In the study presented here, we examine if the compressive force that
the liquid bridge exerts on the airway wall is strong enough to make
the airway buckle non-axisymmetrically. This would have important
implications since
much smaller volumes of fluid are required to form an occluding liquid
bridge in a non-axisymmetrically collapsed airway than in an
axisymmetric one. The volume of
fluid required to form a `minimal liquid bridge' in a
non-axisymmetrically buckled tube is therefore an important parameter
to be determined in this study.
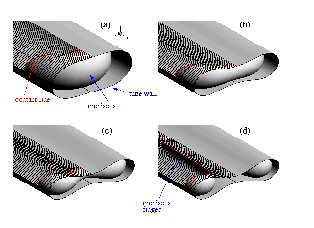
II. Minimal liquid bridges for zero surface tension.
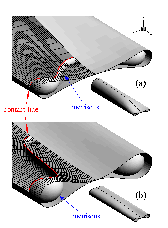
III. Minimal liquid bridges for finite surface tension.
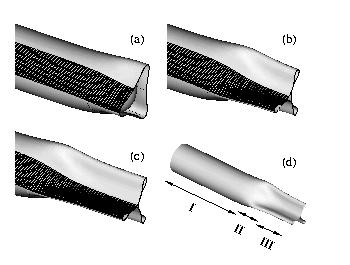
IV. Opposite wall contact and higher buckling modes.
V. Conclusions.
Page last modified: September 29, 2000
Back to Matthias Heil's home page..

